应用时间序列分析（王燕）学习笔记2

时间序列的预处理

拿到一个观察序列后，首先要对它的平稳性和纯随机性进行检验，这两个重要的检验称为序列的预处理。根据检验的结果可以将序列分为不同的类型，对不同的类型我们采用不同的分析方法。

2.1 平稳性检验

特征统计量：平稳性是某些时间序列具有的一种统计特征。要描述清楚这个特征，我们必须借助如下统计工具：

1. 概率分布
2. 一个更简单的、更实用的描述时间序列统计特征的方法是研究该序列的低阶矩，特别是均值、方差、自协方差和自相关系数，它们也被称之为特征统计量。
   尽管这些特征统计量不能描述随机序列全部的统计性质，但由于它们概率意义明显，易于计算，而且往往能代表随机序列的主要概率特征，所以我们对时间序列进行分析，主要就是通过分析这些特征量的统计特性，推断出随机序列的性质。
   1.均值
   2.方差
   3.自协方差函数（autocovariance function）和自相关系数（autocorrelation coefficients）

通常的协方差函数和自相关系数度量的是两个不同事件彼此之间的相互影响程度，而协方差函数和自相关系数度量的是同一事件在两个不同时期之间的相关程度，形象地讲就是度量自己过去的行为对自己现在的影响。

平稳时间序列的定义
根据限制条件的严格程度，分为严平稳时间序列和宽平稳时间序列
一、严平稳（strictly stationary）
就是一种条件比较苛刻的平稳性定义，它认为只有当序列所有的统计性质都不会随着时间的推移而发生变化时，该序列才被认为平稳。随机变量族的统计性质由它们的联合概率分布族决定
严平稳时间序列通过只有理论意义，在实践中更多的是条件比较宽松的平稳时间序列。
二、宽平稳（week stationary）
使用序列额特征统计量来定义一种平稳性。它认为序列的统计性质主要由它的低阶矩决定，所以只要保证序列低阶平稳（二阶），就能保证序列的主要性质近似稳定。
宽平稳也称为若平稳或二阶平稳（second-order stationary）
显然，严平稳比宽平稳条件严格。严平稳是对序列联合分布的要求，以保证序列所有的统计特征都相同；而宽平稳只要求序列二阶平稳，对于高于二阶的矩没有任何要求。所以通常情况下，严平稳序列也满足宽平稳条件，而宽平稳序列不能反推平稳成立。
但这不是绝对的，两种情况都有特例。
比如服从可惜柯西分布的严平稳序列就不是宽平稳序列，因为它不存在一、二阶矩，所以无法验证它二阶平稳。严格地讲，只有存在二阶矩的严平稳序列才能保证它一定也是宽平稳序列。
在实际应用中，研究中最多的是宽平稳随机序列，以后见到平稳随机序列，如果不加特殊注明，指的都是宽平稳随机序列。如果序列不满足平稳条件，就称为非平稳序列。
平稳时间序列的统计性质
一、常数均值
二、自相关系数的三个性质：

1. 规范性
2. 对称性
3. 非负性
   一个平稳时间序列一定唯一决定了它的自相关函数，但一个相关函数未必唯一对应着一个平稳时间序列。
   时间序列分析方法作为数理统计学的一个专业分支，它遵循数数理统计学的基本原理，都是利用样本信息来推测总体信息。
   根据数理统计学 常识，显然要分析的随机变量越少越好，而每个变量获得样本信息越多越好。随机变量越少，分析的过程就越简单，而样本容量越大，分析的结果就越可靠。
   平稳性的检验
   一种是根据时序图和自相关图显示的特征做出判断的图检验方法；一种是构造检验统计量进行假设检验的方法。
   图检验是一种操作简便，运用广泛的平稳性判别方法，它的缺点是判别结论带有很强的主观色彩。所以最好能用统计检验的方法加以辅助判断。目前最常用的平稳性检验方法是单位根检验（unit root test）。
   一、时序图检验
   根据平稳时间序列均值、方差为常数的性质，平稳序列的时序图应该显示出该序列始终在一个常数附近随机波动，而且波动的范围有界的特点。如果观察序列的时序图显示出有明显的趋势性或周期性，那它通常不是平稳序列。
   

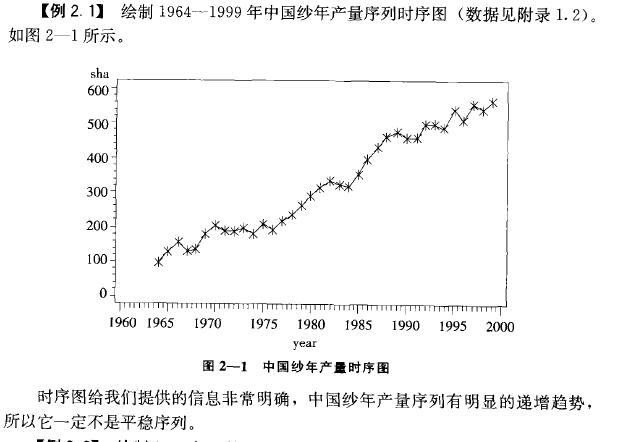
平稳序列的例子

自相关图检验
平稳序列具有短期相关性。

纯随机性检验
拿到一个观察值序列后，首先是判断它的平稳性。通过平稳性检验，序列可以分为平稳序列和非平稳序列。
对于非平稳序列，由于它不具有二阶矩平稳的性质，所以对它的统计分析要周折一些，通常要进行进一步的检验、变换或处理之后，才能确定适当的拟合模型。
如果序列平稳，情况就简单多了，我们有一套非常成熟的平稳序列建模方法。但是，并不是所有的平稳序列都值得建模。只有那些序列值之间具有密切的相关关系，历史数据对未来的发展有一定影响的序列，才值得我们花时间去挖掘历史数据中的有效信息，用来预测序列未来的发展。
如果序列值彼此之间的任何相关性，那就意味着该序列是一个没有记忆的序列，过去的行为对将来的发展没有任何的影响，这种序列我们称之为纯随机序列。从统计分析的角度而言，纯随机序列是没有任何分析价值的序列。

白噪声序列的性质
一、纯随机性
二；方差齐性：序列中每个变量的方差都相等。如果序列不满足方差齐性，就称该方差具有异方差性质。
在时间序列分析中，方差齐性是一个非常重要的限制条件。因为根据马尔可夫**定理，只有方差齐性假定成立，我们用最小二乘法得到的未知参数估计值才是准确的、有效的。如果假定不成立，最小二乘估计值就不是方差最小线性无偏估计，拟合模型的预测精度会受到很大影响。
所以我们在进行模型拟合时，检验内容之一就是要检验拟合模型的残差是否满足方差齐性假定。如果不满足，那就说明残差序列还不是白噪声序列，即拟合模型没有充分提取随机序列中的相关信息，这时拟合模型的精度是值得怀疑的。这种场合下，我们通常需要使用适当的条件异方差模型来拟合该序列的发展。**
纯随机性检验

Q统计量

LB统计量
LB统计量实际上是Box和Pierce的Q统计量的修正，所以人们习惯上把它们统称为Q统计量，分别记作Q_bp统计量和Q_lb统计量。在各种检验场合普遍采用的Q统计量通常指的是LB统计量。

下一章详细介绍这种平稳非白噪声序列的建模及预测方法。

---

使用gplot程序来绘制时序图

data example2_1;                                                                                                                        
input price1 price2;                                                                                                                    
time=intnx('month','01jul2004'd,_n_-1);                                                                                                 
format time date.;                                                                                                                      
cards;                                                                                                                                  
12.85 15.21                                                                                                                             
13.29 14.23                                                                                                                             
12.41 14.69                                                                                                                             
15.21 13.27                                                                                                                             
14.23 16.75                                                                                                                             
13.56 15.33                                                                                                                             
 ;                                                                                                                                      
proc gplot data=example2_1;                                                                                                             
plot price1*time=1 price2*time=2/overlay;                                                                                               
symbol1 c=black v=star i=join;                                                                                                          
symbol2 c=red v=circle i=spline;                                                                                                        
run;                                                                                                                                    
proc print data=example2_1;                                                                                                             
run;

平稳性和纯随机性检验
一、平稳性检验
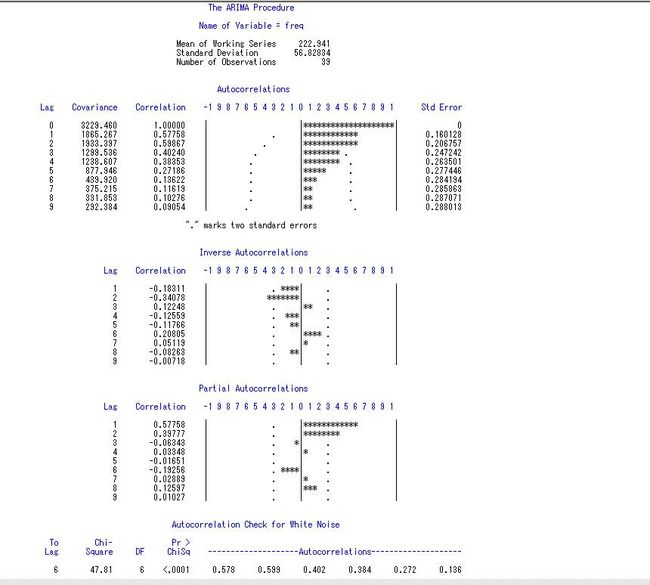
为了判断序列是否平稳，除了需要考查时序图的性质，还需要对自相关图进行检验。SAS系统ARIMA过程中的IDENTIFY语句可以提供非常醒目的自相关图。

data example2_2;                                                                                                                        
input freq@@;                                                                                                                           
year=intnx('year','1jan1970'd,_n_-1);                                                                                                   
format year year4.;                                                                                                                     
cards;                                                                                                                                  
97 154 137.7 149 164 157 188 204 179 210 202 218 209                                                                                    
204 211 206 214 217 210 217 219 211 233 316 221 239                                                                                     
215 228 219 239 224 234 227 298 332 245 357 301 389                                                                                     
;                                                                                                                                       
proc arima data=example2_2;                                                                                                             
identify var=freq;                                                                                                                      
run;