HDU/HDOJ 1232 超详细题解（并查集入门教程）

题目链接：http://acm.hdu.edu.cn/showproblem.php?pid=1232

 

HDU1232这道题属于并查集

 

思路：

 

城市之间由道路连接，相连的城市可以看做一个集合，如：a、b相连，c、d相连，则a和b属于集合A，c和d属于集合B。之后又有人告诉你b和e相连，那么就把e加入到集合A中，以此类推。然后不同集合若是想组成一个大的集合，即集合A和集合B若相连接在一起，那随便在两个集合中分别找两个城市连接在一起就可以了。

 

在这里稍微讲解一下并查集，并查集一般由一个整形数组和两个函数构成，其中数组pre[x]记录的是x的前导节点，若把并查集中的节点看做数的话，那pre[x]数组中记录的就是x的父节点。

 

大家都知道树有个根节点，我们把集合A和集合B分别看成两棵树，每棵树上的节点都可以互相连接，那任意给我两个节点我怎样才能分辨是否相连通呢?我们就可以判断他的根节点是什么，若根节点相同，说明两个节点都属于集合A（或集合B）并且可以连通。

 

所以可以通过find函数来寻找某节点的根节点：

 

int find (int x){
	int r;//r代表的是根节点
	while(pre[r]!=r){//根节点的pre存的是它自己
		r=pre[r];
}
return r;
}

题目中给我们的是x,y两个城市的编号，告诉我们他们可以连接，那我们如何用代码来体现呢？

 

我们可以写一个join函数，用于把x,y加入到某个集合中去，证明他们能连通。

 

可以通过修改x或y根节点的前导数组pre来实现：

int join(int x,int y){
	int r_x=find(x),r_y=find(y);//寻找到x和y的根节点，判断x,y是否连通
	if(r_x!=r_y){//若两者的根节点相同就不用执行了
		//让x的根节点的前导改为y节点的根节点，相当于把x和y所在的树合并成一颗树。这样x,y在树中连通。
		pre[r_x]=r_y;//这里也可以写成pre[r_y]=r_x,只要把x,y的根节点改成一样就行了
	}
}

优化：

大家想想还有没有什么优化方法？

 

当然是有的，若是经常判断某两个节点的根节点是什么，每次都要执行一次find里面的循环，有没有觉得很浪费？我们明明找一次根节点就行了。

 

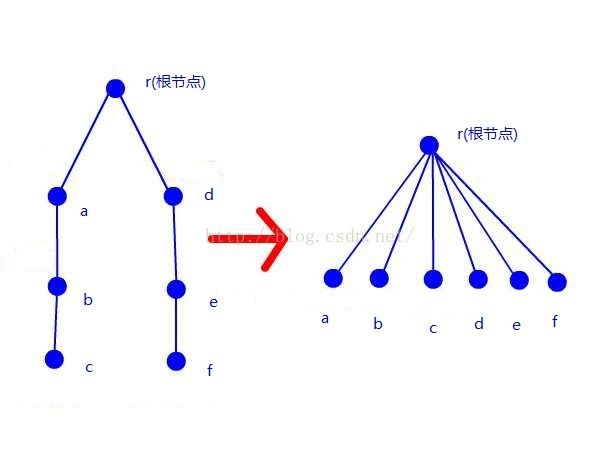
看图：

这样的话找f的根节点的时候直接找pre[f]就行了，不用每次遍历一次，一次修改，终身受用。

 

所以find函数可以改成这样：

int find(int x){
    int r=x;
    while(pre[r]!=r){
        r=pre[r];
    }
    //找到根节点r之后，把这棵树的所有节点的前导全部改为r这样就不用每次都上探寻找一次根节点了
    int i=x,j;//j是个临时变量，存放i的前导
    while(i!=r){//一直执行到根节点
        j=pre[i];
        pre[i]=r;
        i=j;
    }//把经过的节点的前导全改成r
    return r;
}

这个方法专业点的叫法是——路径压缩。

 

还有个注意的地方，就是开始必须初始化所有的节点的前导都是自己，也就是pre[x]=x;

 

好了，分析过程都讲完了，贴个完整的代码：

 

#include 
#include 
#include 
int pre[1010];

int find(int x){//查找并返回某个节点的根节点
    int r=x;//根节点root
    while(pre[r]!=r){
        r=pre[r];
    }
    int i=x,j;
    while(i!=r){//路径压缩，让所有节点的pre直接指向根节点
        j=pre[i];
        pre[i]=r;
        i=j;
    }
    return r;
}

void join(int x,int y){
    int r_x=find(x),r_y=find(y);
    if(r_x!=r_y){
        pre[r_x]=pre[r_y];
    }
}

int main()
{
    int hash[1010];
    int n,m,i,x,y,sum;
while(scanf("%d%d",&n,&m)&&n){
	 //初始化
        sum=0;
        memset(hash,0,sizeof(hash));
        for(i=1;i<=n;i++){
            pre[i]=i;
        }

        while(m--){
            scanf("%d%d",&x,&y);
            join(x,y);
        }

        for(i=1;i<=n;i++){
            hash[find(i)]=1;
        }
        for(i=1;i<=n;i++){
            sum+=hash[i];
        }
        printf("%d\n",sum-1);
    }
    return 0;
}