UPC 2020年夏混合个人训练第七十五场

问题 A: building

时间限制: 1 Sec 内存限制: 128 MB

题目描述
WOW是BLIZZARD公司开发的一款网络游戏，游戏的背景是处在一个叫做艾泽拉斯的神秘大陆上的。在这片陆地上生活着许多不同种族不同部落的奇幻生物，暗夜精灵就是其中的一员。他们拥有高深的科技和强大的魔法，但却因为性格的冷傲孤僻而不被其他种族所接受。为了改善这种状况，半神塞纳留斯决定发展有暗夜精灵族特色的产业来吸引外族，他发现暗夜精灵的建筑风格深受世人青睐，因为它们都是古树的造型，且具有一种神奇的魔力，就是在占地面积不变的情况下可以自由改变形状，使得建筑之间完全没有空隙。
于是，他将这一艰巨的任务交给了部落中最具天赋的工程师守望者玛维，让他在一块面积为n（0<=n<=100）的土地上建造若干个建筑，这些建筑都有各自的占地面积q(0<=q<=100)，价格p(0<=w<=100)和魅力值v(0<=v<=100)。就暗夜精灵当前掌握的科技来看，他们可以建造m(0<=m<=100)种建筑，为了不使游客感到乏味，每一种建筑规定最多只能建一座。
你的任务就是替玛维想出一种选择建造的方案，使得最多用k(0<=k<=100)的金钱，在面积为n的土地上建出的建筑具有最高的魅力值。

输入
第一行有三个数m,n,k;以下有m行，分别包含了m种建筑的占地面积q，价格p和魅力值v。
输出
仅有一个数，为最高魅力值。
样例输入
5 12 11
4 3 3
3 2 6
2 4 2
6 3 7
5 5 6
样例输出
15

这是一条较为典型的背包DP，详见代码

#include 
#define MAXNUM 101
#define MAX(a,b) a>b?a:b
 
int m;			//建筑的种类数 
int n;   		//土地的面积   
int k;			//使用的金钱数 
int q[MAXNUM];  //建筑i的占地面积 
int p[MAXNUM];  //建筑i的价格
int v[MAXNUM];	//建筑i的魅力值 
int f[MAXNUM][MAXNUM];  //f表示前i个获得的最大魅力值 
 
int main()
{
	scanf("%d%d%d",&m,&n,&k);
	for(int i=1; i<=m; i++)
		scanf("%d%d%d",&q[i],&p[i],&v[i]);
		
	memset(f,0,sizeof(f)); 
	for(int i=1; i<=m; i++)
		for(int j=n; j>=1; j--)
			for(int h=k; h>=1; h--)
				if(j<q[i]||h<p[i])  f[j][h]=f[j][h];
				else  f[j][h] = MAX(f[j][h], f[j-q[i]][h-p[i]]+v[i]);
	printf("%d\n",f[n][k]);
	return 0;
} 

问题 B: Ferry

时间限制: 1 Sec 内存限制: 128 MB

题目描述
iRabbit的国家被一条河流(河流是直的)分成南北两岸，南北两岸各有N个城市。北岸的每一个城市有一个唯一的友好城市在南岸，且他们的友好城市彼此不同。为了城市关系的发展，每对城市之间都想要开通轮渡。由于河面上常常有雾，并且水速很快。iRabbit决定禁止船只航线相交。以避免发生安全事故。 iRabbit希望能在保证安全的情况下，尽可能多地开通航线。由于N非常大，所以必须用程序解决。iRabbit因为备战竞赛，所以十分繁忙，没有时间来编写程序，所以交给手下的TCR和sceoy解决。可是他们两个想了很久都没有想出答案，所以想请你来帮助解决。

输入
每组数据第一行有两个整数：N（1≤N≤100000）、河的长度M(longint) 接下来N行，每行两个数A、B。表示这一对友好城市与河源头的距离（A代表北岸城市、B代表南岸城市），每一确定位置只可能有一座城市。
输出
每组数据每行输出一个整数。表示可以开通轮渡的最大线路数线路数。
样例输入
7 30
22 4
2 6
10 3
15 12
9 8
17 17
4 2
样例输出
4

O(n^2)的朴素DP做法

#include
using namespace std;
const int MAX = 2e5+10; 

struct node{int X1,X2;} line[MAX];
int n,f[MAX],ans;

bool cmp(const node &a,const node &b){
	return a.X1<b.X1;
}

int main()
{
	scanf("%d",&n);
	for(int i=1; i<=n; i++) 
	    scanf("%d %d",&line[i].X1,&line[i].X2);
	    
	sort(line+1,line+n+1,cmp);
	for(int i=1; i<=n; i++)  f[i]=1;
	
	for(int i=2; i<=n; i++)
		for(int j=1; j<=i-1; j++)
			if(line[j].X2 < line[i].X2) 
			    f[i] = max(f[i],f[j]+1);
		
	for(int i=1; i<=n; i++) 
	    ans=max(ans,f[i]);
	    
	cout<<ans;
	return 0;
}

这样的复杂度是过不了的，我们需要继续分析问题，回归到问题的本质。把这些城市的南岸城市（北岸也可以）坐标从小到大排好序后，我们分析一下选择哪些北岸城市的坐标可以构成“合法航线”，参考下图：

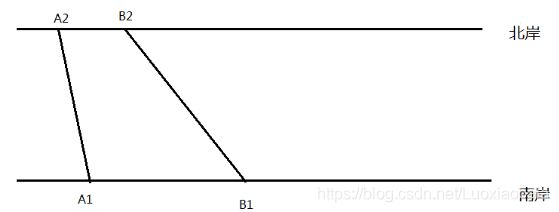
可以发现： 当A1A2(A1让北岸的坐标构成一个最长上升子序列。因此，这题的本质就是：用O(nlogn)做法求最长上升子序列(LIS)的长度。 代码中使用了一个二分查找函数：lower_bound( )。

#include
using namespace std;
const int MAX = 2e5+10; 

struct node {int X1,X2;} line[MAX];
int n,f[MAX],t[MAX],cnt,m;

bool cmp(const node &a,const node &b) {return a.X1<b.X1;}

int main()
{
	scanf("%d %d",&n,&m);
	for(int i=1;i<=n;i++) 
	    scanf("%d %d",&line[i].X1,&line[i].X2);
	sort(line+1,line+n+1,cmp);
	
	t[++cnt]=line[1].X2;
	
	for(int i=2;i<=n;i++)
	{
		int tmp=lower_bound(t+1,t+cnt+1,line[i].X2)-t;
		if(tmp<=cnt)  t[tmp]=line[i].X2;
		else  t[++cnt]=line[i].X2;
	}
	cout<<cnt;
	return 0;
}

问题 D: 找小行星很容易吗 (mira)

时间限制: 1 Sec 内存限制: 128 MB

题目描述
为了给小行星赋予自己姬友的名字（Ao），木之幡米拉 (Konohata Mira) 决定找到一颗新的小行星。
为了更加方便的寻找小行星，她把决定把星空划分为一个 n 行 m 列的方格图，方阵中一共有 n*m 个正方形，你可以认为每个正方形都是全等的。
为了更加方便的寻找小行星，她认为这个方格图中的任意一个矩形为一个区域。
为了更加方便的寻找小行星，她希望求出每个区域的小行星数量。
为了更加方便的寻找小行星，她想让你算出这个方格图中的区域数量 s ，剩下的事情交给她和真中苍 (Manaka Ao) 就行了。
为了更加方便的寻找小行星，你只需要求出 s mod 998244353 的值即可。

输入
输入共包括一行两个整数n,m，分别表示这个方阵的行数和列数。
输出
输出共包括一行一个整数，分别表示这个方阵的区域个数 s mod 998244353 的值。
样例输入
2 3
样例输出
18
提示
样例解释:
图自己画。
1×1 的方格有 6 个。
1×2 的方格有 7 个。
1×3 的方格有 2 个。
2×2 的方格有 2 个。
2×3 的方格有 1 个。
对于全部数据，1≤n≤3×10^9, 1≤m≤3×10^9

这是一题找规律，求通项公式来降低复杂度的题。 找规律的过程见下图：

两个数乘之前要模一下，还要用求和公式，不然会爆…

#include 
#define ll long long 
using namespace std;
const ll Mod=998244353;
ll n,m,sum1,sum2;

int main()
{
	scanf("%lld %lld",&n,&m);
	sum1 = (1+n)*n/2%Mod;
	sum2 = (1+m)*m/2%Mod;
	cout<<sum1*sum2%Mod;
	return 0;	
}

问题 F: 回音 (echo)

时间限制: 1 Sec 内存限制: 128 MB

题目描述
只有回音在生命中，陪伴寒暄着过往
用窒息的孤独感，将身躯花葬
星点的回音汇成声浪
强烈的力量
将心房不断叩响

♪ 她喜欢唱歌。
♪ 她自己写了一首歌。
♪ 她想知道音符出现的次数。
♪ 她又觉得记住每个音符的次数太累。
♪ 她发现其中有一个音符出现频繁到超过总数的一半。
♪ 她只想知道那个音符是什么。

输入
Rainy7：我想要多组数据。
数据：不要。
Rainy7：为什么？
数据：你又不是毒瘤，为啥开多组数据？
Rainy7：好吧。
第一行，输入一个n，表示音符总数。
第二行，输入n个数，表示不同的音符，为了简单区分，每个音符用一个正整数表示。
输出
一行，表示结果。
样例输入
7
1 1 1 4 5 1 4
样例输出
1
提示

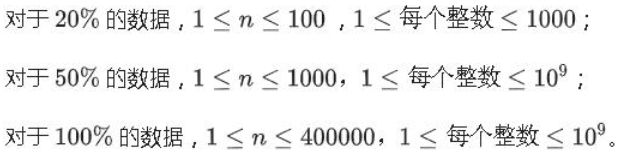
根据题意，当某个数出现的次数超过音符总数的一半时，输出这个数。但数据太大，不能用数组去记录某个音符出现的次数。先进行排序，这样方便之后的判断。int t=1（某个数自身算出现一次），遇到同样的数时，t++，优先判断t的值是否>n/2，符合则输出。

#include 
#define ll long long 
using namespace std;
ll n,a[400010],t=1;

int main()
{
	cin>>n;
	for(int i=1; i<=n; i++)	 scanf("%lld",&a[i]);
	sort(a+1,a+1+n);
		
	for(int i=1; i<=n; i++)
	{
		if(t>n/2) {
			cout<<a[i-1];
			break;
		}

		if(a[i]==a[i+1])  t++;
		else  t=1;    // 没有与之相同的，说明只出现了一次，不符合
	}
 	return 0;
}