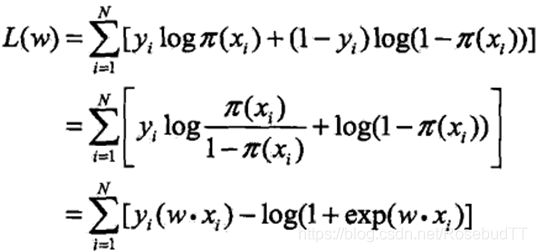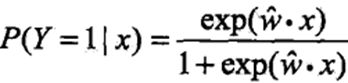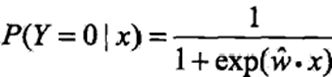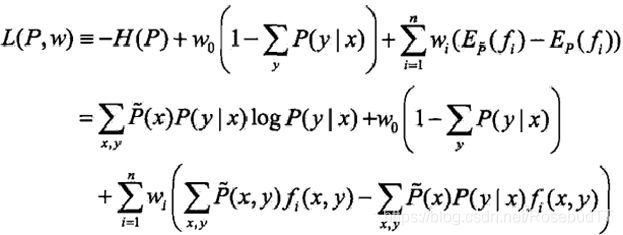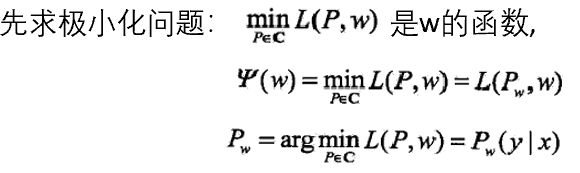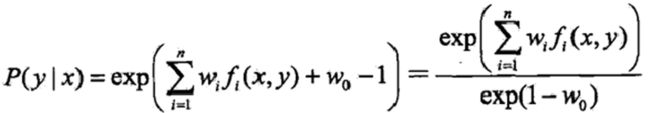机器学习之logistic回归与最大熵模型
根据因变量的不同
•连续:多重线性回归
•二项分布:logistic回归
•poisson分布:poisson回归
•负二项分布:负二项回归
最大熵模型与logistic回归
模型有类似的形式,它们又称为对数线性模型(log linear model).
模型学习就是在给定的训练数据条件下对模型进行极大似然估计或正则化的极大似然估计。
logistic回归
logistic
分类器是由一组权值系数组成的,最关键的问题就是如何获取这组权值,通过极大似然函数估计获得,并且
Y
~
f
(
x
;
w
)
似然函数
是统计模型中参数的函数。
极大似然函数,似然函数取得最大值表示相应的参数能够使得统计模型最为合理
对
L(w)
求极大值,得到
w的估计值。
通常采用梯度下降法及拟牛顿法,学到的模型:
最大熵模型
求
L(
P,w
)
对
P(
y|x)的偏导数,得
# 导入数据,“_orig”代表这里是原始数据,我们还要进一步处理才能使用:
train_set_x_orig, train_set_y, test_set_x_orig, test_set_y, classes = load_dataset()
#由数据集获取一些基本参数,如训练样本数m,图片大小:
m_train = train_set_x_orig.shape[0] #训练集大小209
m_test = test_set_x_orig.shape[0] #测试集大小50
num_px = train_set_x_orig.shape[1] #图片宽度64,大小是64×64
#将图片数据向量化(扁平化):
train_set_x_flatten = train_set_x_orig.reshape(train_set_x_orig.shape[0],-1).T
test_set_x_flatten = test_set_x_orig.reshape(test_set_x_orig.shape[0],-1).T
#对数据进行标准化:
train_set_x = train_set_x_flatten/255.
test_set_x = test_set_x_flatten/255.def sigmoid(z):
a = 1/(1+np.exp(-z))
return a
def initialize_with_zeros(dim):
w = np.zeros((dim,1))
b = 0
return w,b
def propagate(w, b, X, Y):
"""
传参:
w -- 权重, shape: (num_px * num_px * 3, 1)
b -- 偏置项, 一个标量
X -- 数据集,shape: (num_px * num_px * 3, m),m为样本数
Y -- 真实标签,shape: (1,m)
返回值:
cost, dw ,db,后两者放在一个字典grads里
"""
#获取样本数m:
m = X.shape[1]
# 前向传播 :
A = sigmoid(np.dot(w.T,X)+b) #调用前面写的sigmoid函数
cost = -(np.sum(Y*np.log(A)+(1-Y)*np.log(1-A)))/m
# 反向传播:
dZ = A-Y
dw = (np.dot(X,dZ.T))/m
db = (np.sum(dZ))/m
#返回值:
grads = {"dw": dw,
"db": db}
return grads, cost
def optimize(w, b, X, Y, num_iterations, learning_rate, print_cost = False):
#定义一个costs数组,存放每若干次迭代后的cost,从而可以画图看看cost的变化趋势:
costs = []
#进行迭代:
for i in range(num_iterations):
# 用propagate计算出每次迭代后的cost和梯度:
grads, cost = propagate(w,b,X,Y)
dw = grads["dw"]
db = grads["db"]
# 用上面得到的梯度来更新参数:
w = w - learning_rate*dw
b = b - learning_rate*db
# 每100次迭代,保存一个cost看看:
if i % 100 == 0:
costs.append(cost)
# 这个可以不在意,我们可以每100次把cost打印出来看看,从而随时掌握模型的进展:
if print_cost and i % 100 == 0:
print ("Cost after iteration %i: %f" %(i, cost))
#迭代完毕,将最终的各个参数放进字典,并返回:
params = {"w": w,
"b": b}
grads = {"dw": dw,
"db": db}
return params, grads, costsdef predict(w,b,X):
m = X.shape[1]
Y_prediction = np.zeros((1,m))
A = sigmoid(np.dot(w.T,X)+b)
for i in range(m):
if A[0,i]>0.5:
Y_prediction[0,i] = 1
else:
Y_prediction[0,i] = 0
return Y_prediction
def logistic_model(X_train,Y_train,X_test,Y_test,learning_rate=0.1,num_iterations=2000,print_cost=False):
#获特征维度,初始化参数:dim = X_train.shape[0]
W,b = initialize_with_zeros(dim)
#梯度下降,迭代求出模型参数:
params,grads,costs = optimize(W,b,X_train,Y_train,num_iterations,learning_rate,print_cost)
W = params['w']
b = params['b']
#用学得的参数进行预测:
prediction_train = predict(W,b,X_test)
prediction_test = predict(W,b,X_train)
#计算准确率,分别在训练集和测试集上:
accuracy_train = 1 - np.mean(np.abs(prediction_train - Y_train))
accuracy_test = 1 - np.mean(np.abs(prediction_test - Y_test))
print("Accuracy on train set:",accuracy_train )
print("Accuracy on test set:",accuracy_test )
#为了便于分析和检查,我们把得到的所有参数、超参数都存进一个字典返回出来:
d = {"costs": costs,
"Y_prediction_test": prediction_test ,
"Y_prediction_train" : prediction_train ,
"w" : W,
"b" : b,
"learning_rate" : learning_rate,
"num_iterations": num_iterations,
"train_acy":train_acy,
"test_acy":test_acy
}
return d