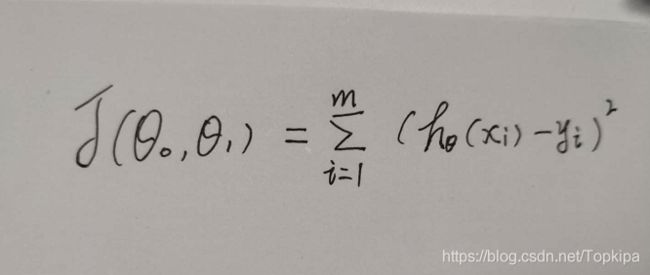笔记整合一：由线性回归到逻辑回归

一、相关概念

1、优化机器学习算法模型参数

1.1 最小二乘法公式：

  观测值就是我们的多组样本，理论值就是我们的假设拟合函数。目标函数也就是在机器学习中常说的损失函数，我们的目标是得到使目标函数最小化时候的拟合函数的模型。

1.2 梯度下降

1、梯度定义：
	微积分中，对多元函数参数求∂偏导数，将求得的各个参数的偏导数以向量形式写出来，即为梯度。
	其本意是一个向量（矢量），表示某一函数在该点处的方向导数沿着该方向取得最大值，
	即函数在该点处沿着该方向（此梯度的方向）变化最快，变化率最大（为该梯度的模）。

2、梯度下降:
	求最小化损失函数，关于损失函数：为了评估模型拟合的好坏，通常用损失函数来度量拟合的程度。
	损失函数极小化，意味着拟合程度最好，对应的模型参数即为最优参数。
	在线性回归中，损失函数通常为样本输出和假设函数的差取平方。
	比如对于m个样本（xi,yi）(i=1,2,...m)（xi,yi）(i=1,2,...m),采用线性回归，损失函数为：

3、梯度下降算法调优：
（1）、步长选择
（2）、算法参数初始值选择
（3）、归一化：由于样本不同特征的取值范围不一样，可能导致迭代很慢，为了减少特征取值的影响，可以对特征数据归一化，也就是对于每个特征x，求出它的期望和标准差，这样特征的新期望为0，新方差为1，迭代次数可以大大加快。

1.3 交叉验证

  交叉验证的基本思想是把在某种意义下将原始数据(dataset)进行分组,一部分做为训练集(train set),另一部分做为验证集(validation set or test set),首先用训练集对分类器进行训练,再利用验证集来测试训练得到的模型(model),以此来做为评价分类器的性能指标。

二.线性回归

  监督学习中，如果预测的变量是离散的，我们称其为分类（如决策树，支持向量机等），如果预测的变量是连续的，我们称其为回归。
  回归分析中，如果只包括一个自变量和一个因变量，且二者的关系可用一条直线近似表示，这种回归分析称为一元线性回归分析。如果回归分析中包括两个或两个以上的自变量，且因变量和自变量之间是线性关系，则称为多元线性回归分析。
  在统计学中，线性回归(Linear Regression)是利用称为线性回归方程的最小平方函数对一个或多个自变量和因变量之间关系进行建模的一种回归分析。

2.1 一般表达式：

Y = aX+b

2.2 解决问题

	所谓回归，是指研究一组随机变量(Yi..和另一组(X...)变量之间关系的统计分析方法回归分析是一种数学模型。
 	当因变量和自变量为线性关系时，它是一种特殊的线性模型.
 	当对大量的观测数据进行处理后，我们可以得到一组比较符合客观事实及事件规律的数学表达式，即根据大量数据的分析找出数据之间的联系所在，从而模拟出相对应的结果，即预测。举个栗子吗，就如同农谚：有雨天边亮，无雨顶上光。均是由多年客观事实形成的经验。

2.3 正则化

  为了防止模型的过拟合，我们在建立线性模型的时候经常需要加入正则化项。一般有L1正则化和L2正则化。
  线性回归的L1正则化通常称为Lasso回归，它和一般线性回归的区别是在损失函数上增加了一个L1正则化的项，L1正则化的项有一个常数系数α来调节损失函数的均方差项和正则化项的权重，
  Lasso回归可以使得一些特征的系数变小，甚至还是一些绝对值较小的系数直接变为0。增强模型的泛化能力。
  线性回归的L2正则化通常称为Ridge回归，它和一般线性回归的区别是在损失函数上增加了一个L2正则化的项，和Lasso回归的区别是Ridge回归的正则化项是L2范数，而Lasso回归的正则化项是L1范数。

2.4注意

  在用线性回归模型拟合数据之前，首先要求数据应符合或近似符合正态分布，否则得到的拟合函数不正确。

三、逻辑回归

3.1 相关概念

3.1.1本质

  逻辑回归本质上是线性回归，只是在特征到结果的映射中加入了一层逻辑函数g(z)，即先把特征线性求和，然后使用函数g(z)作为假设函数来预测。g(z)可以将连续值映射到0 和1。g(z)为sigmoid function.

逻辑回归用来分类0/1 问题，也就是预测结果属于0 或者1 的二值分类问题。
这里假设了二值满足伯努利分布

3.1.2 什么是逻辑回归

  线性回归模型是求输出特征向量Y和输入样本X之间的关系系数θ，一般形式为： Y=aX+b, Y取值范围为[-∞, +∞]，此时，我们的Y是连续的，随意是线性回归问题，可是如果是离散的，或者，我们要对其分类呢？
  于是，我们对于这个Y再做一次函数转换，变为g(Y)。如果我们令g(Y)的值在某个实数区间的时候是类别A，在另一个实数区间的时候是类别B，以此类推，就得到了一个分类模型。如果结果的类别只有两种，那么就是一个二元分类模型了。
  具体做法为把Y的结果带入一个非线性变换的Sigmoid函数中，即可得到[0,1]之间取值范围的数S，S可以把它看成是一个概率值，如果我们设置概率阈值为0.5，那么S大于0.5可以看成是正样本，小于0.5看成是负样本，就可以进行分类了。函数中t无论取什么值，其结果都在[0,-1]的区间内，即非0即1

3.2、离散化原因

  1、逻辑回归属于广义线性模型，表达能力受限；单变量离散化为N个后，每个变量有单独的权重，相当于为模型引入了非线性，能够提升模型表达能力，加大拟合； 离散特征的增加和减少都很容易，易于模型的快速迭代；
  2、速度快！稀疏向量内积乘法运算速度快，计算结果方便存储，容易扩展；
  3、离散化后的特征对异常数据有很强的鲁棒性
  4、特征离散化后，模型会更稳定，并且简化模型，防止过拟合

3.3、TIP

  逻辑回归尤其是二元逻辑回归是非常常见的模型，训练速度很快，虽然使用起来没有支持向量机（SVM）那么占主流，但是解决普通的分类问题是足够了，训练速度也比起SVM要快不少
  那么假设，我要用逻辑回归实现多分类呢？个人意见为：根据每个类别都建立一个二分类器,本类别的样本标签定义为0,其它分类样本标签定义为1,则有多少个类别就构造多少个逻辑回归分类器