【图像特征提取1】方向梯度直方图HOG---从理论到实践------附带积分图像的解析

(一)特征检测算法的综述

          计算机视觉理论中的特征描述是常见的目标分析技术之一，关键点的检测和关键点的提取是目标分析的重要手段和重要步骤之一。局部图像特征描述的核心问题是不变性和可分析性，不变性是基于特征描述对于视角变化的不变性、尺度变化的不变性以及旋转变化的不变性，可分性是基于图像的局部内容的可分性。但是，在实际应用中，不变性和可分性是相互矛盾的。OprnCv中有许多特征检测和提取的算法，例如：SIFT、SURF、ORB、LBP、HOG；Harris角点检测算法、FAST角点检测算法、Harr等。

(二)方向梯度直方图HOG的简介

     Histogram of Oritentd Gradients,缩写为HOG，是目前计算机视觉、模式识别领域很常用的一种描述图像局部纹理的特征。它通过计算和统计图像的局部区域(Cell和Block)的方向梯度直方图来构成特征，按照我的理解就是，先将一整幅图像像划分为大小相等的Cell小区域,比如说，先将图像划分为20pixel*20pixel的小区域，然后，分别计算这些小区域的梯度方向直方图；然后，再由一定数量的小区域组成稍微大一点的区域Block，比如说由2*2个Cell小区域组成1个Block区域，然后，再由Block区域的方向梯度直方图特征向量组成整幅图像的方向梯度直方图HOG的特征向量；现在，这个特征向量就可以唯一的描述这幅图像，就像一个人的身份证编号(特征向量)一样，可以代表描述一个人。求出一幅图像的HOG特征向量之后，这个特征向量就可以结合SVM，实现目标检测，以图搜图；HOG+SVM刚开始的时候，是被广泛用于行人检测的，当然也可以用于其它方向的检测或者以图搜图等领域。

（三）方向梯度直方图HOG算法的大致步骤如下所示:

      1）归一化处理

       归一化处理操作的目的是：为了提高图像特征描述符对光照以及环境变化的鲁棒性，降低图像局部的阴影、局部曝光过多及纹理失真，尽可能的抑制图像的干扰噪声。归一化处理操作是先将图像转化为灰度图像，再利用Gamma校正实现。

        2）分割图像

       因为方向梯度直方图HOG是一个描述图像局部纹理信息的局部特征描述符，因此，如果直接对一大幅图像及逆行特征提取的话，将会得不到好的效果。因此，我们需要先将图像划分为较小的方格单元，比如我们在程序中先将图像划分为20*20大小的放格单元Cell，然后2*2个Cell组成一个Block，最后，所有的Block组成图像。

     HOG图像的划分一般有两种策略，重叠和不重叠，即overlap和non-overlap两种。这两种划分策略应该很好理解。就不多说了，直接看一下non-overlap的划分策略示意图，如下图所示：

对于图像I(x,y),计算图像在水平方向和垂直方向上的梯度，这一步我们可以利用OpenCv中的一阶微分算子Sobel计算得到。

         

      3)计算每个Cell的方向梯度直方图

         将图像划分为小的Cell之后，接下来就是计算每一个Cell的方向梯度直方图，我们可以利用OpenCv中的一阶微分算子函数Sobel对每一个小区域求解X方向和Y方向上的梯度图像。然后，再根据下面的公式(1)和公式(2)计算每一个小区域中每一个像素点的梯度方向和梯度幅值。

      通过上面公式计算出来的梯度方向的角度是一个范围在0~360度的弧度值，为了计算简单，我们将梯度向的范围约束为0~180度，并且分割为9个方向，每个方向20度，再将约束后的角度除以20，则现在的梯度方向角度值就变为范围在[0,9)，我们现在将每个小Cell里面的梯度幅值按照这9个方向进行统计，计算完之后，将会产生一个横坐标X为梯度方向，纵坐标Y为梯度幅值的方向梯度直方图。

 

      4）特征向量归一化

     为了克服光照不均匀的变化以及前景和背景测对比差异，需要对每个小区域计算出来的特征向量进行归一化处理。在程序中，我们直接使用OpenCv中的normalize函数中的CV_L2范数进行归一化处理。

    5）HOG特征向量的生成

      首相，我们将图像中的小Cell的HOG特征向量组成比较大的Block的HOG特征向量，具体组合方式就是利用2*2个Cell组成一个Block。然互再将所有的Block的HOG特征向量组成全图像的HOG特征向量。特征向量的具体组合方式是将小的特征向量按照首尾相接的方式组成一个维数比较大的特征向量。比如，一幅图像被分为m*n个Block，每一个Block的特征向量的维数为9维(每一个梯度方向就是一维)。那么，这个图像最终的特征向量维数就是m*n*9。

（四）积分图像

      在计算HOG方向梯度直方图特征时，如果按照上面说的直接对每一个小块进行梯度、梯度幅值、角度的计算，然后在进行统计，这样做的话，HOG的计算复杂度将会十分大，因此，我们可以将积分图的概念引入HOG的计算，以便加速HOG的计算性能。

      积分图就是:对于一幅灰度图像而言，如果每一像素点的灰度值等于该像素点左上矩形区域所有像素点的灰度值之和，那么这幅图像就是积分图像。

      1）为什么要用积分图像

      图像直方图的计算方法为：遍历图像中的全部像素并累加计算每个灰度强度值出现的次数。但是，有时候需要计算图像中多个特定区域的直方图的，如果按照上面的计算方法进行计算的话，这个求解过程将会变得十分的耗时。在这种情况下使用积分图像将会极大的提高统计图像子区域像素的效率。

       2）积分图像的概念

      积分图就是:对于一幅灰度图像而言，如果每一像素点的灰度值等于该像素点左上矩形区域所有像素点的灰度值之和，那么这幅图像就是积分图像。

       3）OpenCv中计算积分图像的C++接口

//! computes the integral image
CV_EXPORTS_W void integral( InputArray src, OutputArray sum, int sdepth=-1 );
//! computes the integral image and integral for the squared image
CV_EXPORTS_AS(integral2) void integral( InputArray src, OutputArray sum,OutputArray sqsum, int sdepth=-1 );
//! computes the integral image, integral for the squared image and the tilted integral image
CV_EXPORTS_AS(integral3) void integral( InputArray src, OutputArray sum,OutputArray sqsum, int sdepth=-1 );

   

          按照积分图的概念，P0点的像素强度积分值就是蓝色方框中的所有像素点的强度累加和，P3点的像素强度累加和就是黄色区域所有像素强度的累加和。从上述图像可知，想要从原始图想获得积分图像，只需要对原始图像进行一次扫描。为了防止累加和过大产生溢出现象，积分图像通常使用CV_32S或者CV_32F类型的矩阵或者图像存储。对于多通道图像，每个通道将独立的计算各自的积分图像。

     这样的话，如果我们需要计算图像中任意的某一特定区域的像素强度的话，我们只需要进行加减运算，而不需要变量图像。例如现在我们需要计算像素点P0,P1,P2,P3围城的矩形区域的像素强度累加，只需要按照下面的这个公式计算就可以了:

                         矩形区域的像素强度值 = P3 -P1 - P2 + P0

      另外，由于网上关于积分图的概念和定义不是那么的一致，现在我们给出OpenCv官方文档的参考资料，关于积分图的计算介绍如下所示:

                                      

（五）基于OpenCv和C++方向梯度直方图HOG特征向量描述符的实现

           具体的程序如下所示，至于在HOG中引入积分图思想之后，HOG算法的计算流程，程序中已经做了详细的说明。

/********************************************************************************************************
文件说明:
        HOG特征描述符的实现
算法思路:
        1)将图片加载入内存，并且利用cvtColor将图像转换为grayImg
		2)利用一阶微分算子Sobel函数，分别计算出grayImg图像X方向和Y方向上的一阶微分/梯度图像
		3)根据得到的两幅梯度图像(X方向上的梯度图像和Y方向上的梯度图像)，然后利用cartToPolar函数，计算出这
		      两幅梯度图像所对应的角度矩阵图像angleMat和梯度幅值矩阵图像magnMat
		4)将角度矩阵图像angleMat里面的像素强度值归一化为强度范围在[0，9）这9个范围，每一个范围就代表HOG中
		      的一个bins
		5)以角度为为索引，将梯度幅值图像矩阵magnMat按照九个方向的梯度角度拆分为9幅梯度幅值图像矩阵
		6)根据这9个角度，每个角度所对应的梯度幅值图像矩阵，并且利用OpenCv中的积分函数integral分别计算出这9
		      幅图像所对应的积分图像
		==============至此，我们9个梯度方向上，分别对应的的9幅梯度幅值积分图已经计算完毕==================
		7)计算整幅图像的梯度方向直方图HOG:要计算整幅图像的，需要先计算每个Block的HOG；要计算每个Block的HOG
		      要先计算每个Cell的HOG
		8)计算单个Cell的HOG:由于9个梯度方向上的9张梯度幅值积分图像已经计算出来，所以这一步的计算很简单，只需
		      要记性加减计算，具体的函数为cacHOGinCell
		9)计算单个Block的HOG:将计算出来的4个Cell的HOG组成一个Block的HOG
		10)计算整幅图像的HOG:将计算出来的所有的Block的HOG梯度方向直方图的特征向量首尾相接组成一个维度很大的
		      整幅图像的梯度方向直方图的HOG特征向量，这个特征向量就是整幅图像的梯度方向直方图特征，这个特征
			  向量也可以被用于SVM的分类
算法难点:
        1)积分图像的概念:网上有关积分图像的Blog一大推，但是很多讲的都不准确，最好的办法是看OpenCv的官方文档
		      关乎积分函数的讲解，可以结合网上的资料看
		2)笛卡尔空间坐标和极坐标的转换(关键是理解一些它们之间相互转换的前提条件)
		3)L1范数和L2范数:在使用归一化normalize函数时，考虑一些CV_L2到底是向量的L2范数还是矩阵的L2范数，自己
		      可以推到一下公式
		4)关于HOG的论文，没有使用到积分图的概念，其实在HOG中使用积分图像加速了HOG的计算速度，如果使用先计算
		      梯度，在计算各个区域的梯度方向和梯度幅值的话，这样计算了太大，会导致HOG的性能有所下降
	    5)还有，这里的每个Cell的大小是20p*20p,每个Block的大小为4个Cell；当然如果用于行人检测的话，也可以使用
		      其他的3*3或者5*5组合
开发环境:
        Win7 + OpenCv2.4.8 + VS2012
时间地点:
        陕西师范大学 2017.3.14
作    者:
        九 月
*********************************************************************************************************/
#include 
#include 
#include 
#include 

using namespace cv;
using namespace std;

#define NBINS 9
#define THETA 180 / NBINS
#define CELLSIZE 20
#define BLOCKSIZE 2
#define R (CELLSIZE * (BLOCKSIZE) * 0.5)
/********************************************************************************************************
函数功能:
        计算积分图像
参数说明:
        Mat& srcMat-----------------------存储每个cellHOG特征的行特征向量
		2)cv::Rect roi--------------------单个cell的矩形位置
		3)std::vector& integrals-----存储的9幅积分图像，每一幅积分图像代表一个角度范围或者一个bins
*********************************************************************************************************/
// 计算积分图
std::vector CalculateIntegralHOG(Mat& srcMat)
{
	//【1】计算一阶微分的梯度图像
	cv::Mat   sobelMatX;
	cv::Mat   sobelMatY;

	cv::Sobel(srcMat, sobelMatX, CV_32F, 1, 0);
	cv::Sobel(srcMat, sobelMatY, CV_32F, 0, 1);

	std::vector bins(NBINS);
	for (int i = 0; i < NBINS; i++)
	{
		bins[i] = Mat::zeros(srcMat.size(), CV_32F);
	}
	cv::Mat   magnMat;
	cv::Mat   angleMat;
	//【2】坐标转换,根据每一个点X方向和Y方向上的梯度，实现笛卡尔坐标和极坐标的转换
	cartToPolar(sobelMatX, sobelMatY, magnMat, angleMat, true);
	//【3】下面这这两行代码起始是做安全处理的，因为在将笛卡尔坐标转换为极坐标之后，角度的范围在[0,360]
	//     下面这两行代码让所有的角度收缩在[0,180]这个返回
	add(angleMat, Scalar(180), angleMat, angleMat<0);                //如果angleMat<0，则加180
	add(angleMat, Scalar(-180), angleMat, angleMat >= 180);          //如果angleMat>=180，则减180
	//【4】下面这行代码将角度矩阵转换为一个灰度值范围在[0,9]之间的图像
	angleMat /= THETA;
	//【5】下面这个循环，其实是将图像的梯度幅值矩阵按九个不同方向的梯度角度，将每个角度范围内相应点的梯度幅值
	//     存储在相应的矩阵图像之上，其实就是将梯度幅值矩阵图像按照不同的梯度幅值角度分为9幅梯度幅值的图像
	for (int y = 0; y < srcMat.rows; y++)
	{
		for (int x = 0; x < srcMat.cols; x++)
		{
			int ind = angleMat.at(y, x);
			bins[ind].at(y, x) += magnMat.at(y, x);  
		}
	}
	//【6】根据上面生成的9张不同角度的梯度幅值矩阵生成9张不同的梯度幅值的积分图像，至此以后，
	//     积分图像的每一点就代表，这一点左上角，所有梯度幅值之和；生成的9幅积分图也就是9个
	//     bins，不同bins上的HOG强度
	std::vector integrals(NBINS);
	for (int i = 0; i < NBINS; i++)
	{
		integral(bins[i], integrals[i]);
	}
	return integrals;
}
/********************************************************************************************************
函数功能:
        计算单个cell HOG特征
参数说明:
        1)cv::Mat& HOGCellMat-------------存储每个cellHOG特征的行特征向量
		2)cv::Rect roi--------------------单个cell的矩形位置
		3)std::vector& integrals-----存储的9幅积分图像，每一幅积分图像代表一个角度范围或者一个bins
*********************************************************************************************************/
void cacHOGinCell(cv::Mat& HOGCellMat,cv::Rect roi,std::vector& integrals)
{
	//【1】通过9幅积分图像快速实现HOG的计算，HOG这个直方图有9个bins，每个bins就对应一张积分图像
	int x0 = roi.x;                              //确定单个矩形cell的左上角点坐标
	int y0 = roi.y;
	int x1 = x0 + roi.width;
	int y1 = y0 + roi.height;                    //确定单个矩形cell的右下角点坐标

	for(int i = 0;i (y0,x0);
		float b = integral.at(y1,x1);
		float c = integral.at(y0,x1);
		float d = integral.at(y1,x0);

		HOGCellMat.at(0,i) = b - c - d +a;//每循环一次，计算一个梯度方向上的HOG特征，其实就是
		                                          //每循环一次，就计算梯度方向直方图上的一个bins
	}
}
/********************************************************************************************************
函数功能:
        获取当前窗口的HOG直方图----此块其实就是在计算单个Block的HOG梯度方向直方图
参数说明:
        1)cv::Point pt--------------------单个Block的中心点坐标
		2)std::vector& integrals-----存储的9幅积分图像，每一幅积分图像代表一个角度范围或者一个bins
*********************************************************************************************************/
cv::Mat getHog(cv::Point pt,std::vector& integrals)
{
	if(pt.x - R<0||pt.y-R<0||pt.x+R>=integrals[0].cols||pt.y+R>=integrals[0].rows)
	{
		return cv::Mat();
	}
	//【1】BLOCK的HOG直方图---具体的来说，BLOCKSIZE*BLOCKSIZE即4个cell的HOG特征直方图特征向量
	//     组成一个BLOCK的HOG特征直方图的特征向量
	cv::Mat    hist(cv::Size(NBINS*BLOCKSIZE*BLOCKSIZE,1),CV_32F);
	cv::Point  t1(0,pt.y-R);
	int c = 0;
	//【2】遍历块:通过下面这两个循环，就遍历了4个cell，并且将4个cell的HOG特征向量组成了一个
	//     维数比较大的BLOCK的HOG特征向量
	for(int i=0;i cacHOGFeature(cv::Mat srcImage)
{
	cv::Mat          grayImage;
	std::vector HOGMatVector;
	cv::cvtColor(srcImage, grayImage, CV_RGB2GRAY);
	grayImage.convertTo(grayImage, CV_8UC1);
	//【1】9个不同梯度方向上的9张梯度幅值的积分图像的生成
	std::vector integrals = CalculateIntegralHOG(grayImage);
	Mat image = grayImage.clone();
	image *= 0.5;
	//【2】变量全图像，计算最终的梯度方向直方图HOG
	cv::Mat HOGBlockMat(Size(NBINS, 1), CV_32F);
	for (int y = CELLSIZE / 2; y < grayImage.rows; y += CELLSIZE)
	{
		for (int x = CELLSIZE / 2; x < grayImage.cols; x += CELLSIZE)
		{
			//【3】获取当前窗口HOG，其实当前的窗口就是一个Block，每个Block由四个cell组成，每个Cell为20*20
			//     此块，计算的就是单个Block的梯度方向直方图HOG
			cv::Mat hist = getHog(Point(x, y), integrals);
			if (hist.empty())continue;
			HOGBlockMat = Scalar(0);
			for (int i = 0; i < NBINS; i++)
			{
				for (int j = 0; j < BLOCKSIZE; j++)
				{
					HOGBlockMat.at(0, i) += hist.at(0, i + j*NBINS);
				}
			}
			//【4】L2范数归一化:对其得到的每个Block的的矩阵进行L2范数归一化，使其转变为一个Block的HOG特征向量
			normalize(HOGBlockMat, HOGBlockMat, 1, 0, CV_L2);
			//【5】最后，每得到一个Block的HOG特征向量就存入HOGMatVector，这个HOGMatVector其实就是整个图像的HOG特征向量，
			//     当然，现在这个HOGMatVector还是个二维数组的形式，如果想要利用SVM对其进行分类的话，还需要将其拉伸为一
			//     维特征向量
			HOGMatVector.push_back(HOGBlockMat);
			Point center(x, y);
			//【6】绘制HOG特征图
			for (int i = 0; i < NBINS; i++)
			{
				double theta = (i * THETA ) * CV_PI / 180.0;
				Point rd(CELLSIZE*0.5*cos(theta), CELLSIZE*0.5*sin(theta));
				Point rp = center - rd;
				Point lp = center + rd;
				line(image, rp, lp, Scalar(255 * HOGBlockMat.at(0, i), 255, 255));
			}
		}
	}
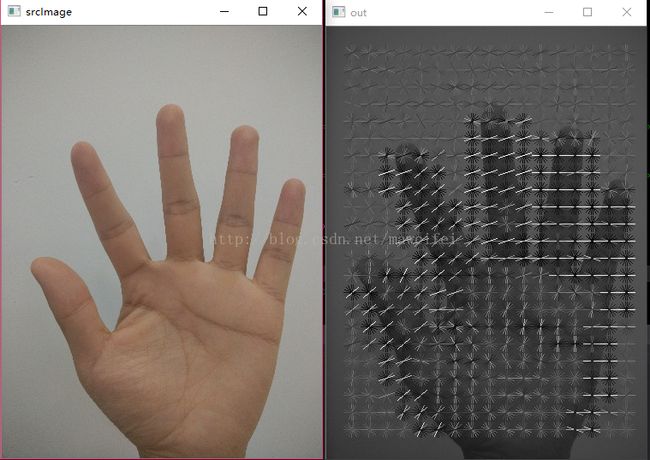
	imshow("out", image);
	return HOGMatVector;
}
/********************************************************************************************************
模块功能:
        控制台应用程序的入口:Main函数
*********************************************************************************************************/
int main()
{
	cv::Mat srcImage = cv::imread(".\\images\\hand1.jpg");
	if (srcImage.empty())
		return -1;
	cv::imshow("srcImage ", srcImage);
	std::vector HOGFeatureMat = cacHOGFeature(srcImage);
	cv::waitKey(0);
	return 0;
}