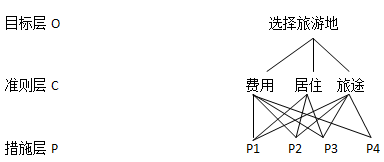
层次分析法 方案层判断矩阵阶数不同解决方案
准则层的每个指标均与措施层的每个指标都具有联系和比重。在措施层的维度较多时,可能出现的情况是

准则层判断矩阵
| 费用 | 饮食 | 旅途 | |
|---|---|---|---|
| 费用 | 1 | 3 | 5 |
| 饮食 | 1/3 | 1 | 1 |
| 旅途 | 1/5 | 1 | 1 |
方案层判断矩阵分别为
| P1 | P2 | P3 | |
|---|---|---|---|
| P1 | 1 | 1/3 | 1/3 |
| P2 | 3 | 1 | 1 |
| P3 | 3 | 1 | 1 |
| P4 | P5 | |
|---|---|---|
| P4 | 1 | 1/5 |
| P5 | 5 | 1 |
| P6 | P7 | P8 | |
|---|---|---|---|
| P6 | 1 | 3 | 1 |
| P7 | 1/3 | 1 | 1 |
| P8 | 1 | 1 | 1 |
上面的情况是最极端的情况(措施层的指标仅与决策层的一个指标相关),而本文针对任何形式的方案层判断矩阵阶数不同。
经典的层次分析法的代码假定方案层判断矩阵阶数相同,所以需要进行一定的修正。在了解代码的运算方式后发现,各个矩阵的计算是独立的,所以对其中一个矩阵进行加阶数(多余的位置全部加1),这样的处理并不影响其他矩阵的运算结果。
使用的文档temp.txt的数据是
1 3 5
1/3 1 1
1/5 1 1
1 1/3 1/3
3 1 1
3 1 1
1 5 1
1/5 1 1
1 1 1
1 3 1
1/3 1 1
1 1 1
MATLAB代码块
clc,clear
fid=fopen('temp.txt','r');
n1=3;n2=3;
a=[];
for i=1:n1
tmp=str2num(fgetl(fid));
a=[a;tmp]; %读准则层判断矩阵
end
for i=1:n1
str1=char(['b',int2str(i),'=[];']);
str2=char(['b',int2str(i),'=[b',int2str(i),';tmp];']);
eval(str1);
for j=1:n2
tmp=str2num(fgetl(fid));
eval(str2); %读方案层的判断矩阵
end
end
ri=[0,0,0.58,0.90,1.12,1.24,1.32,1.41,1.45]; %一致性指标
[x,y]=eig(a);
lamda=max(diag(y));
num=find(diag(y)==lamda);
w0=x(:,num)/sum(x(:,num));
cr0=(lamda-n1)/(n1-1)/ri(n1)
for i=1:n1
[x,y]=eig(eval(char(['b',int2str(i)])));
lamda=max(diag(y));
num=find(diag(y)==lamda);
w1(:,i)=x(:,num)/sum(x(:,num));
cr1(i)=(lamda-n2)/(n2-1)/ri(n2);
end
cr1, ts=w1*w0, cr=cr1*w0
对于之前略过的二阶矩阵,可以最后单独求解。
使用的文档temp_2.txt的数据是
1 5
1/5 1
MATLAB代码
clc,clear
fid=fopen('temp_2.txt','r');
n1=2;n2=3;
a=[];
for i=1:n1
tmp=str2num(fgetl(fid));
a=[a;tmp]; %读准则层判断矩阵
end
ri=[0,0,0.58,0.90,1.12,1.24,1.32,1.41,1.45]; %一致性指标
[x,y]=eig(a);
lamda=max(diag(y));
num=find(diag(y)==lamda);
w0=x(:,num)/sum(x(:,num));
cr0=(lamda-n1)/(n1-1)/ri(n1)
cr0
简而言之,删改后的代码块可以仅计算一个矩阵对应的CR值、权重。