求无向连通图的最小生成树(c语言版)
完整源码地址:[email protected]:hglspace/MinCostSpTree.git
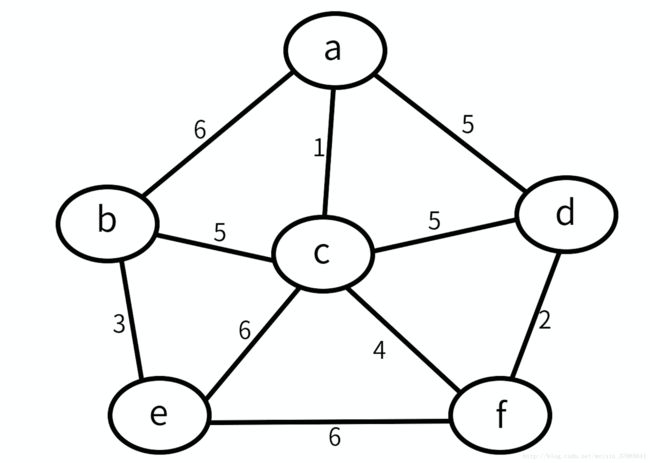
图例:
1 普里姆算法
/*
普里姆算法:假设N={v,{E}}是连通图,TE是N上的最小生成树中边的集合,算法从U={u0}(u0属于V),TE={}开始,重复执行下述操作:
在所有u属于U,v属于V-U的边
*/
void MiniSpanTree_PRIM(structGraph g,structvert u){
struct tmp closedge[MAX_VEX_NUM];
int index=u.index,i,j;
int minimum(structtmp closedge[]);
for(j=0;j
if(j!=index){
closedge[j].lowcost=g.arcs[index][j].cost;
closedge[j].vex=u;
}
}
closedge[index].lowcost=0;//自己到自己的最小权值是0
for(i=1;i
index=minimum(closedge);
if(index<0){
printf("此图不是连通图\n");
exit(0);
}
printf("下一个顶点是:%c,权值是:%d\n",g.vexs[index].data,closedge[index].lowcost);
closedge[index].lowcost=0;
for(j=0;j
if(g.arcs[index][j].cost
closedge[j].lowcost=g.arcs[index][j].cost;
closedge[j].vex=g.vexs[index];
}
}
}
}
int minimum(structtmp closedge[]){//求closedge数组中最小权值的边,返回V-U中的顶点位置
int i,tlow=999,index=-1;
for(i=0;i<MAX_VEX_NUM;i++){
if(tlow>closedge[i].lowcost && closedge[i].lowcost>0){
tlow=closedge[i].lowcost;
index=i;
}
}
return index;
}
2 克鲁斯卡尔算法
/*
克鲁斯卡尔:假设连通图N={v,{E}},则令最小生成树的初始状态为只有n个顶点而无边的非连通图T={v,{}},图中每个顶点自称一个连通分量。在E中选择代价最小的边,
若该边依附的顶点落在T中不同的连通分量上,则将此边加入到T中,否则舍去此边而选择下一条代价最小的边。以此类推,直至T中所有的顶点都在同一连通分量上为止。
*/
void MiniSpanTree_KRUSKAL(structGraph g){//把当前图用邻接多重链表存储?
//把邻接矩阵结构存储的图转化为邻接多重链表结构,原因是:方便下面查找两个顶点是否在同一个连通图中,并且会多次遍历查找
int i,j,n=1;
struct arc getMinArc(structGraph * g,structAmGraph amg);
struct arc a;
struct AmGraph amg={};
for(i=0;i
struct VexBox v;
v.data=g.vexs[i].data;
v.firstedge=NULL;
v.mark=False;
amg.vb[i]=v;
}//初始化后,所有的顶点都是孤立的,并没有任何边
//按照定义开始选择边
while(n
struct Ebox * e=(structEbox *)malloc(sizeof(structEbox));
a=getMinArc(&g,amg);//把找到的边存放到多重链表结构的图中
e->cost=a.cost;
e->ivex=a.head;
e->jvex=a.tail;
e->ilink=NULL;
e->jlink=NULL;
e->mark=False;
//把a添加到amg中
if(amg.vb[a.head].firstedge==NULL){
amg.vb[a.head].firstedge=e;
}else{
e->ilink=amg.vb[a.head].firstedge;
amg.vb[a.head].firstedge=e;
}
if(amg.vb[a.tail].firstedge==NULL){
amg.vb[a.tail].firstedge=e;
}else{
e->jlink=amg.vb[a.tail].firstedge;
amg.vb[a.tail].firstedge=e;
}
n++;
}
for(i=0;i
for(j=i+1;j
if(g.arcs[i][j].cost==0){//找到合适的边,会把其权值置为0,这里根据这个特点输出
printf("头顶点:%c,尾顶点:%c,权值是:%d\n",g.vexs[i].data,g.vexs[j].data,g.arcs[i][j].tmpcost);
}
}
}
}
/*
获取合适的边
*/
struct arc getMinArc(structGraph * g,structAmGraph amg){
int i,j,head,tail,tmp=999;
struct arc a;
Bool judgeLt(int head,int tail,structAmGraph g);
for(i=0;i
for(j=i+1;j
if(g->arcs[i][j].cost>0 && tmp>g->arcs[i][j].cost){
head=g->arcs[i][j].head;
tail=g->arcs[i][j].tail;
Vexflag=False;//在每次调用判断两个顶点是否在同一连通分量的方法之前,一定要把全局变量Vexflag置为False,排除上一次查找的结果的干扰
if(judgeLt(head,tail,amg)){
continue;
}
tmp=g->arcs[i][j].cost;
a=g->arcs[i][j];
}
}
}
g->arcs[a.head][a.tail].tmpcost=g->arcs[a.tail][a.head].tmpcost=a.cost;
g->arcs[a.head][a.tail].cost=g->arcs[a.tail][a.head].cost=0;
return a;
}
/*
判断该边依附的两个顶点是否在同一连通分量上
*/
Bool judgeLt(int head,int tail,structAmGraph g){
//遍历该图,判断这两个顶点是否在一个连通分量上
Bool DFSTree(structAmGraph g,int v1,int v2,structEbox * ebs[]);
struct Ebox * ebs[MAX_EDG_NUM]={};
int i;
Bool flag=DFSTree(g,head,tail,ebs);
//一定要把amg的边的mark再置为False,下次再调用,mark还是默认值,每次查找,多重链表图都应该是原始的,标志变量一定要改回原来的状态
for(i=0;ebs[i]!=NULL;i++){
ebs[i]->mark=False;
}
return flag;
}
Bool DFSTree(structAmGraph g,int v1,int v2,structEbox * ebs[]){
int i;
int getAdjVex(structAmGraph * g,int v,structEbox * ebs[]);
for(i=getAdjVex(&g,v1,ebs);i>0;i=getAdjVex(&g,v1,ebs)){
if(!g.vb[i].mark){//其实这个判断不加也行,加这个判断主要是排除两个顶点之间有回路的情况,而现在的情况是这两个顶点之间不会有回路的
g.vb[i].mark=True;
if(i==v2){
Vexflag=True;
}
}
DFSTree(g, i, v2,ebs);
}
returnVexflag;
}
/*
获取该顶点的邻接顶点
*/
int getAdjVex(structAmGraph * g,int v,structEbox * ebs[]){
int i;
for(i=0;ebs[i]!=NULL;i++);
struct Ebox * e=g->vb[v].firstedge;
if(e==NULL){
return -1;
}
for(;e!=NULL&&e->mark==True;){
if(e->ivex==v){
e=e->ilink;
}else{
e=e->jlink;
}
}
if(e==NULL){
return -1;
}else{
ebs[i]=e;//把遍历过的边,放在esb数组中,调用结束后,把该边的状态置为原始值
e->mark=True;
if(e->ivex==v){
return e->jvex;
}else{
return e->ivex;
}
}
}