C语言浮点数存储方式

C语言浮点数存储方式

对于浮点类型的数据采用单精度类型(float)和双精度类型(double)来存储，float数据占用 32bit,double数据占用 64bit.其实不论是float类型还是double类型，在计算机内存中的存储方式都是遵从IEEE的规范的，float 遵从的是IEEE R32.24 ,而double 遵从的是R64.53。

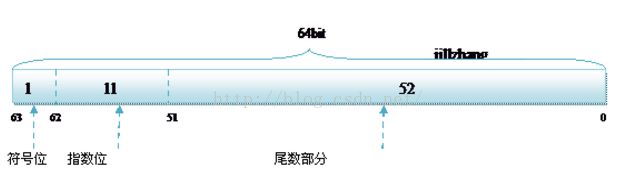
无论是单精度还是双精度，在内存存储中都分为3个部分：

1. 符号位(Sign)：0代表正，1代表为负；

2. 指数位(Exponent)：用于存储科学计数法中的指数数据，是无符号数。同时因为指数可正可负，所以采用移位存储；

3. 尾数部分(Mantissa)：尾数部分

其中float的存储方式如下图所示：

而双精度的存储方式为:

R32.24和R64.53的存储方式都是用科学计数法来存储数据的

用二进制的科学计数法第一位都是1嘛，干嘛还要表示呀？可以将小数点前面的1省略，所以23bit的尾数部分，可以表示的精度却变成了 24bit，道理就是在这里。

那24bit能精确到小数点后几位呢，我们知道9的二进制表示为1001，所以4bit能精确十进制中的1位小数点，24bit就能使float能精确到小数点后6位，而对于指数部分，因为指数可正可负，8位的指数位能表示的指数范围就应该为:-127-128了， 所以指数部分的存储采用移位存储，存储的数据为原数据+127。

下面就看看8.25和120.5在内存中真正的存储方式：

首先看下8.25，用二进制的科学计数法表示为
:1.00001*2^3 按照上面的存储方式，符号位为0，表示为正；指数位为3+127=130，位数部分为 1.00001，故8.25的存储方式如下： 0xbffff380（物理地址）: 01000001000001000000000000000000

分解如下：0–10000010–00001000000000000000000

符号位为0，指数部分为10000010，位数部分为 00001000000000000000000

同理，120.5在内存中的存储格式如下： 0xbffff384（物理地址）: 01000010111100010000000000000000

分解如下：0–10000101–11100010000000000000000

那么如果给出内存中一段数据，并且告诉你是单精度存储的话，你如何知道该数据的十进制数值 呢？其实就是对上面的反推过程，比如给出如下内存数据： 01000001001000100000000000000000

第一步：符号位为0，表示是正数； 第二步：指数位为10000010，换算成十进制为130，所以指数为130-127=3； 第三步：尾数位为01000100000000000000000，换算成十进制为 (1+1/4+1/64)； 所以相应的十进制数值为：2^3*(1+1/4+1/64)=8+2+1/8=10.125

Reference
https://blog.csdn.net/shenziheng1/article/details/79471340

现在我们知道, 对于32位flaot而言: 尾数(含隐藏的整数部分)的可取值为: [1 ,2), 指数位可取值[-126, 127]且浮点数可正可负, 所以32位float的取值范围是:[-2 * 2^127, -1 * 2^-126] ∪ [1 * 2^-126, 2 * 2^{127]约等于:[-3.4*10}38, -1.1810^-38] ∪ [1.1810^-38, 3.4 * 10^38]浮点数的取值范围即这样计算出来的.下面是 32位float浮点数的取值范围示意图, 可以参照此图更好的理解一下

x轴代表以2为底的n次幂(即内存中的指数部分), y轴代表尾数(含隐藏的整数部分1.)坐标系中任意一点(x, y)就代表一个浮点数,这一点到x轴, y轴所围成的矩形的面积即这个浮点数的值 (即浮点数的值 = 尾数(含隐藏的整数部分) * 以2为底的n次幂, 例子可以参见下面的一张图)

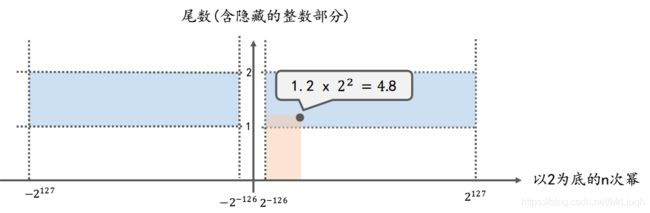
蓝色部分表示浮点数取值范围, 即用于表示浮点数的坐标点只能出现在坐标轴中的蓝色区域.

坐标点表示一个浮点数

橙色部分的面积表示该浮点数的值.

这就是32位浮点数取值范围的计算方法