群体智能优化算法之 分组教学优化算法(Group teaching optimization algorithm,GTOA)

获取更多资讯，赶快关注公众号(名称：智能制造与智能调度，公众号：deeprlscheduler)吧！

第三十二章 分组教学优化算法（Group teaching optimization algorithm,GTOA）

很多传统的智能优化算法往往需要很多额外的控制参数，而每个参数设置都需要一定的先验知识，或不断尝试，一旦这些参数设置的不合适，就会严重影响算法的优化性能。为了解决这样的问题，天津大学的Yiying Zhang于2020年提出了一种新的全局优化算法——分组教学优化算法(Group teaching optimization algorithm,GTOA)。

该算法受到分组教学机制的启发。分组教学是一种常见的教学模式，可以简述如下:学生首先按照规定的规则被分成若干组，然后结合每个小组的特点，教师会运用具体的教学方法来提高小组的知识。

基本思想

在中国历史上，孔子最早提出了"因材施教"的教育理念，就是说教师应该根据不同学生的特点制定适合他们的教学方法，所以GTOA的思想在于通过模仿分组教学来提升整个班级的知识水平。考虑到学生之间的各种差异，分组教学在实践中实施起来比较复杂。为了使分组教学适应于作为一种优化技术，我们首先假设种群、决策变量和适应度值分别与学生、提供给学生的课程和学生的知识类似。在此基础上，定义了4条规则，构建了一个简单且不失一般性的分组教学模型：

1. 学生之间的唯一区别在于接受知识的能力，学生接受知识的能力差异越大，教师在制定教学计划时面临的挑战就越大。
2. 一个好的教师往往更关注接受知识能力较差的学生，而不是接受知识能力较强的学生。
3. 在课余时间，学生可以通过自学和与其他学生的交流来获得自己的知识。
4. 良好的教师分配机制对提高学生的知识水平非常有帮助。

GTOA框架

GTOA的分组教学模型中存在4个阶段，包括教师分配阶段、能力分组阶段、教师阶段和学生阶段，如下图所示。

能力分组阶段

不失一般性，可以假设整个班级的知识服从正太分布：

$$f(x)=\frac{1}{\sqrt{2\pi }\delta }{e}^{\frac{-(x-u{)}^2}{2{\delta }^2}}\text{\hspace{1em}(1)}$$

其中$u$为整个班级的平均知识水平，$\delta$为标准差。一位优秀的教师不仅要考虑如何提高平均知识$u$，而且要考虑如何减少标准差$\delta$。为了为了实现这一目标，教师应该针对其学生制定合适的教学计划。

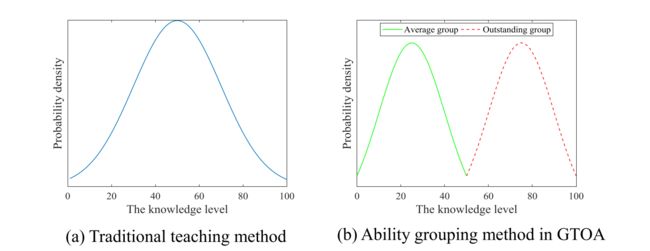
上图为两种不同教学方法的分布模型，图(a)为传统教学方法的知识分布，可以看出该分布相对分散。为了更好地表现分组教学的特点，可以将所有学生根据接受知识的水平分成两组，这两个组在GTOA中同等重要，因而这两组具有相同的学生数量。接受能力强的学生称为出色学生或优秀学生，而接受能力差一点的则称为一般学生或平庸学生。图(b)展示了基于能力分组的知识分布，可以看出出色组和一般组的标准差比(a)中的小很多。考虑到第一条规则，由于标准差变小，教师在制定教学计划时更容易采用能力分组法，而不是传统的教学方法。值得注意的是，在图(b)中，出色组和一般组的标准差可能会随着教学活动的进行而增大。为了解决这个问题，能力分组在GTOA中是一个动态的过程，需要每当在一个学习周期结束之后再进行一次分组。

教师阶段

教师阶段意味着学生从教师那学习知识，这对应于第二条规则。在GTOA中，教师为一般组和出色组制定不同的教学计划。

• 教师阶段Ⅰ：由于接受知识的能力较强，在提出的GTOA中，教师更加注重对出色组整体知识的提高。更具体地说，教师可以尽其所能提高全班的平均知识水平。此外，还需要考虑学生在接受知识方面的差异。因此，出色组的学生可以通过下式获取知识：
  $${\mathbf{x}}_{\text{teacher },i}^{t+1}={\mathbf{x}}_i^t+a\times \left({\mathbf{T}}^t-F\times \left(b\times {\mathbf{M}}^t+c\times {\mathbf{x}}_i^t\right)\right)\text{\hspace{1em}(2)}$$

$${\mathbf{M}}^t=\frac{1}{N}\sum _{i=1}^N{\mathbf{x}}_i^t\text{\hspace{1em}(3)}$$

$$b+c=1\text{\hspace{1em}(4)}$$

其中$t$为当前迭代次数，$N$是学生数量，${\mathbf{x}}_i^t$为学生$i$在时刻$t$的知识，${\mathbf{T}}^t$是教师在时刻$t$的知识，${\mathbf{M}}^t$是时刻$t$小组的平均知识，$F$是决定教师教学成果的教学因子，${\mathbf{x}}_{\text{teacher },i}^{t+1}$是学生$i$在时刻$t$向其老师学习到的知识。$a,b,c$均是$[0,1]$内的随机数。$F$的值通常为1或2。

• 教师阶段Ⅱ：考虑到接受知识的能力较差，根据第二条规则，教师更关注一般组，教师倾向于从个体的角度提高学生的知识水平。因此一般组的学生可以通过下式获取知识：
  $${\mathbf{x}}_{\text{teacher },i}^{t+1}={\mathbf{x}}_i^t+2\times d\times \left({\mathbf{T}}^t-{\mathbf{x}}_i^t\right)\text{\hspace{1em}(5)}$$

其中$d$为$[0,1]$内的随机数。

此外，学生并不能保证在教师阶段一定会获得知识，以最小化问题为例，只有当适应度值降低时才会更新下一时刻的位置。

$${\mathbf{x}}_{\text{teacher },i}^{t+1}=\{\begin{array}{l}{\mathbf{x}}_{\text{teacher },i}^{t+1},f\left({\mathbf{x}}_{\text{teacher },i}^{t+1}\right)<f\left({\mathbf{x}}_i^t\right)\\ {\mathbf{x}}_i^t,f\left({\mathbf{x}}_{\text{teacher, },i}^{t+1}\right)\ge f\left({\mathbf{x}}_i^t\right)\end{array}\text{\hspace{1em}(6)}$$

学生阶段

根据第三条规则，学生阶段也包括Ⅰ和Ⅱ两个阶段。在课余时间，学生可以有两种不同的方式获取知识：自学和与同学交流，可通过下式表达：
$${\mathbf{x}}_{\text{student },i}^{t+1}=\{\begin{array}{l}{\mathbf{x}}_{\text{teacher },i}^{t+1}+e\times \left({\mathbf{x}}_{\text{teacher },i}^{t+1}-{\mathbf{x}}_{\text{teacher },j}^{t+1}\right)+g\times \left({\mathbf{x}}_{\text{teacher },i}^{t+1}-{\mathbf{x}}_i^t\right),f\left({\mathbf{x}}_{\text{teacher },i}^{t+1}\right)<f\left({\mathbf{x}}_{\text{teacher },j}^{t+1}\right)\\ {\mathbf{x}}_{\text{teacher },i}^{t+1}-e\times \left({\mathbf{x}}_{\text{teacher },i}^{t+1}-{\mathbf{x}}_{\text{teacher },j}^{t+1}\right)+g\times \left({\mathbf{x}}_{\text{teacher },i}^{t+1}-{\mathbf{x}}_i^t\right),f\left({\mathbf{x}}_{\text{teacher },i}^{t+1}\right)\ge f\left({\mathbf{x}}_{\text{teacher },j}^{t+1}\right)\end{array}\text{\hspace{1em}(7)}$$

其中$e$和$g$为两个$[0,1]$之间的随机数。${\mathbf{x}}_{\text{student },i}^{t+1}$是学生$i$在时刻$t$通过学生阶段学习到的知识，${\mathbf{x}}_{\text{teacher },j}^{t+1}$是学生$j$在时刻$t$通过老师阶段学习到的知识，学生$j\in \{1,2,...,i-1,i+1,...,N\}$是随机选择的。上式中的第2项和第3项分别表示向其他同学学习和自学。

同样，学生也并不能保证在学生阶段一定会获得知识，以最小化问题为例，只有当适应度值降低时才会更新下一时刻的位置。
$${\mathbf{x}}_i^{t+1}=\{\begin{array}{l}{\mathbf{x}}_{\text{teacher },i}^{t+1},f\left({\mathbf{x}}_{\text{teacher },i}^{t+1}\right)<f\left({\mathbf{x}}_{\text{student },i}^{t+1}\right)\\ {\mathbf{x}}_{\text{student },i}^{t+1},f\left({\mathbf{x}}_{\text{teacher },i}^{t+1}\right)\ge f\left({\mathbf{x}}_{\text{student },i}^{t+1}\right)\end{array}\text{\hspace{1em}(8)}$$

其中${\mathbf{x}}_i^{t+1}$是学生$i$一次学习循环后在时刻$t+1$的知识。

教师分配阶段

基于第四条规则，如何制定一个良好的教师配置机制，对提高学生的知识水平具有十分重要的意义。模仿灰狼优化中的保留三个最优解的思想，教师分配机制可以表达为：

$${\mathbf{T}}^t=\{\begin{array}{ll}{\mathbf{x}}_{\text{first }}^t,& f\left({\mathbf{x}}_{\text{first }}^t\right)\le f\left(\frac{{\mathbf{x}}_{\text{firs }}^t+{\mathbf{x}}_{\text{sscond }}^t+{\mathbf{x}}_{\text{third }}^t}{3}\right)\\ \frac{{\mathbf{x}}_{\text{first }}^t+{\mathbf{x}}_{\text{second }}^t+{\mathbf{x}}_{\text{third }}^t}{3},& f\left({\mathbf{x}}_{\text{first }}^t\right)>f\left(\frac{{\mathbf{x}}_{\text{firs }}^t+{\mathbf{x}}_{\text{second }}^t+{\mathbf{x}}_{\text{thicd }}^t}{3}\right)\end{array}\text{\hspace{1em}(9)}$$
其中${\mathbf{x}}_{\mathrm{f}\mathrm{i}\mathrm{r}\mathrm{s}\mathrm{t}}^{\mathbf{t}},{\mathbf{x}}_{\mathrm{s}\mathrm{e}\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{d}}^{\mathbf{t}},{\mathbf{x}}_{\mathrm{t}\mathrm{h}\mathrm{i}\mathrm{r}\mathrm{d}}^{\mathbf{t}}$分别为第一优、第二优和第三优学生，为了加快算法的收敛，出色组和一般组共用相同的老师。

GTOA实现

下面给出GTOA的实现步骤。

Step1：初始化

(1.1)初始化参数。这些参数包括最大评估次数$T_{max}$，当前评估次数$T_{current}(T_{current}=0)$，种群大小$N$，决策变量的上下界$\mathbf{u}$和$\mathbf{l}$，维度$D$和适应度函数$f(\cdot )$。

(1.2)初始化种群。根据以上初始参数随机生成种群${\mathbf{X}}^{\mathbf{t}}$:
$${\mathbf{X}}^t={\left[{\mathbf{x}}_1^t,{\mathbf{x}}_2^t,\dots ,{\mathbf{x}}_N^t\right]}^{\mathrm{T}}=\left[\begin{array}{cccc}{x}_{1,1}^t& x_{1,2}^t& \dots & x_{1,D}^t\\ x_{2,1}^t& x_{2,2}^t& \dots & x_{2,D}^t\\ ⋮& ⋮& & ⋮\\ x_{N,1}^t& x_{N,2}^t& \dots & x_{N,D}^t\end{array}\right]\text{\hspace{1em}(10)}$$

$$x_{i,j}^t=l_i+\left(u_i-l_i\right)\times \kappa \text{\hspace{1em}(11)}$$

其中$\kappa$为$[0,1]$之间的随机数。

Steo2：种群评估。

计算个体的适应度值，选出最优解${\mathbf{G}}^t$，更新当前函数评估次数$T_{current}$：
$$T_{current}=T_{current}+N\text{\hspace{1em}(12)}$$

Step3：终止准则

如果当前评估次数$T_{current}$大于最大评估次数$T_{max}$，终止算法并输出最优解${\mathbf{G}}^t$，否则跳转至Step4。

Step4：教师分配阶段

选出三个最优解，根据公式(9)计算${\mathbf{T}}^t$。

Step5：能力分组阶段

基于适应度值将种群分成两个组，最好的一半个体组成出色组${\mathbf{X}}_{\text{good }}^t$，剩余的个体组成一般组${\mathbf{X}}_{\text{bad }}^t$。这两组共用相同的老师。

Step6：教师阶段和学生阶段

(6.1)对于${\mathbf{X}}_{\text{good }}^t$组，基于公式(2),(3),(4)和(6)实现教师阶段，再根据(7)和(8)执行学生阶段。最终获取新的${\mathbf{X}}_{\text{good }}^{t+1}$。

(6.2)对于${\mathbf{X}}_{\text{bad }}^t$组，基于公式(5)和(6)实现教师阶段，再根据(7)和(8)执行学生阶段。最终获取新的${\mathbf{X}}_{\text{bad }}^{t+1}$。

Step7：构建种群

将${\mathbf{X}}_{\text{good }}^{t+1}$和${\mathbf{X}}_{\text{bad }}^{t+1}$组成一个新的种群${\mathbf{X}}^{t+1}$。

Step8：种群评估

计算个体的适应度值，选出最优解${\mathbf{G}}^t$，更新当前函数评估次数$T_{current}$：
$$T_{current}=T_{current}+2N+1\text{\hspace{1em}(13)}$$

然后执行Step3。

下图为上述过程的流程图。