Eigen库下载安装并配置到VS

1.简介：

Eigen是一个高层次的C ++库，有效支持线性代数，矩阵和矢量运算，数值分析及其相关的算法。

Eigen适用范围广，支持包括固定大小、任意大小的所有矩阵操作，甚至是稀疏矩阵；支持所有标准的数值类型，并且可以扩展为自定义的数值类型；支持多种矩阵分解及其几何特征的求解；它不支持的模块生态系统 [2] 提供了许多专门的功能，如非线性优化，矩阵功能，多项式解算器，快速傅立叶变换等。Eigen支持多种编译环境，开发人员对库中的实例在多种编译环境下经过测试，以保证其在不同编译环境下的可靠性和实用性。

2.下载：

1.Eigen官网下载。（不知为什么，我电脑一只打不开官网！）

2.GitHub上下载。

3.百度云盘下载.提取码：d0jk

3.安装：

首先，将压缩包解压到本地随意一个盘中。

然后，打开VS，我安装的是VS2010,新建一个工程，鼠标放到工程名上点击右键，选择属性：

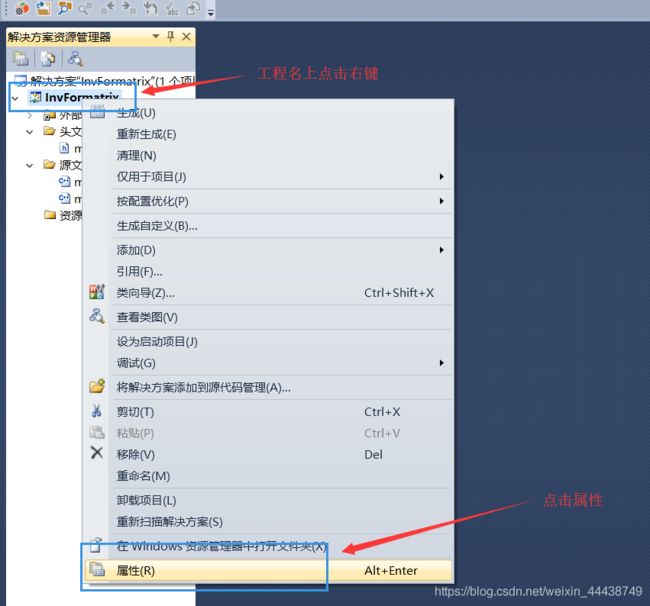
最后：

4.测试：

#include <iostream>
#include <Eigen/SVD>
#include <Eigen/Core>


using namespace std;


// 利用Eigen库，采用SVD分解的方法求解矩阵伪逆，默认误差er为0
Eigen::MatrixXd pinv_eigen_based(Eigen::MatrixXd & origin, const float er = 0) {
	// 进行svd分解
	Eigen::JacobiSVD<Eigen::MatrixXd> svd_holder(origin,
		Eigen::ComputeThinU |
		Eigen::ComputeThinV);
	// 构建SVD分解结果
	Eigen::MatrixXd U = svd_holder.matrixU();
	Eigen::MatrixXd V = svd_holder.matrixV();
	Eigen::MatrixXd D = svd_holder.singularValues();

	// 构建S矩阵
	Eigen::MatrixXd S(V.cols(), U.cols());
	S.setZero();

	for (unsigned int i = 0; i < D.size(); ++i) {

		if (D(i, 0) > er) {
			S(i, i) = 1 / D(i, 0);
		} else {
			S(i, i) = 0;
		}
	}
	return V * S * U.transpose();
}



int main() {

	Eigen::MatrixXd B(7,7);
	B<<1,2,3,4,5,6,7,
		1,2,3,4,5,6,7,
		1,2,3,4,5,6,7,
		1,2,3,4,5,6,7,
		1,2,3,4,5,6,7,
		1,2,3,4,5,6,7,
		1,2,3,4,5,6,7;

	// 打印矩阵B的伪逆矩阵
	cout<<B<<endl;

	cout << "矩阵B的伪逆为：" << endl;

	cout << pinv_eigen_based(B) << endl;

	getchar();
}

打印结果：

MATLAB仿真结果：

关于一些使用方法，可以参照：Eigen库使用指南.