Python数据分析 利用NetworkX绘制网络图

1. NetworkX 概述

NetworkX 是一个用Python语言开发的图论与复杂网络建模工具，内置了常用的图与复杂网络分析算法，可以方便的进行复杂网络数据分析、仿真建模等工作。networkx支持创建简单无向图、有向图和多重图；内置许多标准的图论算法，节点可为任意数据；支持任意的边值维度，功能丰富。主要用于创造、操作复杂网络，以及学习复杂网络的结构、动力学及其功能。用于分析网络结构，建立网络模型，设计新的网络算法，绘制网络等等。

2. NetworkX的安装

pip install networkx -i http://pypi.douban.com/simple --trusted-host pypi.douban.com

3. NetworkX基础知识

创建图
可以利用networkx创建四种图： Graph 、DiGraph、MultiGraph、MultiDiGraph，分别为无多重边无向图、无多重边有向图、有多重边无向图、有多重边有向图。

import network as nx 
G = nx.Graph()
G = nx.DiGraph()
G = nx.MultiGraph()
G = nx.MultiDiGraph()

网络图的加点和加边

import networkx as nx
import matplotlib.pyplot as plt

G = nx.DiGraph()
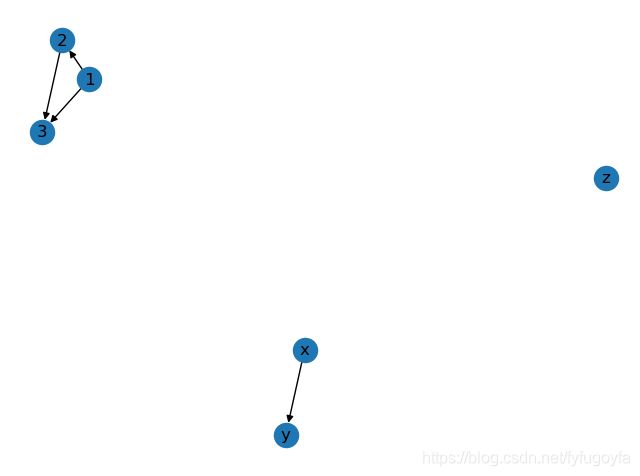
G.add_node('z')     # 添加节点z
G.add_nodes_from([1, 2, 3])   # 添加节点 1 2 3
G.add_edge('x', 'y')          # 添加边  起点为x  终点为y
G.add_edges_from([(1, 2), (1, 3), (2, 3)])   # 添加多条边

# 网络图绘制与显示
nx.draw(G, with_labels=True)
plt.show()

运行结果如下：

为了让网络图更好看可以调节nx.draw()方法里的参数

nx.draw(G, pos=nx.random_layout(G), node_color = 'b', edge_color = 'r', with_labels = True, font_size =18, node_size =20)

• G：待绘制的网络图G
• node_size：指定节点的尺寸大小(默认是300)
• node_color: 指定节点的颜色 (可以用字符串简单标识颜色，例如’r’为红色，'g’为绿色这样)
• node_shape: 节点的形状（默认是圆形，用字符串’o’标识）
• alpha: 透明度 (默认是1.0，不透明，0为完全透明)
• width: 边的宽度 (默认为1.0)
• edge_color: 边的颜色(默认为黑色)
• style: 边的样式(默认为实现，可选： solid | dashed | dotted | dashdot
• with_labels：节点是否带标签
• font_size: 节点标签字体大小
• font_color: 节点标签字体颜色（默认为黑色）

运用布局：
circular_layout：节点在一个圆环上均匀分布
random_layout：节点随机分布
shell_layout：节点在同心圆上分布
spring_layout：用Fruchterman-Reingold算法排列节点（样子类似多中心放射状）
spectral_layout：根据图的拉普拉斯特征向量排列节点

绘制网络图实例如下：

import networkx as nx
import matplotlib.pyplot as plt

# 初始化一个有向图对象
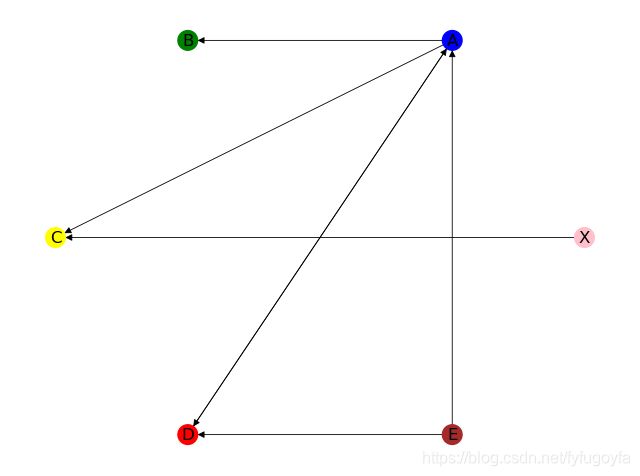
DG = nx.DiGraph()
DG.add_node('X')
# 添加节点   传入列表
DG.add_nodes_from(['A', 'B', 'C', 'D', 'E'])
print(f'输出图的全部节点：{DG.nodes}')
print(f'输出节点的数量：{DG.number_of_nodes()}')
# 添加边  传入列表  列表里每个元素是一个元组  元组里表示一个点指向另一个点的边
DG.add_edges_from([('A', 'B'), ('A', 'C'), ('A', 'D'), ('D', 'A'), ('E', 'A'), ('E', 'D')])
DG.add_edge('X', 'C')
print(f'输出图的全部边:{DG.edges}')
print(f'输出边的数量：{DG.number_of_edges()}')
# 可自定义节点颜色
colors = ['pink', 'blue', 'green', 'yellow', 'red', 'brown']
# 运用布局
pos = nx.circular_layout(DG)
# 绘制网络图
nx.draw(DG, pos=pos, with_labels=True, node_size=200, width=0.6, node_color=colors)
# 展示图片
plt.show()

运行效果如下：

输出图的全部节点：['X', 'A', 'B', 'C', 'D', 'E']
输出节点的数量：6
输出图的全部边:[('X', 'C'), ('A', 'B'), ('A', 'C'), ('A', 'D'), ('D', 'A'), ('E', 'A'), ('E', 'D')]
输出边的数量：7

4. 利用NetworkX实现关联类分析

利用 soccer.csv 中的数据，使用 Python 的 NetworkX 包按要求进行绘图。

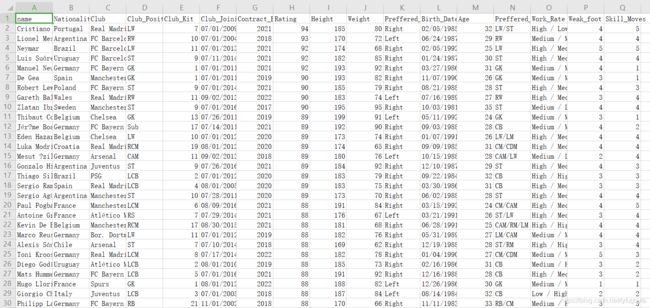
(1) 提取数据
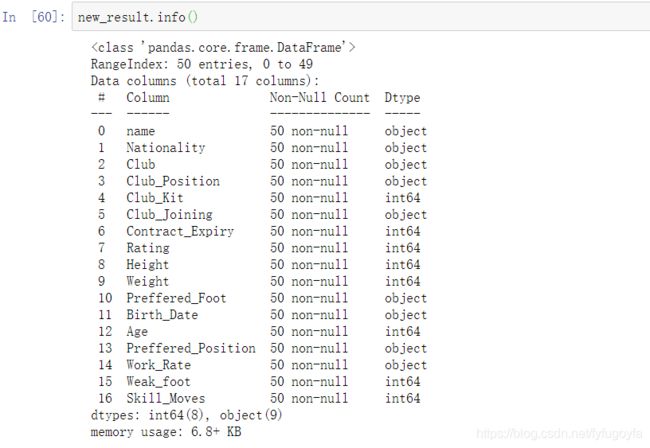
统计不同俱乐部（Club）的球员数量，从球员最多的五个俱乐部抽取 50 名球员信息(球员数量最多的俱乐部抽取 30 名，剩下 4 个俱乐部各抽取 5 名)构成新的 DataFrame，打印其info()。

import pandas as pd

df = pd.read_csv('soccer.csv', encoding='gbk')
data = df['Club'].value_counts()
# 球员人数最多的5个俱乐部
clubs = list(data.index[:5])

# 球员数量最多的俱乐部抽取30名
df1 = df[df['Club'] == clubs[0]].sample(30, axis=0)
# 剩下4个俱乐部各抽取5名
df2 = df[df['Club'] == clubs[1]].sample(5, axis=0)
df3 = df[df['Club'] == clubs[2]].sample(5, axis=0)
df4 = df[df['Club'] == clubs[3]].sample(5, axis=0)
df5 = df[df['Club'] == clubs[4]].sample(5, axis=0)

# 合并多个DataFrame
result = pd.concat([df1, df2, df3, df4, df5], axis=0, ignore_index=True)
# 打乱DataFrame顺序
new_result = result.sample(frac=1).reset_index(drop=True)
# new_result.info()
# 抽样的数据保存到excel
new_result.to_excel('samples.xlsx')

Jupyter Notebook运行环境里打印其info()，结果如下：

(2) 画网络图
在提取出的数据的基础上，通过判断球员是否属于同一俱乐部，绘出随机分布网络图、Fruchterman-Reingold 算法排列节点网络图与同心圆分布网络图。尽可能让网络图美观，如为属于同一俱乐部的节点设置相同的颜色。

将每个球员当作网络图中一个节点，计算节点之间的连通关系，同属一个俱乐部则连通。

import pandas as pd

df = pd.read_excel('samples.xlsx')
df = df.loc[::, ['Name', 'Club']]
datas = df.values.tolist()
name = [datas[i][0] for i in range(len(datas))]
nodes = [str(i) for i in range(len(datas))]
club = [datas[i][1] for i in range(len(datas))]
# print(nodes)
df = pd.DataFrame({'姓名': name, '节点编号': nodes, '所属俱乐部': club})
df.to_csv('nodes_info.csv')
with open('record.txt', 'w') as f:
    for i in range(len(nodes)):
        for j in range(i, len(nodes) - 1):
            if datas[i][1] == datas[j+1][1]:      # 属于同一俱乐部
                f.write(f'{nodes[i]}-{nodes[j + 1]}-{datas[i][1]}' + '\n')

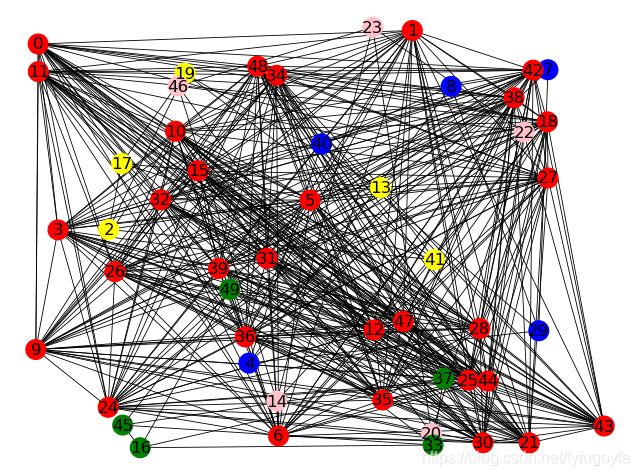
随机分布网络图

import networkx as nx
import matplotlib.pyplot as plt
import pandas as pd

s = ['pink', 'blue', 'green', 'yellow', 'red']
df = pd.read_csv('nodes_info.csv')['所属俱乐部']
items = df.values
node_colors = []
# 5个俱乐部   属于同一个俱乐部的节点设置相同颜色
for item in items:
    if item == 'Free Agents':
        node_colors.append('red')
    elif item == 'Manchester Utd':
        node_colors.append('yellow')
    elif item == 'Leicester City':
        node_colors.append('blue')
    elif item == 'Málaga CF':
        node_colors.append('green')
    elif item == 'CA Osasuna':
        node_colors.append('pink')


DG = nx.MultiGraph()
DG.add_nodes_from([str(i) for i in range(0, 50)])
DG.nodes()

with open('record.txt', 'r') as f:
    con = f.read().split('\n')

edges_list = []
for i in con[:-1]:
    edges_list.append(tuple(i.split('-')[:2]))
print(edges_list)
DG.add_edges_from(edges_list)
DG.edges()
# 随机分布网络图
pos = nx.random_layout(DG)
nx.draw(DG, pos, with_labels=True, node_size=200, width=0.6, node_color=node_colors)
plt.show()

运行效果如下：

Fruchterman-Reingold 算法排列节点网络图

import networkx as nx
import matplotlib.pyplot as plt
import pandas as pd

df = pd.read_csv('nodes_info.csv')['所属俱乐部']
items = df.values
node_colors = []
# 5个俱乐部   属于同一个俱乐部的节点设置相同颜色
for item in items:
    if item == 'Free Agents':
        node_colors.append('red')
    elif item == 'Manchester Utd':
        node_colors.append('yellow')
    elif item == 'Leicester City':
        node_colors.append('blue')
    elif item == 'Málaga CF':
        node_colors.append('green')
    elif item == 'CA Osasuna':
        node_colors.append('pink')


DG = nx.MultiGraph()
DG.add_nodes_from([str(i) for i in range(0, 50)])
DG.nodes()

with open('record.txt', 'r') as f:
    con = f.read().split('\n')

edges_list = []
for i in con[:-1]:
    edges_list.append(tuple(i.split('-')[:2]))

print(edges_list)
DG.add_edges_from(edges_list)
# DG.edges()
# Fruchterman-Reingold 算法排列节点网络图
pos = nx.spring_layout(DG)
nx.draw(DG, pos, node_size=10, width=0.6, node_color=node_colors, )
plt.show()

运行效果如下：

同心圆分布网络图

import networkx as nx
import matplotlib.pyplot as plt
import pandas as pd

df = pd.read_csv('nodes_info.csv')['所属俱乐部']
items = df.values
node_colors = []
# 5个俱乐部   属于同一个俱乐部的节点设置相同颜色
for item in items:
    if item == 'Free Agents':
        node_colors.append('red')
    elif item == 'Manchester Utd':
        node_colors.append('yellow')
    elif item == 'Leicester City':
        node_colors.append('blue')
    elif item == 'Málaga CF':
        node_colors.append('green')
    elif item == 'CA Osasuna':
        node_colors.append('pink')


DG = nx.MultiGraph()
DG.add_nodes_from([str(i) for i in range(0, 50)])
DG.nodes()

with open('record.txt', 'r') as f:
    con = f.read().split('\n')

edges_list = []
for i in con[:-1]:
    edges_list.append(tuple(i.split('-')[:2]))

print(edges_list)
DG.add_edges_from(edges_list)
# DG.edges()
# 同心圆分布网络图
pos = nx.shell_layout(DG)
nx.draw(DG, pos, with_labels=True, node_size=200, width=0.6, node_color=node_colors, )
plt.show()

运行效果如下：