【强化学习】Q Learning

原文链接：https://www.yuque.com/yahei/hey-yahei/rl-q_learning

参考：

• 机器学习深度学习（李宏毅） - Q Learning
• 机器学习深度学习（李宏毅） - Q Learning Advanced Tips
• 机器学习深度学习（李宏毅） - Q Learning Continuous Action

基本形式

Q Learning是一种value-based的RL算法，value-based算法旨在训练一个Critic（记为$$V^{\pi }$$），它与某个Actor绑定，能够根据状态$$s$$（和采取的动作$$a$$）预测出Actor接下来能累计获得多少奖励。

只考虑状态

首先考虑最简单的value-based算法，它只根据状态$$s$$来预测未来的累计奖励——

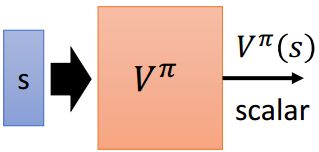
如何训练这样一个Critic呢？这里列出两种常用的训练方法——

1. 蒙特卡洛（Monte-Carlo, MC）
   用完整的episode进行训练
   
2. 时间差分（Temporal-Difference, TD）
   用相邻两个状态的差值进行训练
   

这两个方法各有优劣，

• MC比较精确，
  TD比较稳定
• MC的结果有较大的方差，而且如果episode很长，那么在训练时会有困难；
  TD的结果方差较小，但$$V^{\pi }(s_{t+1})$$的预测不一定准确，以其为标准来训练、更新也说不上合理
• MC会关注不同状态的相关性，
  TD则不关注（都合理，但也都不完美）
  举个例子，
  
  很好理解，8个episode，无论是MC还是TD，都有$$V^{\pi }(s_b)=3/4$$；
  对于$$V^{\pi }(s_a)$$就比较麻烦了，$$V_{MC}^{\pi }(s_a)=0,V_{TD}^{\pi }(s_a)=V_{TD}^{\pi }(s_b)+r=3/4$$，相差甚远；
  那么是MC合理还是TD合理呢？其实都合理的，考虑第一个episode，
  • MC考量了整个episode的情况，认为是因为$$s_a$$的出现，导致了后续的KaTeX parse error: Expected group after '_' at position 2: s_̲没能拿到奖励；
  • TD则认为$$s_b$$没能拿到奖励只不过是个巧合，并不一定是$$s_a$$的出现带来的影响

综合状态和动作

前述的两种算法只考虑了状态$$s$$对后续累计奖励的影响，而Q Learning在此基础上还额外考虑了采取的动作$$a$$的影响。Q Learning有两种表现形式——

1. 以状态$$s$$和动作$$a$$为输入，直接预测在状态$$s$$下采取动作$$a$$之后的累计奖励（如左图）；
2. 以状态$$s$$为输入，预测在状态$$s$$下采取不同动作$$a$$之后的累计奖励（如右图），这种情况下要求可采取的动作是有限的（当然，也有一些解决方案）

对于Q Learning来说，并不需要独立的Actor，这是因为Critic应该给出了所有动作的未来累计价值，选择未来累计价值最高的一个动作即可，相当于隐含了Policy。
$${\pi }^{\prime }(s)=\arg \underset{a}{\max }{Q}^{\pi }(s,a)$$
训练过程可以用下图概括，以最大化Q为目标，用TD或MC算法迭代训练——
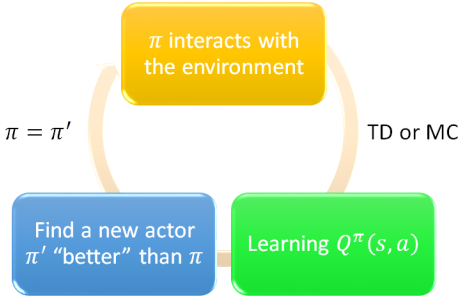
（Q Learning训练过程示意）

如果Q Learning跟深度学习结合起来，那么就称为Deep Q-learning Network, DQN。

三点改进

在使用TD算法训练Q Learning模型时，存在一个问题，如果频繁对产生目标$$Q^{\pi }\left(s_{t+1},\pi (s_{t+1})\right)$$的模型$$\pi$$进行更新，使得回归出来的$$Q^{\pi }\left(s_t,a_t\right)$$逼近$$r_t+{\mathrm{Q}}^{\pi }\left(s_{t+1},\pi \left(s_{t+1}\right)\right)$$，那么训练过程很容易不稳定（因为对于同样的状态和动作，目标却一直在发生变化）。
因此可以引入一个独立的目标网络（Target Network），被训练的网络每迭代一定步数之后再将权重应用到目标网络上去，以此产生相对稳定的目标，使得训练过程变为稳定。

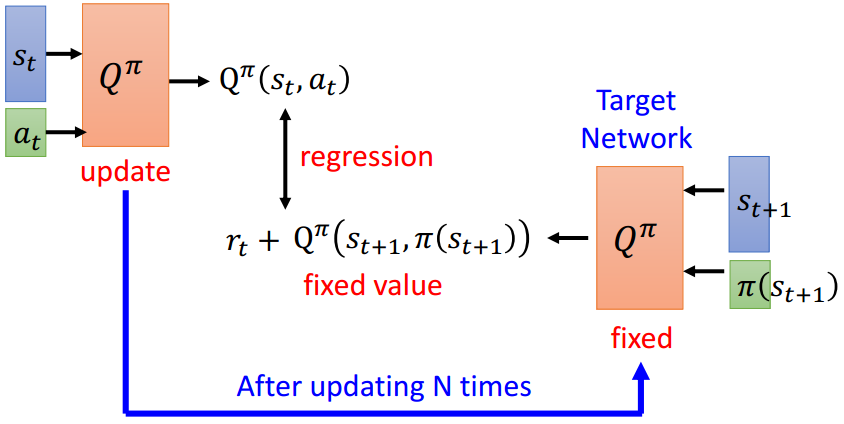
与policy-based算法一样，Q Learning也面临着探索（Exploration）的问题，为了避免$$Q^{\pi }$$对于某个状态$$s$$倾向于对某个动作$$a$$产生更大的Q值，需要采取一些措施来鼓励网络对其他动作进行探索。比如，

• Epsilon Greedy
  以一定概率随机挑选动作而非选取Q值最大的动作，通常训练早期倾向于探索，后期能产生比较准确而稳定Q值之后转而更多依靠已学的知识。所以会在训练初期使用一个较大的$$ϵ$$，随着训练过程的推进逐渐衰减
  $$a=\{\begin{array}{cc}\arg {\max }_{a}Q(s,a),& \text{ with probability }1-\epsilon \\ \text{ random, }& \text{ otherwise }\end{array}$$
• Boltzmann Exploration
  模仿softmax为不同动作的Q值进行规范化，产生一个概率分布，按概率随机抽取所要执行的动作
  $$P(a|s)=\frac{\exp (Q(s,a))}{{\sum }_a\exp (Q(s,a))}$$

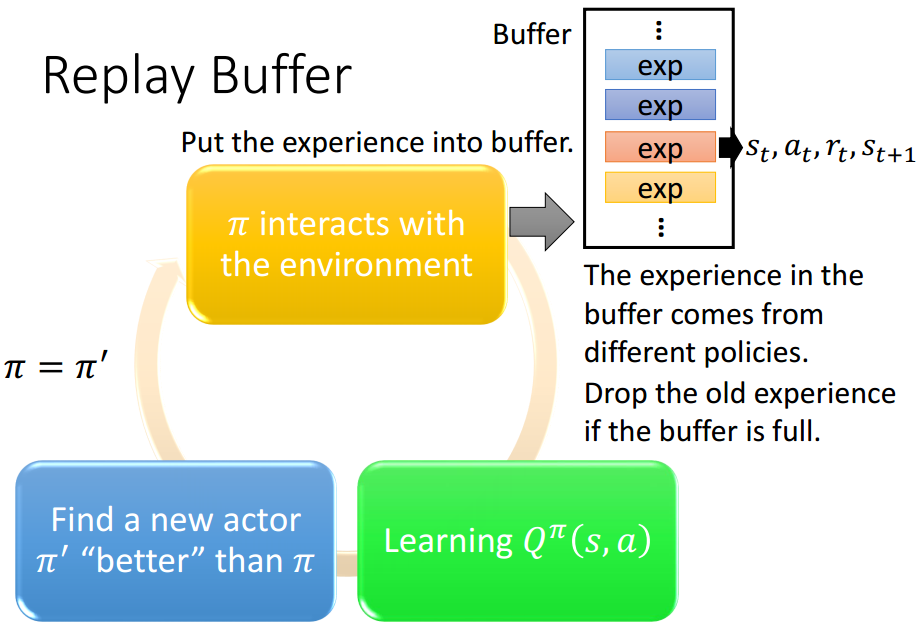
每次交互结果都只用来训练一次似乎有些浪费，可以用一个缓冲区（Replay Buffer）来记录早前的交互状况$$(s_t,a_t,r_t,s_{t+1})$$，每次从缓冲区中随机抽取一些经历构成batch来进行训练。虽然这些经历来自于不同的policies，甚至可能是差异比较大的policies，但考虑到状态、动作、奖励、下一个状态是客观存在的，跟policies本身无关，所以影响并不大。这种方法通常称为经验回放（Experience Replay）。

DQN的一些进展

Double DQN

论文：

• 《Double Q-learning (NIPS2010)》
• 《Deep Reinforcement Learning with Double Q-Learning (AAAI2016))》

$$Q\left(s_t,a_t\right)⟷r_t+\underset{a}{\max }Q\left(s_{t+1},a\right)$$
观察Q Learning的目标，可以发现$$\underset{a}{\max }Q\left(s_{t+1},a\right)$$很容易被高估，从而导致整个目标被高估，恶性循环，Q值会存在一直被高估的现象。
为了解决这一问题，可以引入一个新的DQN（公式中的$$Q^{\prime }$$），用于独立地估计下一个state的Q值，
$$Q\left(s_t,a_t\right)⟷r_t+Q^{\prime }\left(s_{t+1},\arg \underset{a}{\max }Q\left(s_{t+1},a\right)\right)$$
其实就是个冗余设计，两个DQN之间互相监督，减少高估情况的发生，

• 如果$$Q$$可能出现高估，那么$$Q^{\prime }$$会重新估计一个相对准确的Q值
• 如果$$Q^{\prime }$$可能出现高估，那么$$Q$$也有可能不采取会被高估的那个action
• $$Q$$和$$Q^{\prime }$$同时高估的可能性就远低于单一个$$Q$$高估的可能性

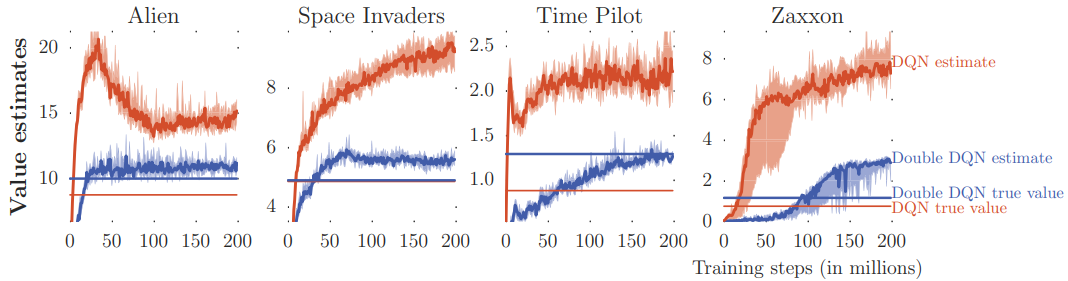
（Double DQN的效果）

Dueling DQN

论文：《Dueling Network Architectures for Deep Reinforcement Learning (2015)》

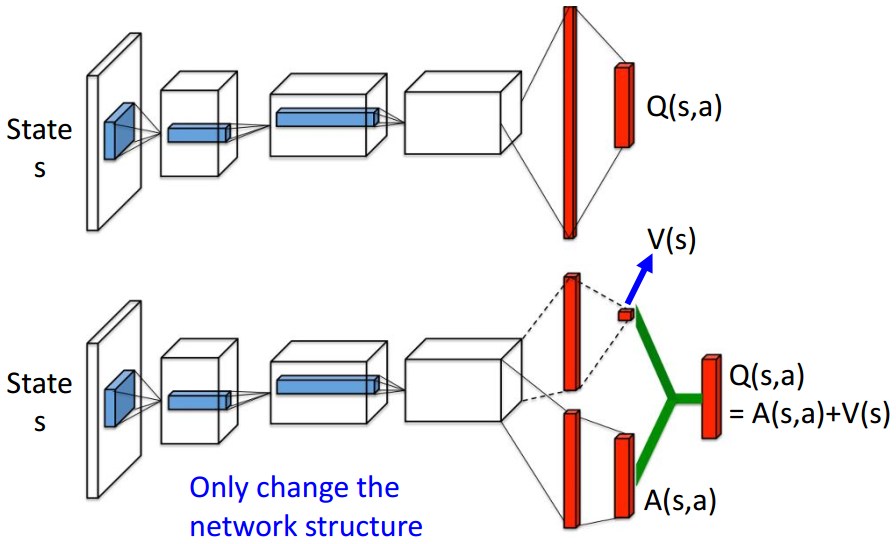
（上：DQN； 下：Dueling DQN）

Dueling DQN不再直接输出Q值，而是由两个子分支分别输出state的Q值、在该state下各个action的Q值增量，最后广播相加得到在该state下各个action的实际Q值。
$$Q(s,a)=A(s,a)+V(s)$$
通常会约束$$\sum A(s,a_i)=0$$，该约束在实现上也非常简单，直接对分支的输出做去均值的处理，然后再进行$$Q(s,a)$$的计算就行。该约束使得$$V(s)$$输出恰好为$$Q(s,a)$$的均值，在训练过程中即使某些action没有在episode中出现，Dueling DQN也有可能倾向于更新均值$$V(s)$$，此时这些没有出现的action的Q值也会随之更新。

Prioritized Replay

论文：《Prioritized Experience Replay (ICLR2016)》
为Experience Buffer加一个优先级，增加对以往TD误差较大的样本的抽样概率。

Multi-step

MC和TD的一个折中版本，MC考虑整个episode，TD只考虑相邻的两次决策，Multi-step则考虑连续的N次决策。

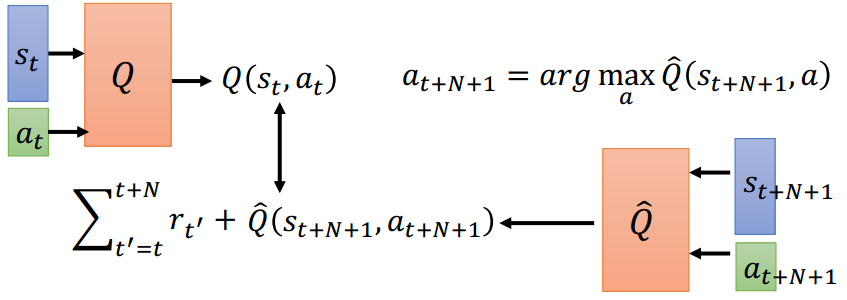
Noisy Net

论文：（两篇论文主体思路一致，只是加噪方式有点差别）

• 《Parameter Space Noise for Exploration (ICLR2018)》
• 《Noisy Networks for Exploration (ICLR2018)》

之前讲过Epsilon Greedy的随机采取action的技巧，但论文认为这种Exploration不太合理，这种情况下面对同一个state很可能采取不同的action，这在实际中就不应该存在的，有可能会让模型点歪了技能树，从此越走越远（虽然在这条技术路线上可能还是会逐步提升，但并不能达到最理想的效果）；因此提出，对参数进行加噪要比对action进行加噪更加合理。
$$\begin{gathered} Q(s,a)\stackrel{\text{Add Noise}}{}\tilde{Q}(s,a) \\ a=\arg \underset{a}{\max }\tilde{Q}(s,a) \end{gathered}$$
加噪的方式有很多，比如最简单的给一个高斯噪声；
另外，在同一个episode中，噪声应当保持一致

Distributional Q-function

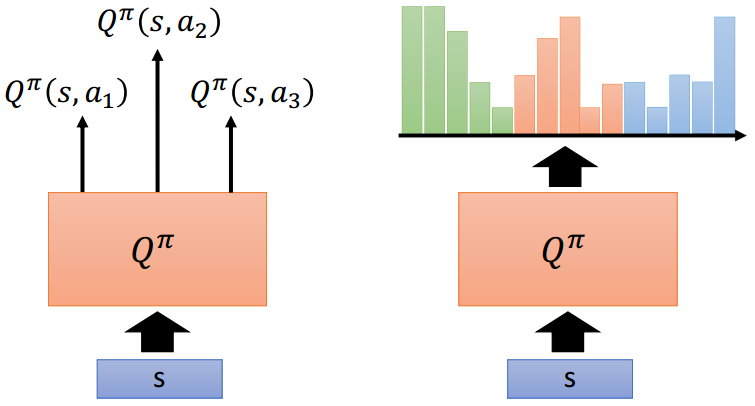
让$$Q^{\pi }$$不再简单输出一个scalar，而是输出一个信息更加丰富的分布。
比如将原本的3输出神经网络，改为15输出的神经网络，每五个一组作为action的Q值分布（相当于一个5bins的直方图）。

Rainbow实验探究

论文：《Rainbow: Combining Improvements in Deep Reinforcement Learning (AAAI2018)》
对前述的技术进行一系列的实验比较，来说明他们的有效性。
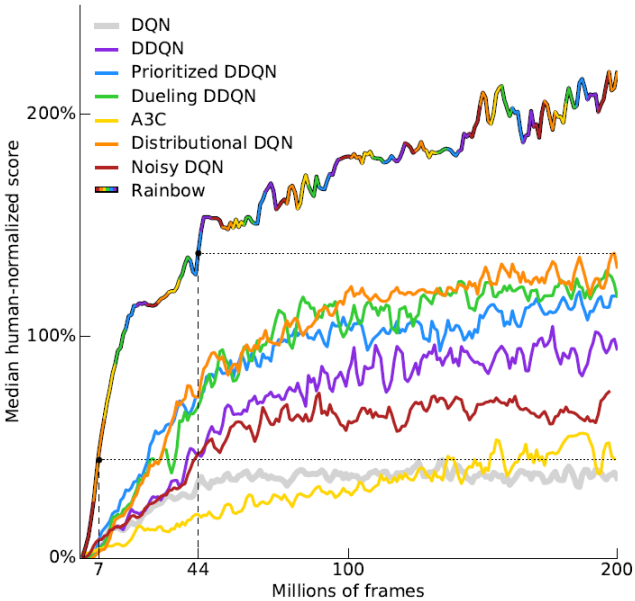
（单一技巧与Rainbow的比较）
（注意Multi-step技巧其实是A3C的一部分）

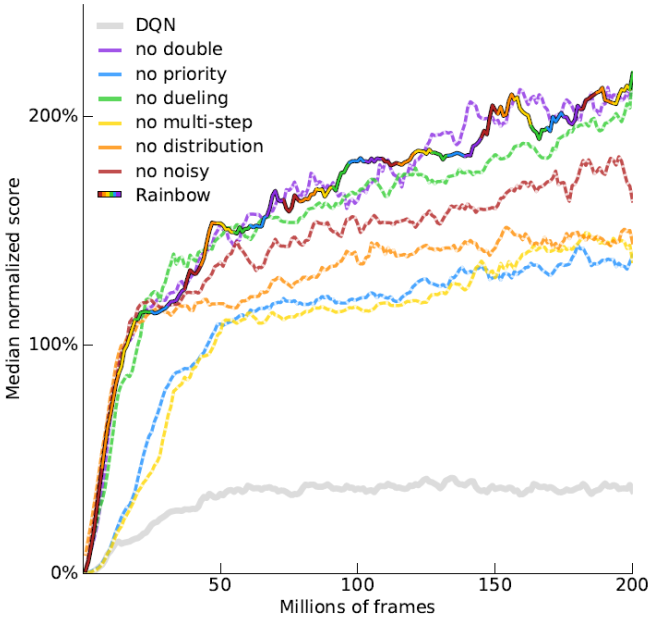
（Ablation studies）

值得注意的是，从图中我们看到即使去掉double技术，对rainbow似乎没有什么影响，论文中给出的解释是，distribution已经很好的解决了Q值高估的问题，所以double就显得不那么必要了。

处理非离散的动作

Q Learning通常只能处理离散的、可穷举的action，但现实世界中有很多非离散的情况，比如自动驾驶的汽车应该转过几度，或者控制机械手的舵机应当转过几度等等。
为了让Q Learning可以处理非离散的动作，有以下一些处理的方法：

1. 对非离散的动作进行采样
   比如转向0-90°，离散成$$\{0,10°,20°,30°,40°,50°,60°,70°,80°,90°\}$$的动作选项；
   （是不是也可以不暴力离散化，而是转换以原始值为均值的正态分布呢？）
2. 用梯度上升法更新动作$$a$$
   但训练起来非常麻烦，你除了需要优化$$Q^{\pi }$$，还得花功夫去优化$$a$$本身，而且还不容易找到全局最优的情况
3. 改造$$Q^{\pi }$$的输出，使其隐含动作$$a$$，比如
   
   $$Q(s,a)=-{\left(a-\mu (s)\right)}^T\Sigma (s)\left(a-\mu (s)\right)+V(s)$$
   这里$$a$$是一个vector，由于有$${\left(a-\mu (s)\right)}^T\Sigma (s)\left(a-\mu (s)\right)>0$$（噫？为啥？？），那么实际上取$$a=\mu (s)$$即可以使Q值最大化。具体在训练过程中会用到一些trick，比如如何保证$$\Sigma (s)$$为正定矩阵等等，此处也就不再赘述