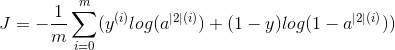Planar data classification with one hidden layer-1

版权为吴恩达老师所有，参考Koala_Tree的博客，部分根据自己实践添加

使用google翻译，部分手工翻译

你可能需要的参考资料https://pan.baidu.com/s/1BJX6XXi3DOBcd7iAuinfKQ

具有一个隐藏层的平面数据分类

1 - 包

让我们首先导入在此任务期间您需要的所有包。
- numpy是使用Python进行科学计算的基础包。
- sklearn为数据挖掘和数据分析提供简单有效的工具。 
- matplotlib是一个用Python绘制图形的库。
- testCases_v2提供了一些测试示例来评估函数的正确性
- planar_utils提供了在此赋值中使用的各种有用函数

# encoding:utf-8
import numpy as np 
import matplotlib.pyplot as plt 
from testCases_v2 import *
import sklearn
import sklearn.datasets
import sklearn.linear_model
from planar_utils import plot_decision_boundary,sigmoid,load_planar_dataset,load_extra_datasets

np.random.seed(1)

tips:
1.planar_utils.py文件pylint可能在cmap=plt.cm.Spectral处会报错,无需在意

2 - 数据集

首先，让我们获取您将要处理的数据集。以下代码将“flower”2级数据集加载到变量X和Y。

X,Y=load_planar_dataset()

使用matplotlib可视化数据集。数据看起来像一个“花”，有一些红色（标签y = 0）和一些蓝色（y = 1）点。您的目标是构建适合此数据的模型。

plt.scatter(X[0, :], X[1, :], c=Y.reshape(400,), s=40, cmap=plt.cm.Spectral)
plt.show()

你有：
- 一个包含你的特征（x1，x2）的numpy-array（矩阵）X 
- 一个包含你的标签的numpy-array（vector）Y（红色：0，蓝色：1）。

让我们首先更好地了解我们的数据是什么样的。

练习：你有多少训练样例？此外，什么是shape变量X和Y？

提示：你如何得到一个numpy数组的形状？（help）

shape_X=X.shape 
shape_Y=Y.shape
m=X.shape[1]

3 - 简单的Logistic回归

在构建完整的神经网络之前，让我们先看看逻辑回归如何解决这个问题。您可以使用sklearn的内置函数来执行此操作。运行以下代码以在数据集上训练逻辑回归分类器。

clf=sklearn.linear_model.LogisticRegressionCV()
clf.fit(X.T,Y.T.flatten())

您现在可以绘制这些模型的决策边界。运行以下代码。

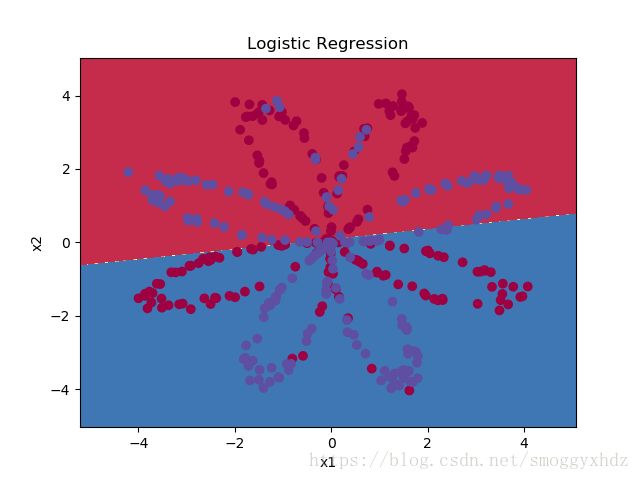
plot_decision_boundary(lambda x:clf.predict(x),X,Y.flatten())
plt.title("Logistic Regression")
plt.show()

LR_predictions=clf.predict(X.T)
print("Accuracy of logistic regression: %d" %float((np.dot(Y,LR_predictions)+np.dot(1-Y,1-LR_predictions))/float(Y.size)*100)+"%"+"(percentage of correctly labelled datapoints)")

tips:
1.要把Y降维,用".flatten()"

解释：数据集不是线性可分的，因此逻辑回归效果不佳。希望神经网络能做得更好。我们现在试试吧！

4 - 神经网络模型

Logistic回归在"花"数据集上效果不佳。您将使用单个隐藏层训练神经网络。

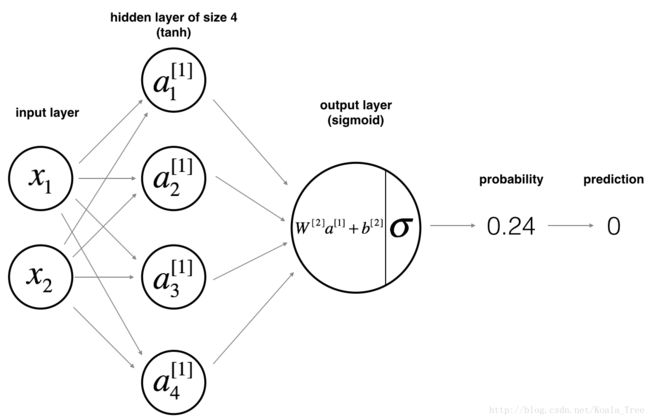
这是我们的模型：

数学上：

举个例子：

鉴于所有示例的预测，您还可以按如下方式计算成本J：

提醒：构建神经网络的一般方法是：
1.定义神经网络结构（输入单元数，隐藏单元数等）。 
2.初始化模型的参数
3.循环：
- 实现正向传播
- 计算损失
- 实现逆向传播以获得梯度
- 更新参数（梯度下降）

您经常构建辅助函数来计算步骤1-3，然后将它们合并到我们调用的一个函数中nn_model()。一旦构建nn_model()并学习了正确的参数，就可以对新数据进行预测。

4.1 - 定义神经网络结构

练习：定义三个变量：
- n_x：输入图层
的大小 - n_h：隐藏图层的大小（设置为4） 
- n_y：输出图层的大小

提示：使用X和Y的形状来查找n_x和n_y。此外，隐藏层大小为4。

def layer_sizes(X,Y):
    n_x=X.shape[0]
    n_h=4
    n_y=Y.shape[0]
    return (n_x,n_h,n_y)

X_assess,Y_assess=layer_sizes_test_case()
(n_x,n_h,n_y)=layer_sizes(X_assess,Y_assess)
print("The size of the input layer is: n_x = " + str(n_x))
print("The size of the hidden layer is: n_h = " + str(n_h))
print("The size of the output layer is: n_y = " + str(n_y))

4.2 - 初始化模型的参数

练习：实现功能initialize_parameters()。

说明：
- 确保您的参数尺寸正确。如果需要，请参阅上面的神经网络图。
- 您将使用随机值初始化权重矩阵。 
- 使用：np.random.randn(a,b) * 0.01随机初始化形状矩阵（a，b）。
- 您将偏置向量初始化为零。 
- 使用：np.zeros((a,b))用零初始化形状（a，b）的矩阵。

def initialize_parameters(n_x,n_h,n_y):
    np.random.seed(2)

    W1=np.random.randn(n_h,n_x)
    b1=np.zeros((n_h,1))
    W2=np.random.randn(n_y,n_h)
    b2=np.zeros((n_y,1))

    assert (W1.shape == (n_h, n_x))
    assert (b1.shape == (n_h, 1))
    assert (W2.shape == (n_y, n_h))
    assert (b2.shape == (n_y, 1))

    parameters={"W1":W1,
    "b1":b1,
    "W2":W2,
    "b2":b2}

    return parameters

n_x,n_h,n_y=initialize_parameters_test_case()
parameters = initialize_parameters(n_x, n_h, n_y)
print("W1 = " + str(parameters["W1"]))
print("b1 = " + str(parameters["b1"]))
print("W2 = " + str(parameters["W2"]))
print("b2 = " + str(parameters["b2"]))

4.3 - 循环

问题：实施forward_propagation()。

说明：
- 在上面查看分类器的数学表示。
- 您可以使用该功能sigmoid()。它内置（导入）在笔记本中。
- 您可以使用该功能np.tanh()。它是numpy lib的一部分。
- 您必须实现的步骤是：
1。使用，从字典“参数”（这是输出initialize_parameters()）中检索每个参数parameters[".."]。
2.实施正向传播。计算,和,（您对训练集中所有示例的所有预测的向量）。
- 反向传播所需的值存储在“ cache”中。cache将被给定为一个输入反向传播的函数。

def forward_propagation(X,parameters):
    W1=parameters["W1"]
    b1=parameters["b1"]
    W2=parameters["W2"]
    b2=parameters["b2"]

    Z1=np.dot(W1,X)+b1
    A1=np.tanh(Z1)
    Z2=np.dot(W2,A1)+b2
    A2=sigmoid(Z2)

    assert(A2.shape==(1,X.shape[1]))

    cache={"Z1":Z1,
    "A1":A1,
    "Z2":Z2,
    "A2":A2}

    return A2,cache 

X_assess,parameters=forward_propagation_test_case()
A2,cache=forward_propagation(X_assess,parameters)

print(np.mean(cache["Z1"]),np.mean(cache["A1"]),np.mean(cache["Z2"]),np.mean(cache["A2"]))

练习：实现compute_cost()计算成本J的值.

说明：

有许多方法可以实现cross-entropy loss。为了帮助您，我们将为您提供实施方式

（你可以使用np.multiply()，然后np.sum()或直接使用np.dot()）。

def compute_cost(A2,Y,parameters):
    m=Y.shape[1]

    logprobs=np.multiply(np.log(A2),Y)+np.multiply(np.log(1-A2),(1-Y))
    cost=-(1.0/m)*np.sum(logprobs)

    cost=np.squeeze(cost)

    assert(isinstance(cost,float))

    return cost

A2,Y_assess,parameters=compute_cost_test_case()
print("cost = " + str(compute_cost(A2, Y_assess, parameters)))

使用cache计算正向传播期间，您现在可以实现逆向传播。

问题：实现功能backward_propagation()。

说明：
逆向传播通常是深度学习中最难（最具数学性）的部分。为了帮助您，这里再次是关于反向传播的演讲的幻灯片。您将要使用此幻灯片右侧的六个等式，因为您正在构建向量化实现。

 

 

• 提示： 

为了计算dZ1你需要计算,当时tanh激活函数,如果,那么,所以,你可以用(1 - np.power(A1, 2))计算

def backward_propagation(parameters,cache,X,Y):
    m=X.shape[1]

    W1=parameters["W1"]
    W2=parameters["W2"]

    A1=cache["A1"]
    A2=cache["A2"]

    dZ2=A2-Y
    dW2=1.0/m*np.dot(dZ2,A1.T)
    db2=1.0/m*np.sum(dZ2,axis=1,keepdims=True)
    dZ1=np.dot(W2.T,dZ2)*(1-np.power(A1,2))
    dW1=1.0/m*np.dot(dZ1,X.T)
    db1=1.0/m*np.sum(dZ1,axis=1,keepdims=True)

    grads={"dW1":dW1,
    "db1":db1,
    "dW2":dW2,
    "db2":db2}

    return grads

parameters, cache, X_assess, Y_assess = backward_propagation_test_case()

grads = backward_propagation(parameters, cache, X_assess, Y_assess)
print ("dW1 = "+ str(grads["dW1"]))
print ("db1 = "+ str(grads["db1"]))
print ("dW2 = "+ str(grads["dW2"]))
print ("db2 = "+ str(grads["db2"]))

问题：实施更新规则。使用渐变下降。您必须使用（dW1，db1，dW2，db2）才能更新（W1，b1，W2，b2）。

一般梯度下降规则：,表示学习率,表示一个参数

def update_parameters(parameters,grads,learning_rate=1.2):
    W1=parameters["W1"]
    b1=parameters["b1"]
    W2=parameters["W2"]
    b2=parameters["b2"]

    dW1=grads["dW1"]
    db1=grads["db1"]
    dW2=grads["dW2"]
    db2=grads["db2"]

    W1=W1-learning_rate*dW1
    b1=b1-learning_rate*db1
    W2=W2-learning_rate*dW2
    b2=b2-learning_rate*db2

    parameters={"W1":W1,
    "b1":b1,
    "W2":W2,
    "b2":b2}

    return parameters

parameters, grads = update_parameters_test_case()
parameters = update_parameters(parameters, grads)

print("W1 = " + str(parameters["W1"]))
print("b1 = " + str(parameters["b1"]))
print("W2 = " + str(parameters["W2"]))
print("b2 = " + str(parameters["b2"]))

4.4 - 在nn_model（）中集成部件4.1,4.2和4.3

问题：构建你的神经网络模型nn_model()。

说明：神经网络模型必须按正确的顺序使用以前的功能。

4.5预测

问题：使用模型通过构建predict（）进行预测。
使用前向传播来预测结果。

提醒:预测=

例如，如果您想根据阈值将矩阵X的条目设置为0和1，您将执行以下操作： X_new = (X > threshold)

def predict(parameters,X):
    A2,cache=forward_propagation(X,parameters)
    predictions=(A2>0.5)
    
    return predictions

parameters, X_assess = predict_test_case()
predictions = predict(parameters, X_assess)
print("predictions mean = " + str(np.mean(predictions)))

是时候运行模型并查看它在平面数据集上的表现。运行以下代码以使用n的单个隐藏层测试模型HñH隐藏的单位。

X,Y=load_planar_dataset()

# Build a model with a n_h-dimensional hidden layer
parameters = nn_model(X, Y, n_h = 4, num_iterations = 10000, print_cost=True)

# Plot the decision boundary
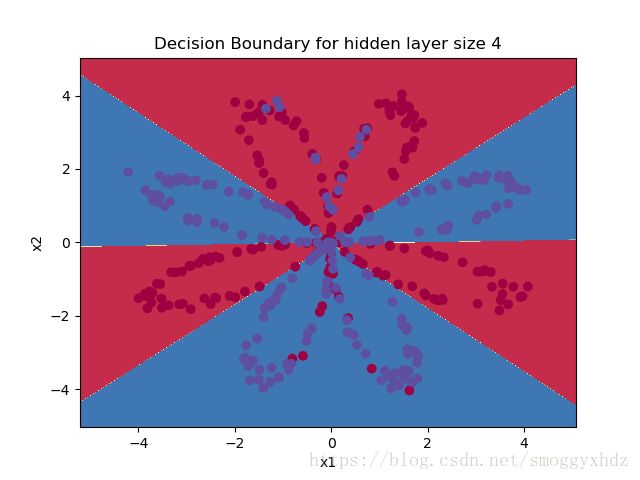
plot_decision_boundary(lambda x: predict(parameters, x.T), X, Y.flatten())
plt.title("Decision Boundary for hidden layer size " + str(4))
plt.show()

predictions = predict(parameters, X)
print ('Accuracy: %d' % float((np.dot(Y,predictions.T) + np.dot(1-Y,1-predictions.T))/float(Y.size)*100) + '%')

与Logistic回归相比，准确度非常高。该模型已经了解了花的叶子图案！与逻辑回归不同，神经网络能够学习甚至高度非线性的决策边界。

现在，让我们试试几个隐藏的图层大小。

4.6 - 调整隐藏层大小（可选/未分级练习）

运行以下代码。可能需要1-2分钟。您将观察模型对各种隐藏图层大小的不同行为。

X,Y=load_planar_dataset()

plt.figure(figsize=(16, 32))
hidden_layer_sizes = [1, 2, 3, 4, 5, 20, 50]
for i, n_h in enumerate(hidden_layer_sizes):
    plt.subplot(5, 2, i+1)
    plt.title('Hidden Layer of size %d' % n_h)
    parameters = nn_model(X, Y, n_h, num_iterations = 5000)
    plot_decision_boundary(lambda x: predict(parameters, x.T), X, Y.flatten())
    predictions = predict(parameters, X)
    accuracy = float((np.dot(Y,predictions.T) + np.dot(1-Y,1-predictions.T))/float(Y.size)*100)
    print ("Accuracy for {} hidden units: {} %".format(n_h, accuracy))

plt.show()

解释：
- 较大的模型（具有更多隐藏单位）能够更好地适应训练集，直到最终最大的模型过度拟合数据。 
- 最好的隐藏层大小似乎在n_h = 5左右。实际上，这里的值似乎很好地适合数据而不会引起明显的过度拟合。
- 您稍后还将学习正则化，它允许您使用非常大的模型（例如n_h = 50）而不会过度拟合。

您已经学会： 
- 构建一个隐藏层的完整神经网络
- 充分利用非线性单元
- 实现前向传播和反向传播，并训练神经网络
- 查看改变隐藏层大小的影响，包括过度拟合。