嘻嘻哈哈yjy
嘻嘻哈哈yjy

计算机视觉面试考点（18）边缘检测算子（Roberts、Prewitt、Sobel、Laplacian、LoG、Canny）

计算机视觉工程师在面试过程中主要考察三个内容：图像处理、机器学习、深度学习。然而，各类资料纷繁复杂，或是简单的知识点罗列，或是有着详细数学推导令人望而生畏的大部头。为了督促自己学习，也为了方便后人，决心将常考必会的知识点以通俗易懂的方式设立专栏进行讲解，努力做到长期更新。此专栏不求甚解，只追求应付一般面试。希望该专栏羽翼渐丰之日，可以为大家免去寻找资料的劳累。每篇介绍一个知识点，没有先后顺序。想了解什么知识点可以私信或者评论，如果重要而且恰巧我也能学会，会尽快更新。最后，每一个知识点我会参考很多资料。考虑到简洁性，就不引用了。如有冒犯之处，联系我进行删除或者补加引用。在此先提前致歉了！

边缘检测算子是用来提取图形边缘的卷积核

边缘提取原理
边缘处的像素值通常会有明显变化
衡量连续的变化可以使用导数
衡量图像像素间离散的变化使用差分
导数：(f(x+Δx)-f(x))/Δx
差分：f(x+1)-f(x)

梯度表示
梯度表示包含大小和方向

如果只有一个算子
只能表示大小

如果有两个算子
两个算子计算的梯度的方向是互相垂直的
如果计算的大小分别为Gx和Gy
方向为：
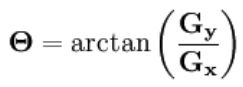
在这里插入图片描述
大小有三种：
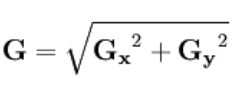
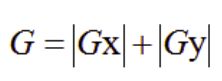
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述

Roberts

计算机视觉面试考点（18）边缘检测算子（Roberts、Prewitt、Sobel、Laplacian、LoG、Canny）_第1张图片
很直观，我们会想到分别计算x方向和y方向的差分
于是我们得到两个算子
[-1 1]
和
[-1
1]
但是我们可以发现它们计算的区域不同，只有一个点重合
所以升级为
[-1 1
-1 1]
和
[-1 -1
1 1]
考虑到三个因素：

  1. 计算量
  2. 实验效果
  3. 像素间距离很小，计算对角差分和相邻的差分，实际意义相差不大（这点事个人理解）

于是最后产生了Roberts算子

Prewitt

计算机视觉面试考点（18）边缘检测算子（Roberts、Prewitt、Sobel、Laplacian、LoG、Canny）_第2张图片
以第一个算子为例
想计算中心点x方向的梯度
额外考虑了上一行和下一行x方向的梯度
相当于取了平均

Sobel

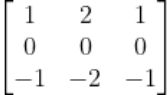
在这里插入图片描述
在这里插入图片描述
在Prewitt取平均的基础上
对当前行（列）增加了权重
相当于加权平均
实验证明，这样效果好一些

变种：
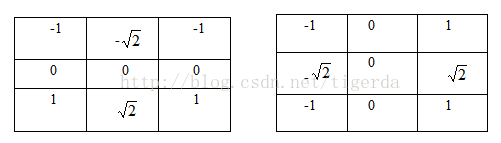
计算机视觉面试考点（18）边缘检测算子（Roberts、Prewitt、Sobel、Laplacian、LoG、Canny）_第3张图片
这个的加权平均就严格按照距离的比例关系来了
因为对角的距离是相邻距离的根号2倍

Laplacian

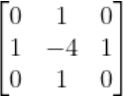
在这里插入图片描述
以上都是一阶差分
Laplacian是二阶差分
证明：
仅考虑x方向
一阶：
中心点右边的点：f(x+1)-f(x)
中心点左边的点：f(x)-f(x-1)
二阶：
中心点：
[f(x+1)-f(x)]-[f(x)-f(x-1)]=f(x+1)+f(x-1)-2f(x)
再考虑到y方向，相加即可得到Laplacian

扩展模式：
在这里插入图片描述

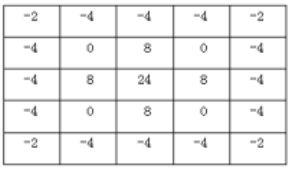
LoG(Laplacian of Gaussian)

原理
高斯平滑（模糊）和拉普拉斯结合

这个模板就不固定了
大小不再局限于3x3
通常可以是5x5
根据方差不同
模板中的数值也不同

主要目的
高斯平滑可以去噪

该算子的一个例子(下文会介绍推导)
计算机视觉面试考点（18）边缘检测算子（Roberts、Prewitt、Sobel、Laplacian、LoG、Canny）_第4张图片

Canny

Canny严格来说应该是一种算法

步骤：
1.RGB变灰度图（其它算子也都是计算灰度图，没有太大必要计算三通道再取平均，毕竟计算的是边缘信息，颜色信息不重要）
2.高斯平滑去噪
3.使用任意算子计算梯度大小和方向（因为要计算大小和方向，所以Laplacian等相关算子就不能用了）
4.非极大值抑制
将梯度方向分为4部分（因为向上和向下对于梯度没影响，所以把360度转换为180度）
计算机视觉面试考点（18）边缘检测算子（Roberts、Prewitt、Sobel、Laplacian、LoG、Canny）_第5张图片
计算机视觉面试考点（18）边缘检测算子（Roberts、Prewitt、Sobel、Laplacian、LoG、Canny）_第6张图片
比如现在2行3列的7是中心点
它的方向是上下走向
找到上下方向的相邻点4和5
因为7比4和5大
所以7保留

注意：
一定是该方向上相邻的两个点
比如方向为右上
那么相邻的点就是右上角和左下角

5.双阈值边缘连接
设定两个阈值high和low
梯度大小大于high的保留
梯度大小小于low的去除（梯度大小修改为0）
梯度在low和high之间的做8邻域连接
如果8邻域内有大于high的，那么该中心点保留，否则去除

8邻域就是中心点周围的8个点

关于高斯

噪声通常是像素值突变的点

举个例子
在5x5的范围内，将所有像素值平均
可以减小这种突变
实现了去噪

这样的坏处是，图像的信息也没了

为了缓解上述情况
我们想到增加中心点的权重
离中心点距离越远，权重越小
高斯分布满足这一条件

所以高斯平滑算子可以用以下公式得到
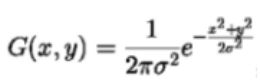
在这里插入图片描述
进一步
LoG是高斯和拉普拉斯的结合
拉普拉斯是二阶差分
所以我们对上式关于x和y分别求二阶导并相加
得到
计算机视觉面试考点（18）边缘检测算子（Roberts、Prewitt、Sobel、Laplacian、LoG、Canny）_第7张图片
比如中心点是（3,3）
那么LoG算子（4,5）处的值就是把x=1,y=2代入上式

还有个超参数是高斯函数的方差
方差越大，高斯函数越平缓，去噪效果越好，图像越模糊

优缺点分析
优缺点没那么绝对，也很难死记硬背，还是要学会分析

上文提到，平均可以去噪
那么有平均思想的算子就对噪声不敏感
比如Prewitt、Sobel
有了平均思想自然会造成一定的信息模糊
所以边缘定位会因此效果下降
Roberts没有这种平均思想
在噪声小的条件下，边缘定位就会准确一些

一阶差分形容像素值变化趋势
二阶差分形容变化趋势的快慢或者说剧烈程度
显然噪声的变化程度剧烈
那么没有去噪处理的Laplacian对噪声就会敏感

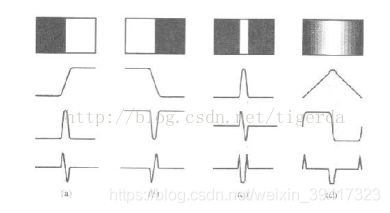
计算机视觉面试考点（18）边缘检测算子（Roberts、Prewitt、Sobel、Laplacian、LoG、Canny）_第8张图片
四行分别是
常见边缘
像素变化
一阶差分
二阶差分

因为梯度大小要取绝对值或者平方
所以应该将小于0的部分向上翻转

可以看出
二阶差分算子容易检测出双边缘
一阶算子比较适合灰度渐变

Canny这种有很多步骤的就可以根据步骤分析
高斯平滑：去噪
双阈值连接：连接一些弱边缘
Canny更像一个集大成者
毕竟它已经上升到算法层面了

我觉得学会分析这些就够了，优缺点还是挺难记的

完
欢迎讨论 欢迎吐槽

你可能感兴趣的:(计算机视觉面试考点,计算机视觉,面试,边缘检测,算子,Canny)

  • 家长们的福音：教师对书面作业全批全改，学校不得考试选拔学生 丝雨润春风
    年前年后教育部门公布了不少措施，来减轻学生负担，维护学生的身心健康成长，随后各地教育局也陆陆续续颁布了各种新政策，这不最近山东教育厅也起草了《山东普通中小学规范办学十五条规定》。在这15条规定内容之中包括了：教师对书面作业全批全改，不给家长布置作业或要求家长评改作业；义务教育学校不得以考试、面试、评测等名义选拔学生；保障学生每天睡眠时间，高中生不少于8个小时。毋庸置疑这个规定的初衷非常得好，是对学
  • 2.5 项目讲解流程 王守谦26 项目资料数据库
    一、项目讲解1、自我介绍2、项目流程-===============================二、自我介绍（一）、学员自我介绍，讲解存在的问题比如：讲解年份、卡顿、重点学历、忘记（二）自我规则内容1、开场白：礼貌用语2、时间：自我介绍1-2分钟以内3、内容：姓名、籍贯、毕业院校、（拉进面试官距离）4、技能：功能测试、接口测试、自动化测试、app测试、性能测试、安全测试黑盒测试、白盒测试、灰盒
  • MyBatis高级面试题-2024 my_styles mybatisjava开发语言面试题
    MyBatis的核心组件有哪些？首先第一个是，SqlSessionFactory，它就像是一个会话工厂。它的任务是创建SqlSession对象，这个对象是我们与数据库交互的主要途径。SqlSessionFactory的作用很重要，因为它可以帮我们配置数据库连接信息和事务管理等。一旦这个工厂被建立起来，它就会加载一些必要的配置和映射文件，为后续的数据库操作提供一个可靠的基础。第二个是SqlSessi
  • 排序算法太多？常用排序都在这了，一篇文章总结和实现所有面试会考的排序算法（基于Python实现） 宇宙之一粟 不归路之Python#IT面试题收集与总结数据结构与算法算法数据结构排序算法pythonjava
    文章目录排序算法1.常见的排序算法1.1选择排序1.1.1思想1.1.2实现**1.1.3选择排序分析**1.2冒泡排序**1.2.1思想****1.2.2实现****1.2.3冒泡排序分析**1.3插入排序**1.3.1思想****1.3.2实现****1.3.3插入排序分析**1.4归并排序☆☆★**1.4.1思想****1.4.2实现****1.4.3归并排序分析**1.5快速排序☆★★**
  • 风险管理和采购管理核心考点梳理 WorkLee PMPPMP风险管理采购管理
    个人总结，仅供参考，欢迎加好友一起讨论PMP-风险管理和采购管理核心考点梳理风险管理风险是一个中性词，包括机会和威胁。风险管理的子过程非常多，但是相对来说子过程之间的逻辑非常清晰，整个风险管理的过程都是在维护一个非常重要的工件-风险登记册。风险管理是项目管理全生命周期都要开展的。1）规划风险管理风险管理计划包含哪些内容？解析：风险管理计划是描述如何安排与实施风险管理活动。（风险管理计划中无风险）包
  • 沟通管理和相关方管理核心考点梳理 WorkLee PMPPMP沟通管理相关方干系人
    个人总结，仅供参考，欢迎加好友一起讨论PMP-沟通管理和相关方管理核心考点梳理沟通管理和相关方（干系人）管理这两章放在一起进行梳理，这两章很多的考点很容易混淆，经常会纠结于一些题目，究竟选择沟通管理还是干系人管理的知识点。沟通管理1）规划沟通管理沟通在PMP中是指信息流的传递，PM是根据谁的需求来确定这种信息流的传递方式、频率，内容、格式呢？解析：规划沟通管理是基于每个相关方或相关方群体的信息需求
  • 15：00面试，15：06就出来了，问的问题有点变态。。。 爱学习的执念 面试软件测试软件测试面试面试职场和发展
    从小厂出来，没想到在另一家公司又寄了。到这家公司开始上班，加班是每天必不可少的，看在钱给的比较多的份上，就不太计较了。没想到9月一纸通知，所有人不准加班，加班费不仅没有了，薪资还要降40%,这下搞的饭都吃不起了。还在有个朋友内推我去了一家互联网公司，兴冲冲见面试官，没想到一道题把我给问死了：如果模块请求http改为了https,测试方案应该如何制定，修改?感觉好简单的题，硬是没有答出来，早知道好好
  • 工资高压力大工资低休息多你怎么选择 绿蘋果
    人总是面临很多选择，不久前自己刚刚放弃一份薪水还不错的工作，为了能多点时间陪陪孩子，也适当的让自己放松放松，运气好，离职后赶上疫情，对于没有人依赖的我，瞬间压力好大，本来是准备休息陪陪孩子出去走走的，这门还没出呢，就不能出门了。我承认自己有些心慌了，需要赶紧找工作了，在家休息一个月不到，我又开始赶急赶忙的找工作，一年已经过半，开始找只能网上投投简历，一直也没回复，后边终于收到面试电话了，对于来之不
  • Vue 常见面试题(一) 安生生申 面试题vue.js前端javascript
    目录1、Vue的最大的优势是什么？（必会）2、Vue和jQuery两者之间的区别是什么？（必会）3、MVVM和MVC区别是什么？哪些场景适合？（必会）1、基本定义2、使用场景3、两者之间的区别4、Vue数据双向绑定的原理是什么?（必会）5、Object.defineProperty和Proxy的区别（必会）6、Vue生命周期总共分为几个阶段？（必会）7、第一次加载页面会触发哪几个钩子函数？（必会）
  • Java回溯知识点（含面试大厂题和源码） 一成码农 java面试开发语言
    回溯算法是一种通过遍历所有可能的候选解来寻找所有解的算法，如果候选解被确认不是一个解（或至少不是最后一个解），回溯算法会通过在上一步进行一些变化来丢弃这个解，即“回溯”并尝试另一个候选解。回溯法通常用递归方法来实现，在解决排列、组合、选择问题时非常有效。回溯算法的核心要点：路径：也就是已经做出的选择。选择列表：也就是你当前可以做的选择。结束条件：也就是到达决策树底层，无法再做出选择的条件。回溯算法
  • java基础相关面试题详细总结 。。。。。96 java开发语言
    1.Java中的数据类型有哪些？答：Java中的数据类型包括基本数据类型（如整数、浮点数、字符等）和引用数据类型（如类、接口、数组等）。2.什么是面向对象编程（OOP）？答：面向对象编程是一种编程范式，它将数据和对数据的操作封装在一起，形成对象。通过对象之间的交互来实现程序的功能。3.解释类和对象的关系。答：类是对象的抽象描述，而对象是类的具体实例。一个类可以创建多个对象，每个对象都具有类中定义的
  • Java面试题：解释JVM的内存结构，并描述堆、栈、方法区在内存结构中的角色和作用，Java中的多线程是如何实现的，Java垃圾回收机制的基本原理，并讨论常见的垃圾回收算法 杰哥在此 Java系列javajvm算法面试
    Java内存模型与多线程的深入探讨在Java的世界里，内存模型和多线程是开发者必须掌握的核心知识点。它们不仅关系到程序的性能和稳定性，还直接影响到系统的可扩展性和可靠性。下面，我将通过三个面试题，带领大家深入理解Java内存模型、多线程以及并发编程的相关原理和实践。面试题一：请解释JVM的内存结构，并描述堆、栈、方法区在内存结构中的角色和作用。关注点：JVM内存结构的基本组成堆、栈、方法区的功能和
  • OpenCV（一个C++人工智能领域重要开源基础库） 简介 愚梦者 OpenCV人工智能人工智能opencvc++图像处理计算机视觉开源
    返回：OpenCV系列文章目录（持续更新中......）上一篇：OpenCV4.9.0配置选项参考下一篇：OpenCV4.9.0开源计算机视觉库安装概述引言：OpenCV（全称OpenSourceComputerVisionLibrary）是一个基于开放源代码发行的跨平台计算机视觉库，可以用来进行图像处理、计算机视觉和机器学习等领域的开发。该库由英特尔公司于1999年开始开发，最初是为了加速处理器
  • Flink算子通用状态应用测试样例 公子乂 flinkjavaservlet
    Flink算子通用状态应用测试样例1.获取Flink执行环境finalStreamExecutionEnvironmentenv=StreamExecutionEnvironment.getExecutionEnvironment();env.setParallelism(1);2.创建数据源，生成随机数据DataStream>source=env.addSource(newSourceFunct
  • C++面试题 虾仁A 面试c++
    目录一、堆和栈的区别二、C++中new、delte和malloc的区别三、什么是源对象四、C++有哪些设计模式五，你使用过C++哪些类型的指针一、堆和栈的区别特性堆栈申请方式由程序员显式申请和释放由系统自动分配和释放分配方式动态分配自动分配分配效率相对较慢，需要遍历内存链表寻找合适空间相对较快，系统直接分配内存地址不连续的内存区域连续的内存区域大小限制大小灵活，上限取决于虚拟内存大小固定，通常较小
  • 15：00面试，15：06就出来了，问的问题有点变态。。。 程序员油条 自动化测试软件测试面试面试职场和发展
    从小厂出来，没想到在另一家公司又寄了。到这家公司开始上班，加班是每天必不可少的，看在钱给的比较多的份上，就不太计较了。没想到9月一纸通知，所有人不准加班，加班费不仅没有了，薪资还要降40%,这下搞的饭都吃不起了。还在有个朋友内推我去了一家互联网公司，兴冲冲见面试官，没想到一道题把我给问死了：如果模块请求http改为了https,测试方案应该如何制定，修改?感觉好简单的题，硬是没有答出来，早知道好好
  • 16：00面试，16：06就出来了，问的问题有点变态。。。 咖啡加剁椒⑨ 软件测试自动化测试软件测试功能测试程序人生职场和发展面试
    从小厂出来，没想到在另一家公司又寄了。到这家公司开始上班，加班是每天必不可少的，看在钱给的比较多的份上，就不太计较了。没想到8月一纸通知，所有人不准加班，加班费不仅没有了，薪资还要降40%,这下搞的饭都吃不起了。还在有个朋友内推我去了一家互联网公司，兴冲冲见面试官，没想到一道题把我给问死了：如果模块请求http改为了https,测试方案应该如何制定，修改?感觉好简单的题，硬是没有答出来，早知道好好
  • 9：00面试，9：06就出来了，问的问题有点变态。。。 咖啡加剁椒⑦ 软件测试面试职场和发展功能测试软件测试自动化测试程序人生
    从小厂出来，没想到在另一家公司又寄了。到这家公司开始上班，加班是每天必不可少的，看在钱给的比较多的份上，就不太计较了。没想到8月一纸通知，所有人不准加班，加班费不仅没有了，薪资还要降40%,这下搞的饭都吃不起了。还在有个朋友内推我去了一家互联网公司，兴冲冲见面试官，没想到一道题把我给问死了：如果模块请求http改为了https,测试方案应该如何制定，修改?感觉好简单的题，硬是没有答出来，早知道好好
  • 关于HDP的20道高级运维面试题 编织幻境的妖 运维
    1.描述HDP的主要组件及其作用。HDP（HortonworksDataPlatform）的主要组件包括Hadoop框架、HDFS、MapReduce、YARN以及Hadoop生态系统中的其他关键工具，如Spark、Flink、Hive、HBase等。以下是对这些组件及其作用的具体描述：Hadoop框架:Hadoop是一个开源的分布式计算框架，用Java语言编写，用于存储和处理大规模数据集。它广义
  • MyBatis面试专题 XMYX-0 面试mybatis面试职场和发展
    文章目录什么是MyBatis？讲下MyBatis的缓存一级缓存二级缓存Mybatis是如何进行分页的？分页插件的原理是什么？分页插件的原理举例说明简述Mybatis的插件运行原理，以及如何编写一个插件？插件运行原理编写一个插件的基本步骤Mybatis动态sql是做什么的？都有哪些动态sql？能简述一下动态sql的执行原理不？动态SQL的执行原理#{}和${}的区别是什么？为什么说Mybatis是半
  • 【笔试】银行校招，信息科技岗 & 金融科技岗笔试准备方向 小哈里 就业科技金融春招笔试银行
    【笔试】银行校招，信息科技&金融科技岗笔试准备方向文章目录1、银行招聘流程（投递）2、笔试内容分析（笔试）3、真题题库（BOC）3.1职业能力（行测）3.2英语3.3信息科技1、银行招聘流程（投递）一般银行面试流程分为以下几步：网上提交简历（内容非常多，没有PDF，全部表单）笔试（全国统一，线下考点）一面（偏技术面）二面（无领导面试、半结构化面试）体检签约会简历：通常银行的要填写的简历内容非常多，
  • MyBatis面试简答题 糯米小麻花啊 mybatis
    以下是一份MyBatis的高难度简答题，共20题：请解释MyBatis中#{}和${}的区别，并举例说明它们在实际应用中的使用场景。MyBatis的Mapper接口是如何与XML映射文件关联的？如何在MyBatis中实现动态SQL？请列举几种常见的动态SQL元素并解释其作用。描述MyBatis中的ResultMap的作用，并说明如何定义和使用它。MyBatis如何处理数据库中的null值？请解释M
  • 想象与现实 西北到东南
    自打那一天开始，我就意识到，想象与现实之间的鸿沟几乎要无法填补了。再来意识到，想要从事一件自己所喜爱的事情是多么难能可贵，且过于理想的事情。记得是上个月，我准备实习，在几经寻找与数次努力后。我成功的进入了一家报社实习，应聘的岗位是文字编辑。在面试时，我将自己部分所写文章交给那两位领导阅后，领导对此表示认可，认为我可以胜任这份工作。但事与愿违，当我满怀欣喜的工作后，却发现每天的内容居然是与设计所相关
  • 苏舜钦惨遭贬谪，途中写下一首绝美小诗，读懂之后令人感慨万千 慢慢趣说
    无数个深夜醒来，浮现在你脑海中的往往都是些什么事情呢？曾经，你受到了委屈而被迫咽下的泪水，或者你因为某次重要考试发挥失常而不及格的悔恨，亦或者在面试时一不小心就脱口而出的肤浅……人生在世，总有一些事和一些人，让你彻夜难眠，久久无法忘怀。其中，遭遇贬谪，对古代很多读书人来说，都无异于人生的晴天霹雳，许多人的一生也会因此发生重大改变。然而，对宋代著名词人苏舜钦来说，无论处于什么情况下，调整好自己的心态
  • 10：00面试，10：06就出来了，问的问题有点变态。。。 咖啡加剁椒⑧ 软件测试面试职场和发展软件测试自动化测试功能测试程序人生
    从小厂出来，没想到在另一家公司又寄了。到这家公司开始上班，加班是每天必不可少的，看在钱给的比较多的份上，就不太计较了。没想到8月一纸通知，所有人不准加班，加班费不仅没有了，薪资还要降40%,这下搞的饭都吃不起了。还在有个朋友内推我去了一家互联网公司，兴冲冲见面试官，没想到一道题把我给问死了：如果模块请求http改为了https,测试方案应该如何制定，修改?感觉好简单的题，硬是没有答出来，早知道好好
  • 4、再一次面试 小猪和懒懒
    五年后老方喊阿溪去办公室，说有事交代。“你被推荐到总部参加后备干部选拔，需要准备一些材料，还有面试”。“你考试和面试肯定都是没问题的，但是之前有推荐的人面试没有通过，大老板亲自定的你”。阿溪有点意外，但也在预料之中，五年了，跟着公司风风雨雨，自己是有这个资格的。但是，内部还要考试、面试，而且之前还有人没有通过，这应该不只是走走过场，阿溪也没把握。进公司五年，阿溪一直做招聘工作，面试的人没有上万肯定
  • 面试九 设计模式 余生有烟火 面试职场和发展c++linux设计模式
    单例模式通常被归类为创建型设计模式，因为它主要关注如何创建对象的实例，以及如何确保在整个应用程序生命周期中只有一个实例存在。1.为什么日志模块和数据库连接池需要单例模式使用单例模式来实现数据库连接池主要有以下几个原因：全局唯一性：数据库连接池在应用程序中通常是一个全局资源，多个部分都需要共享同一个连接池。使用单例模式可以确保整个应用程序中只存在一个数据库连接池的实例，避免了资源浪费和连接冲突。统一
  • 神经网络（深度学习，计算机视觉，得分函数，损失函数，前向传播，反向传播，激活函数） MarkHD 深度学习神经网络计算机视觉
    神经网络，特别是深度学习，在计算机视觉等领域有着广泛的应用。以下是关于你提到的几个关键概念的详细解释：神经网络：神经网络是一种模拟人脑神经元结构的计算模型，用于处理复杂的数据和模式识别任务。它由多个神经元（或称为节点）组成，这些神经元通过权重和偏置进行连接，并可以学习调整这些参数以优化性能。深度学习：深度学习是神经网络的一个子领域，主要关注于构建和训练深度神经网络（即具有多个隐藏层的神经网络）。通
  • 比较好的知识点 hc.Geng java
    2023年Java超全面试题及答案解析---https://blog.csdn.net/qq_42301302/article/details/1287852747分钟带你细致解析4个Java算法必刷题---https://blog.csdn.net/hcxy2022/article/details/12796379750道JAVA基础算法编程题【内含分析、程序答案】---https://blog
  • 什么是特征检测和描述，OpenCV中常见的特征检测算法有哪些？ -Max-静- #opencv学习opencv算法人工智能
    特征检测和描述是计算机视觉中的基本概念，它们在图像识别、对象跟踪、图像拼接等多种任务中发挥着至关重要的作用。特征检测是指识别图像中重要的特定点、区域或结构，这些特征通常具有独特性、可重复性以及对光照变化、旋转和比例变换等变化的鲁棒性。这些特征点可以用作进一步分析的参考。特征描述是基于一定的几何或者颜色信息生成特征点的特征描述符，这种描述应满足欧式空间的仿射不变性和噪声鲁棒性，并且不同特征点的特征描
  • PHP，安卓，UI，java，linux视频教程合集 cocos2d-x小菜 javaUIPHPandroidlinux
    ╔-----------------------------------╗┆                           
  • 各表中的列名必须唯一。在表 'dbo.XXX' 中多次指定了列名 'XXX'。 bozch .net.net mvc
    在.net mvc5中，在执行某一操作的时候，出现了如下错误：       各表中的列名必须唯一。在表 'dbo.XXX' 中多次指定了列名 'XXX'。 经查询当前的操作与错误内容无关，经过对错误信息的排查发现，事故出现在数据库迁移上。 回想过去： 在迁移之前已经对数据库进行了添加字段操作，再次进行迁移插入XXX字段的时候，就会提示如上错误。  &
  • Java 对象大小的计算 e200702084 java
                              Java对象的大小 如何计算一个对象的大小呢？    
  • Mybatis Spring 171815164 mybatis
    ApplicationContext ac = new ClassPathXmlApplicationContext("applicationContext.xml"); CustomerService userService = (CustomerService) ac.getBean("customerService"); Customer cust
  • JVM 不稳定参数 g21121 jvm
            -XX 参数被称为不稳定参数，之所以这么叫是因为此类参数的设置很容易引起JVM 性能上的差异，使JVM 存在极大的不稳定性。当然这是在非合理设置的前提下，如果此类参数设置合理讲大大提高JVM 的性能及稳定性。        可以说“不稳定参数”
  • 用户自动登录网站 永夜-极光 用户
    1.目标:实现用户登录后,再次登录就自动登录,无需用户名和密码 2.思路:将用户的信息保存为cookie            每次用户访问网站,通过filter拦截所有请求,在filter中读取所有的cookie,如果找到了保存登录信息的cookie,那么在cookie中读取登录信息,然后直接
  • centos7 安装后失去win7的引导记录 程序员是怎么炼成的 操作系统
    1.使用root身份(必须)打开 /boot/grub2/grub.cfg 2.找到 ### BEGIN /etc/grub.d/30_os-prober ###   在后面添加    menuentry "Windows 7 (loader) (on /dev/sda1)" { 
  • Oracle 10g 官方中文安装帮助文档以及Oracle官方中文教程文档下载 aijuans oracle
    Oracle 10g 官方中文安装帮助文档下载：http://download.csdn.net/tag/Oracle%E4%B8%AD%E6%96%87API%EF%BC%8COracle%E4%B8%AD%E6%96%87%E6%96%87%E6%A1%A3%EF%BC%8Coracle%E5%AD%A6%E4%B9%A0%E6%96%87%E6%A1%A3 Oracle 10g 官方中文教程
  • JavaEE开源快速开发平台G4Studio_V3.2发布了 無為子 AOPoraclemysqljavaeeG4Studio
      我非常高兴地宣布,今天我们最新的JavaEE开源快速开发平台G4Studio_V3.2版本已经正式发布。大家可以通过如下地址下载。   访问G4Studio网站 http://www.g4it.org   G4Studio_V3.2版本变更日志 功能新增 (1).新增了系统右下角滑出提示窗口功能。 (2).新增了文件资源的Zip压缩和解压缩
  • Oracle常用的单行函数应用技巧总结 百合不是茶 日期函数转换函数(核心)数字函数通用函数(核心)字符函数
    单行函数;   字符函数,数字函数,日期函数,转换函数(核心),通用函数(核心) 一:字符函数: .UPPER(字符串) 将字符串转为大写 .LOWER (字符串) 将字符串转为小写 .INITCAP(字符串) 将首字母大写 .LENGTH (字符串) 字符串的长度 .REPLACE(字符串,'A','_') 将字符串字符A转换成_
  • Mockito异常测试实例 bijian1013 java单元测试mockito
    Mockito异常测试实例： package com.bijian.study; import static org.mockito.Mockito.mock; import static org.mockito.Mockito.when; import org.junit.Assert; import org.junit.Test; import org.mockito.
  • GA与量子恒道统计 Bill_chen JavaScript浏览器百度Google防火墙
    前一阵子，统计**网址时，Google Analytics（GA） 和量子恒道统计（也称量子统计），数据有较大的偏差，仔细找相关资料研究了下，总结如下：   为何GA和量子网站统计（量子统计前身为雅虎统计）结果不同？ 首先：没有一种网站统计工具能保证百分之百的准确出现该问题可能有以下几个原因：（1）不同的统计分析系统的算法机制不同；（2）统计代码放置的位置和前后
  • 【Linux命令三】Top命令 bit1129 linux命令
    Linux的Top命令类似于Windows的任务管理器，可以查看当前系统的运行情况，包括CPU、内存的使用情况等。如下是一个Top命令的执行结果：     top - 21:22:04 up 1 day, 23:49, 1 user, load average: 1.10, 1.66, 1.99 Tasks: 202 total, 4 running, 198 sl
  • spring四种依赖注入方式 白糖_ spring
      平常的java开发中，程序员在某个类中需要依赖其它类的方法，则通常是new一个依赖类再调用类实例的方法，这种开发存在的问题是new的类实例不好统一管理，spring提出了依赖注入的思想，即依赖类不由程序员实例化，而是通过spring容器帮我们new指定实例并且将实例注入到需要该对象的类中。依赖注入的另一种说法是“控制反转”，通俗的理解是：平常我们new一个实例，这个实例的控制权是我
  • angular.injector boyitech AngularJSAngularJS API
    angular.injector   描述: 创建一个injector对象, 调用injector对象的方法可以获得angular的service, 或者用来做依赖注入.   使用方法: angular.injector(modules, [strictDi])   参数详解: Param Type Details mod
  • java-同步访问一个数组Integer[10]，生产者不断地往数组放入整数1000，数组满时等待；消费者不断地将数组里面的数置零，数组空时等待 bylijinnan Integer
    public class PC { /** * 题目：生产者-消费者。 * 同步访问一个数组Integer[10]，生产者不断地往数组放入整数1000，数组满时等待；消费者不断地将数组里面的数置零，数组空时等待。 */ private static final Integer[] val=new Integer[10]; private static
  • 使用Struts2.2.1配置 Chen.H apachespringWebxmlstruts
    Struts2.2.1 需要如下 jar包: commons-fileupload-1.2.1.jar commons-io-1.3.2.jar commons-logging-1.0.4.jar freemarker-2.3.16.jar javassist-3.7.ga.jar ognl-3.0.jar spring.jar struts2-core-2.2.1.jar struts2-sp
  • [职业与教育]青春之歌 comsci 教育
           每个人都有自己的青春之歌............但是我要说的却不是青春...        大家如果在自己的职业生涯没有给自己以后创业留一点点机会,仅仅凭学历和人脉关系,是难以在竞争激烈的市场中生存下去的....   &nbs
  • oracle连接(join)中使用using关键字 daizj JOINoraclesqlusing
    在oracle连接(join)中使用using关键字 34. View the Exhibit and examine the structure of the ORDERS and ORDER_ITEMS tables. Evaluate the following SQL statement: SELECT oi.order_id, product_id, order_date FRO
  • NIO示例 daysinsun nio
    NIO服务端代码： public class NIOServer { private Selector selector; public void startServer(int port) throws IOException { ServerSocketChannel serverChannel = ServerSocketChannel.open(
  • C语言学习homework1 dcj3sjt126com chomework
    0、 课堂练习做完 1、使用sizeof计算出你所知道的所有的类型占用的空间。 int x; sizeof(x);   sizeof(int);   # include <stdio.h> int main(void) { int x1; char x2; double x3; float x4; printf(&quo
  • select in order by , mysql排序 dcj3sjt126com mysql
    If i select like this: SELECT id FROM users WHERE id IN(3,4,8,1); This by default will select users in this order 1,3,4,8, I would like to select them in the same order that i put IN() values so:
  • 页面校验-新建项目 fanxiaolong 页面校验
    $(document).ready( function() { var flag = true; $('#changeform').submit(function() { var projectScValNull = true; var s =""; var parent_id = $("#parent_id").v
  • Ehcache（02）——ehcache.xml简介 234390216 ehcacheehcache.xml简介
    ehcache.xml简介          ehcache.xml文件是用来定义Ehcache的配置信息的，更准确的来说它是定义CacheManager的配置信息的。根据之前我们在《Ehcache简介》一文中对CacheManager的介绍我们知道一切Ehcache的应用都是从CacheManager开始的。在不指定配置信
  • junit 4.11中三个新功能 jackyrong java
    junit 4.11中两个新增的功能，首先是注解中可以参数化，比如 import static org.junit.Assert.assertEquals; import java.util.Arrays; import org.junit.Test; import org.junit.runner.RunWith; import org.junit.runn
  • 国外程序员爱用苹果Mac电脑的10大理由 php教程分享 windowsPHPunixMicrosoftperl
    Mac 在国外很受欢迎，尤其是在 设计/web开发/IT 人员圈子里。普通用户喜欢 Mac 可以理解，毕竟 Mac 设计美观，简单好用，没有病毒。那么为什么专业人士也对 Mac 情有独钟呢？从个人使用经验来看我想有下面几个原因： 1、Mac OS X 是基于 Unix 的 这一点太重要了，尤其是对开发人员，至少对于我来说很重要，这意味着Unix 下一堆好用的工具都可以随手捡到。如果你是个 wi
  • 位运算、异或的实际应用 wenjinglian 位运算
    一． 位操作基础，用一张表描述位操作符的应用规则并详细解释。       二． 常用位操作小技巧，有判断奇偶、交换两数、变换符号、求绝对值。       三． 位操作与空间压缩，针对筛素数进行空间压缩。    &n
  • weblogic部署项目出现的一些问题（持续补充中……） Everyday都不同 weblogic部署失败
    好吧，weblogic的问题确实……   问题一： org.springframework.beans.factory.BeanDefinitionStoreException: Failed to read candidate component class: URL [zip:E:/weblogic/user_projects/domains/base_domain/serve
  • tomcat7性能调优（01） toknowme tomcat7
        Tomcat优化： 1、最大连接数最大线程等设置 <Connector port="8082" protocol="HTTP/1.1"                useBodyEncodingForURI="t
  • PO VO DAO DTO BO TO概念与区别 xp9802 javaDAO设计模式bean领域模型
    O/R Mapping 是 Object Relational Mapping（对象关系映射）的缩写。通俗点讲，就是将对象与关系数据库绑定，用对象来表示关系数据。在O/R Mapping的世界里，有两个基本的也是重要的东东需要了解，即VO，PO。 它们的关系应该是相互独立的，一个VO可以只是PO的部分，也可以是多个PO构成，同样也可以等同于一个PO（指的是他们的属性）。这样，PO独立出来，数据持
按字母分类： ABCDEFGHIJKLMNOPQRSTUVWXYZ其他