上采样方法
搜上采样的文章,看到了这篇,虽然现在自己还用不太到,但是觉得挺好的,万一哪天就用着了,所以果断转载啦~这里附上原创作者的地址:https://www.jianshu.com/p/f15ad28ce3d1
1、概述
缩小图像(或称为下采样(subsampling)或降采样(downsampling))的主要目的有两个:1、使得图像符合显示区域的大小;2、生成对应图像的缩略图。
放大图像(或称为上采样(upsampling)或图像插值(interpolating))的主要目的是放大原图像,从而可以显示在更高分辨率的显示设备上。对图像的缩放操作并不能带来更多关于该图像的信息,因此图像的质量将不可避免地受到影响。然而,确实有一些缩放方法能够增加图像的信息,从而使得缩放后的图像质量超过原图质量的。
下采样原理:对于一幅图像I尺寸为M x N,对其进行s倍下采样,即得到(M/s)x(N/s)尺寸的得分辨率图像,当然s应该是M和N的公约数才行,如果考虑的是矩阵形式的图像,就是把原始图像s*s窗口内的图像变成一个像素,这个像素点的值就是窗口内所有像素的均值:
上采样原理:图像放大几乎都是采用内插值方法,即在原有图像像素的基础上在像素点之间采用合适的插值算法插入新的元素。
无论缩放图像(下采样)还是放大图像(上采样),采样方式有很多种。如最近邻插值,双线性插值,均值插值,中值插值等方法。
2、深度学习中的上采样
在深度学习框架中,上采样可以简单的理解为任何可以让图像变成更高分辨率的技术。
上采样(upsampling)的三种方式:插值法 (Interpolation) 、反卷积 (Deconvolution) 和 反池化 (unPooling) 。
1. 插值法
最简单的方式是重采样和插值:将输入图片input image进行rescale到一个想要的尺寸,而且计算每个点的像素点,使用如双线性插值 (Bilinear-Interpolation) 等插值方法对其余点进行插值。在AlexNet中就使用了较合适的插值方法。各种插值方法都有各自的优缺点。插值就是在不生成像素的情况下增加图像像素大小的一种方法,在周围像素色彩的基础上用数学公式计算丢失像素的色彩(也有的有些相机使用插值,人为地增加图像的分辨率)。所以在放大图像时,图像看上去会比较平滑、干净。但必须注意的是插值并不能增加图像信息。
2. 反卷积
反卷积,是卷积的逆过程,实现上采用转置卷积核的方法,又称作转置卷积 (transposed convolution)。为实现deconvolution,直接使deconv的前向传播模拟conv的反向传播。如何理解深度学习中的deconvolution networks
FCN的upsampling过程,就是把feature map,abcd进行一个反卷积,得到的新的feature map和之前对应的encoder feature map 相加。参考 FCN全卷积网络。
3. 反池化
反池化,在池化过程中,记录下max-pooling在对应kernel中的坐标,在反池化过程中,将一个元素根据kernel进行放大,根据之前的坐标将元素填写进去,其他位置补0。 unPooling是在CNN中常用的来表示max pooling的逆操作。实现代码可以看SegNet的实现,TF-SegNet代码实现,参考 卷积神经网络CNN——SegNet。
训练GAN的16 tricks 参考ICCV 2017 slides
4. 上采样三种方法对比
图(a)表示反池化(unPooling)的过程,特点是在Maxpooling的时候保留最大值的位置信息,之后在unpooling阶段使用该信息扩充feature Map,除最大值位置以外,其余补0。
图(b)表示unSampling的过程,与图(a)对应,两者的区别在于unSampling阶段没有使用MaxPooling时的位置信息,而是直接将内容复制来扩充feature Map。从图中即可看到两者结果的不同。
图(c)为反卷积(Deconvolution)的过程,最大的区别在于反卷积过程是有参数要进行学习的(类似卷积过程),理论是反卷积可以实现UnPooling和unSampling,只要卷积核的参数设置的合理。
5. 常用的插值方法
(1). 最邻近元法(Nearest Neighbour Interpolation)
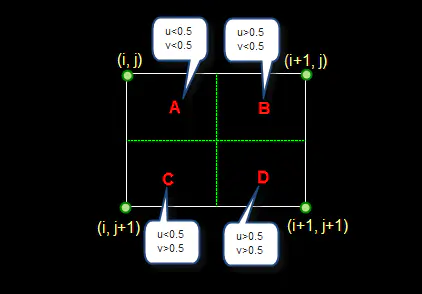
这是最简单的一种插值方法,不需要计算,在待求象素的四邻象素中,将距离待求象素最近的邻象素灰度赋给待求象素。设i+u, j+v(i, j为正整数, u, v为大于零小于1的小数,下同)为待求象素坐标,则待求象素灰度的值 f(i+u, j+v) 如下图所示:
如果(i+u, j+v)落在A区,即u<0.5, v<0.5,则将左上角象素的灰度值赋给待求象素,同理,落在B区则赋予右上角的象素灰度值,落在C区则赋予左下角象素的灰度值,落在D区则赋予右下角象素的灰度值。
最邻近元法计算量较小,但可能会造成插值生成的图像灰度上的不连续,在灰度变化的地方可能出现明显的锯齿状。当图片放大时,缺少的像素通过直接使用与之最接近的原有的像素的颜色生成,也就是说照搬旁边的像素,这样做的结果是产生了明显可见的锯齿。
(2). 双线性内插法(Bilinear Interpolation)
双线性插值是通过周边的四个点,计算权值,然后决定插入后的图像的像素值。新生成的图像中每个点都会计算一遍,是利用待求象素四个邻象素的灰度在两个方向上作线性内插,如下图所示:
对于 (i, j+v),f(i, j) 到 f(i, j+1) 的灰度变化为线性关系,则有:
f(i, j+v) = [f(i, j+1) - f(i, j)] * v + f(i, j)
同理对于 (i+1, j+v) 则有:
f(i+1, j+v) = [f(i+1, j+1) - f(i+1, j)] * v + f(i+1, j)
从f(i, j+v) 到 f(i+1, j+v) 的灰度变化也为线性关系,由此可推导出待求象素灰度的计算式如下:
f(i+u, j+v) = (1-u) * (1-v) * f(i, j) + (1-u) * v * f(i, j+1) + u * (1-v) * f(i+1, j) + u * v * f(i+1, j+1)
双线性内插法的计算比最邻近点法复杂,计算量较大,但没有灰度不连续的缺点,结果基本令人满意。双线性插值算法(Bilinear Interpolation)输出的图像的每个像素都是原图中四个像素(2×2)运算的结果,这种算法极大地消除了锯齿现象它具有低通滤波性质,使高频分量受损,图像轮廓可能会有一点模糊。
(3). 双三次插值算法(Bicubic Interpolation)
是双线性内插法算法的改进算法,它输出图像的每个像素都是原图16个像素(16×16)运算的结果。该方法利用三次多项式S(x)求逼近理论上最佳插值函数sin(x)/x, 其数学表达式为:
待求像素(x, y)的灰度值由其周围16个灰度值加权内插得到,如下图:
待求像素的灰度计算式如下:f(x, y) = f(i+u, j+v) = ABC
三次曲线插值方法计算量较大,但插值后的图像效果最好。
(4). 分形插值算法(Fractal Interpolation)
分形算法(Fractal Interpolation)是Altamira Group提出的一种算法,这种算法得到的图像跟其他算法相比更清晰锐利。
Fractal Interpolation
github fractal_interpolation
tensorflow-fractal-playground
分形与混沌
Curve fitting by fractal interpolation
Python生成简单分形
经典的分形算法
(5). 插值方法总结:
“Inverse Distance to a Power(反距离加权插值法)”、
“Kriging(克里金插值法)”、
“Minimum Curvature(最小曲率)”、
“Modified Shepard's Method(改进谢别德法)”、
“Natural Neighbor(自然邻点插值法)”、
“Nearest Neighbor(最近邻点插值法)”、
“Polynomial Regression(多元回归法)”、
“Radial Basis Function(径向基函数法)”、
“Triangulation with Linear Interpolation(线性插值三角网法)”、
“Moving Average(移动平均法)”、
“Local Polynomial(局部多项式法)”
a. 距离倒数乘方法
距离倒数乘方格网化方法是一个加权平均插值法,可以进行确切的或者圆滑的方式插值。方次参数控制着权系数如何随着离开一个格网结点距离的增加而下降。对于一个较大的方次,较近的数据点被给定一个较高的权重份额,对于一个较小的方次,权重比较均匀地分配给各数据点。
计算一个格网结点时给予一个特定数据点的权值与指定方次的从结点到观测点的该结点被赋予距离倒数成比例。当计算一个格网结点时,配给的权重是一个分数,所 有权重的总和等于1.0。当一个观测点与一个格网结点重合时,该观测点被给予一个实际为 1.0 的权重,所有其它观测点被给予一个几乎为 0.0 的权重。换言之,该结点被赋给与观测点一致的值。这就是一个准确插值。
距离倒数法的特征之一是要在格网区域内产生围绕观测点位置的"牛眼"。用距离倒数格网化时可以指定一个圆滑参数。大于零的圆滑参数保证,对于一个特定的结 点,没有哪个观测点被赋予全部的权值,即使观测点与该结点重合也是如此。圆滑参数通过修匀已被插值的格网来降低"牛眼"影响。
b. 克里金法
克里金法是一种在许多领域都很有用的地质统计格网化方法。克里金法试图那样表示隐含在你的数据中的趋势,例如,高点会是沿一个脊连接,而不是被牛眼形等值线所孤立。
克里金法中包含了几个因子:变化图模型,漂移类型 和矿块效应。
c. 最小曲率法
最小曲率法广泛用于地球科学。用最小曲率法生成的插值面类似于一个通过各个数据值的,具有最小弯曲量的长条形薄弹性片。最小曲率法,试图在尽可能严格地尊重数据的同时,生成尽可能圆滑的曲面。
使用最小曲率法时要涉及到两个参数:最大残差参数和最大循环次数参数来控制最小曲率的收敛标准。
d. 多元回归法
多元回归被用来确定你的数据的大规模的趋势和图案。你可以用几个选项来确定你需要的趋势面类型。多元回归实际上不是插值器,因为它并不试图预测未知的 Z 值。它实际上是一个趋势面分析作图程序。
使用多元回归法时要涉及到曲面定义和指定XY的最高方次设置,曲面定义是选择采用的数据的多项式类型,这些类型分别是简单平面、双线性鞍、二次曲面、三次曲面和用户定义的多项式。参数设置是指定多项式方程中 X 和 Y组元的最高方次 。
e. 径向基本函数法
径向基本函数法是多个数据插值方法的组合。根据适应你的数据和生成一个圆滑曲面的能力,其中的复二次函数被许多人认为是最好的方法。所有径向基本函数法都 是准确的插值器,它们都要为尊重你的数据而努力。为了试图生成一个更圆滑的曲面,对所有这些方法你都可以引入一个圆滑系数。你可以指定的函数类似于克里金 中的变化图。当对一个格网结点插值时,这些个函数给数据点规定了一套最佳权重。
f. 谢别德法
谢别德法使用距离倒数加权的最小二乘方的方法。因此,它与距离倒数乘方插值器相似,但它利用了局部最小二乘方来消除或减少所生成等值线的"牛眼"外观。谢别德法可以是一个准确或圆滑插值器。
在用谢别德法作为格网化方法时要涉及到圆滑参数的设置。圆滑参数是使谢别德法能够象一个圆滑插值器那样工作。当你增加圆滑参数的值时,圆滑的效果越好。
g. 三角网/线形插值法
三角网插值器是一种严密的插值器,它的工作路线与手工绘制等值线相近。这种方法是通过在数据点之间连线以建立起若干个三角形来工作的。原始数据点的连结方法是这样:所有三角形的边都不能与另外的三角形相交。其结果构成了一张覆盖格网范围的,由三角形拼接起来的网。
每一个三角形定义了一个覆盖该三角形内格网结点的面。三角形的倾斜和标高由定义这个三角形的三个原始数据点确定。给定三角形内的全部结点都要受到该三角形的表面的限制。因为原始数据点被用来定义各个三角形,所以你的数据是很受到尊重的。
h. 自然邻点插值法
自然邻点插值法(NaturalNeighbor)是Surfer7.0才有的网格化新方法。自然邻点插值法广泛应用于一些研究领域中。其基本原理是对于 一组泰森(Thiessen)多边形,当在数据集中加入一个新的数据点(目标)时,就会修改这些泰森多边形,而使用邻点的权重平均值将决定待插点的权重, 待插点的权重和目标泰森多边形成比例。实际上,在这些多边形中,有一些多边形的尺寸将缩小,并且没有一个多边形的大小会增加。同时,自然邻点插值法在数据点凸起的位置并不外推等值线(如泰森多边形的轮廓线)。
i. 最近邻点插值法
最近邻点插值法(NearestNeighbor)又称泰森多边形方法,泰森多边形(Thiesen,又叫Dirichlet或Voronoi多边形)分析法是荷兰气象学家A.H.Thiessen提出的一种分析方法。最初用于从离散分布气象站的降雨量数据中计算平均降雨量,现在GIS和地理分析中经常采 用泰森多边形进行快速的赋值。实际上,最近邻点插值的一个隐含的假设条件是任一网格点p(x,y)的属性值都使用距它最近的位置点的属性值,用每一 个网格节点的最邻点值作为待的节点值。当数据已经是均匀间隔分布,要先将数据转换为SURFER的网格文件,可以应用最近邻点插值法;或者在一个文 件中,数据紧密完整,只有少数点没有取值,可用最近邻点插值法来填充无值的数据点。有时需要排除网格文件中的无值数据的区域,在搜索椭圆 (SearchEllipse)设置一个值,对无数据区域赋予该网格文件里的空白值。设置的搜索半径的大小要小于该网格文件数据值之间的距离,所有的无数 据网格节点都被赋予空白值。在使用最近邻点插值网格化法,将一个规则间隔的XYZ数据转换为一个网格文件时,可设置网格间隔和XYZ数据的数据点之间的间距相等。最近邻点插值网格化法没有选项,它是均质且无变化的,对均匀间隔的数据进行插值很有用,同时它对填充无值数据的区域很有效。
j. 插值算法分类 补充
对插值算法分类比较混乱,各人有各人的分类算法。文献《图像插值技术综述》中简略的将插值算法分为传统插值、 基于边缘的插值和基于区域的插值3类,作为初学者入门明晰插值算法还是有帮助。
1.传统差值原理和评价
在传统图像插值算法中,邻插值较简单,容易实现,早期的时候应用比较普遍。但是,该方法会在新图像中产生明显的锯齿边缘和马赛克现象。双线性插值法具有平滑功能,能有效地克服邻法的不足,但会退化图像的高频部分,使图像细节变模糊。在放大倍数比较高时,高阶插值,如双三次和三次样条插值等比低阶插值效果好。这些插值算法可以使插值生成的像素灰度值延续原图像灰度变化的连续性,从而使放大图像浓淡变化自然平滑。但是在图像中,有些像素与相邻像素间灰度值存在突变,即存在灰度不连续性。这些具有灰度值突变的像素就是图像中描述对象的轮廓或纹理图像的边缘像素。在图像放大中,对这些具有不连续灰度特性的像素,如果采用常规的插值算法生成新增加的像素,势必会使放大图像的轮廓和纹理模糊,降低图像质量。
2.基于边缘的图像插值算法
为了克服传统方法的不足, 提出了许多边缘保护的插值方法,对插值图像的边缘有一定的增强, 使得图像的视觉效果更好, 边缘保护的插值方法可以分为两类: 基于原始低分辨图像边缘的方法和基于插值后高分辨率图像边缘的方法。基于原始低分辨率图像边缘的方法:( 1)首先检测低分辨率图像的边缘, 然后根据检测的边缘将像素分类处理, 对于平坦区域的像素,采用传统方法插值;对于边缘区域的像素, 设计特殊插值方法, 以达到保持边缘细节的目的。(2)基于插值后高分辨率图像边缘的方法这类插值方法:首先采用传统方法插值低分辨率图像,然后检测高分辨率图像的边缘,最后对边缘及附近像素进行特殊处理, 以去除模糊, 增强图像的边缘。
3.基于区域的图像插值算法
首先将原始低分辨率图像分割成不同区域,然后将插值点映射到低分辨率图像, 判断其所属区域, 最后根据插值点的邻域像素设计不同的插值公式, 计算插值点的值。
3、 深度学习中的下采样
采样层是使用池化 (pooling) 的相关技术来实现的,目的就是用来降低特征的维度并保留有效信息,一定程度上避免过拟合。但是池化的目的不仅仅是这些,还有保持旋转、平移、伸缩不变形等。
采样有最大值采样,平均值采样,求和区域采样和随机区域采样等。池化也是这样的,比如最大值池化,平均值池化,随机池化,求和区域池化等。
池化操作是在卷积神经网络中经常采用过的一个基本操作,一般在卷积层后面都会接一个池化操作,但是近些年比较主流的ImageNet上的分类算法模型都是使用的max-pooling,很少使用average-pooling,这对我们平时设计模型时确实有比较重要的参考作用。
通常来讲,max-pooling的效果更好,虽然max-pooling和average-pooling都对数据做了下采样,但是max-pooling感觉更像是做了特征选择,选出了分类辨识度更好的特征,提供了非线性,根据相关理论,特征提取的误差主要来自两个方面:(1)邻域大小受限造成的估计值方差增大;(2)卷积层参数误差造成估计均值的偏移。一般来说,average-pooling能减小第一种误差,更多的保留图像的背景信息,max-pooling能减小第二种误差,更多的保留纹理信息。average-pooling更强调对整体特征信息进行一层下采样,在减少参数维度的贡献上更大一点,更多的体现在信息的完整传递这个维度上,在一个很大很有代表性的模型中,比如说DenseNet中的模块之间的连接大多采用average-pooling,在减少维度的同时,更有利信息传递到下一个模块进行特征提取。
但是average-pooling在全局平均池化操作中应用也比较广,在ResNet和Inception结构中最后一层都使用了平均池化。有的时候在模型接近分类器的末端使用全局平均池化还可以代替Flatten操作,使输入数据变成一位向量。
可以参考max-pooling和average-pooling之间的异同
视频的采样方式
1、视频的基本参数
视频分辨率
指每一帧画面的大小,宽乘高等于若干像素。例如某一液晶显示屏的最大分辨率为1440 × 900,而视频文件的分辨率为1024 × 567,那么此视频文件在播放时每个像素点就得经过放大处理,如果放大倍数过多则出现马赛克。
目前主流的高清格式通常为:720p(1280×720)和1080p(1920×1080)还有一种为非主流格式的1080i(1920×1080),1080i和720p对电脑硬件的要求差不多。
实际上720p(1280×720)在分辨率为1440 × 900的显示器的播放时,横向像素的放大人眼根本就看不出来的。所以在选择格式时要视自己终端显示器的最大分辨率到底支持为多高。
码率
即比特率,指单位时间传输的或解码的位数,当然也可以换算成字节,数值越大越好,但是体积会变大的。
码率越高,影像的质量越高,对电脑硬件的要求也越高。蓝光的码率能达到30多M/秒,有的极端的场面达到60M/秒(75930.83 kbs) 。而有的BDre的1080P的码率和720P的码率一样才10多M左右/秒(E.G: 14445.04 kbs)甚至更低。你就发觉质量反而不如720P的(大屏幕上一目了然)。
压制时得在质量与速度两者之间找到一个平衡点,要不配置低的机器播放高码率时就会来不及解析而卡住从而使播放不流畅甚至出现卡死现象。
帧率
指播放时每秒移动多少帧。一般NTSC①是30,PAL②是25,帧速太低则画面不连续播放的流畅性就差.所以要恰到好处才行。
- NTSC制式,又简称为N制,是1952年12月由美国国家电视标准委员会(National Television System Committee,缩写为NTSC)制定的彩色电视广播标准,两大主要分支是NTSC-J与NTSC-US(又名NTSC-U/C)。
- PAL制式是电视广播中色彩调频的一种方法,全名为逐行倒相 (Phase Alternating Line)。除了北美,东亚部分地区使用 NTSC制式 ,中东、法国及东欧采用 SECAM制式 以外,世界上大部份地区都是采用 PAL。
视频在时间上的采样,意味着景物快照的获取足够快,那么当回放时,就会给人连续运动的视频印象。在视频系统中,较为普遍的是使用每秒25~30幅图像,并且广泛被许多观众所接受(在隔行扫描视频中,这个数将加倍)。
音视频图像信号采集卡的采样率
2、深度学习中视频相关采样
动态上采样滤波器
CVPR2018提出,用于视频超分辨率网络。
阅读笔记链接
VSR动态上采样过程的概述如上图所示。首先,将一组输入LR帧{ } (在网络中的7帧:N = 3) 送入动态滤波器生成网络。训练网络输出一组 确定大小(在网络中55)的上采样upsampling过滤器,将用于生成经过滤波器的HR 帧的新的像素。最后,对输入帧中的LR像素进行局部滤波,得到每个输出HR像素值,对应的滤波器如下:
其中,x,y是LR是栅格的坐标,v和u是每个 输出块的坐标 (0 ≤ v, u ≤r − 1),这种操作类似于反卷积(或转置卷积),因此网络可以进行端到端训练。
Frame recurrent video super-resolution (FRVSR) 模型
CVPR2018提出,用于视频超分辨率网络。
在文中作者提出一个端到端可训练的递归帧视频超分辨率(FRVSR)框架。
论文链接Frame-Recurrent Video Super-Resolution
所提出的框架在上图中表示。可训练组件(红色显示)包括光流估计网络FNet和超分辨率网络SRNet。为了产生HR估计,模型利用当前LR输入帧、前一LR输入帧和前一HR估计。利用FNet计算了LR空间中的 ,并将其上采样得到 。
作为第一步,FNet用于估计低分辨率输入和之间的流,从而产生归一化的低分辨率流图。将流图看作一幅图像,使用具有缩放因子s的双线性插值将其放大,从而得到HR流图。使用高分辨率的流程图根据从前一帧到当前帧的光学流对先前估计的图像进行变形。使用空间到深度的转换将变形的先前输出映射到LR空间。在最后一步中,我们将变形前一输出的LR映射与信道维度中的当前低分辨率输入帧连接起来,并将结果馈送到超分辨率网络SRNet。该框架的最终估计是超分辨率网络SRNet的输出。
除了SRNet中使用步长为2进行空间上采样的转置卷积外,这两个网络中的所有卷积都使用带有步长为1的卷积核。
Sub-pixel motion compensation (SPMC)
ICCV2017提出,用于视频超分辨率网络。视频超分辨关注的主要问题有两个:一是如何充分利用多帧关联信息,而是如何有效地融合图像细节到高分辨率图像中。
论文链接Detail-revealing Deep Video Super-resolution
在动作补偿方面,backward warping到参考帧的方法其实并不是最优的。多帧融合方面,虽然很多CNN方法可以产生丰富的细节,但不能确定图像细节是来自内部的帧,还是外部的数据。在可缩放性方面,ESPCN、VSRnet、VESPCN对多尺度超分辨都不太灵活。
基于此,作者提出了一种基于深度学习的视频SR方法,该方法包括亚像素运动补偿sub-pixel motion compensation(SPMC)层,用来有效处理动作补偿和特征图缩放。另外,用一个基于LSTM的框架来处理多帧输入。
作者提出的框架如上图所示。这个网络主要分成三个部分:motion estimation, motion compensation和detail fusion。
动作补偿motion compensation用的就是SPMC层,是一种利用运动中的亚像素信息,同时实现亚像素运动补偿(SPMC)和分辨率增强的新方法。
其中和是输入LR和输出HR图像,F是用于转置翘曲的光流,α是缩放因子。该层包含两个子模块——采样网格生成器和可微的图像采样器,根据和,在放大图像空间中构造输出图像。SPMC层以一个LR图像和一个光流作为输入,可以同时实现运动补偿和分辨率增强。在大多数以前的工作中,它们是分开的步骤(例如,反向翘曲+双三次插值)。
与U-net结构思想有相似之处,但是作者并没有引用。
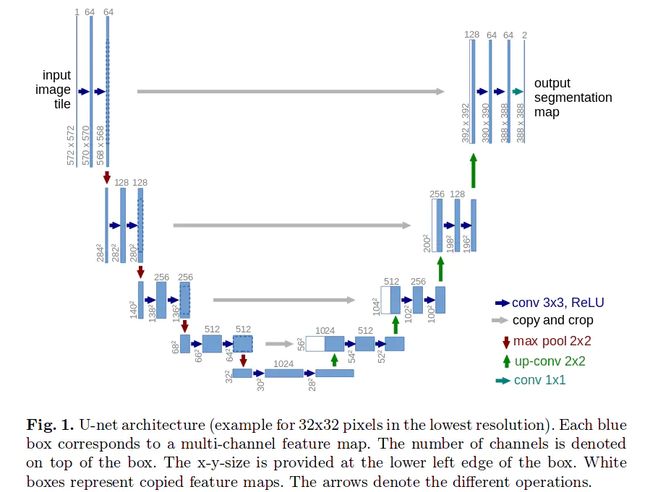
U-Net为了能精准的定位,收缩路径上提取出来的高像素特征会在升采样(upsampling)过程中与新的特征图(feature map)进行结合,以最大程度的保留前面降采样(downsampling)过程一些重要的特征信息。而为了能使网络结构能更高效的运行,结构中是没有全连接层(fully connected layers),这样子可以很大程度上减少需要训练的参数,并得益于特殊的U形结构可以很好的保留图片中的所有信息。
收缩路径上是每两个的卷积层(unpadded convolutional layers)后会跟一个的最大池化层(Maxpooling layer: 步长为2),并且每个卷积层后面采用relu激活函数来对原始图片进行降采样操作,除此之外,每一次降采样都会增加一杯通道数(double the number of feature channel)。
在扩展路径的向上采样(deconvolution)中,每一步会有一个 的卷积层(激活函数也是relu)和一个两个的卷积层,于此同时,每一步的升采样都会加入来自相对应收缩路径的特征图(经裁剪以保持相同的形状shape)。
在网络的最后一层是一个的卷积层,通过这一操作可以将64通道的特征向量转换为所需要的分类结果的数量,最终U-Net的整个网络一共有23层卷积层。U-Net有一个很重要的有点是其基本可以对任意形状大小的图片进行卷积操作,特别是任意大的图片。
Temporal Generative Adversarial Nets (TGAN) 时间生成对抗网络
ICCV2017提出,用于
论文链接Temporal Generative Adversarial Nets with Singular Value Clipping
不同于典型CNN在空间方向上执行二维卷积的,时序生成器 temporal generator中的反卷积层在时间方向上执行一维反卷积。接下来应用反卷积层,扩展它的长度同时减少通道的数量。除通道数和一维反卷积外,反卷积层的设置与图像生成器 image enerator的设置相同。像原始图像生成器一样,在反卷积之后插入一个批归一化(BN)层[13],并使用修正线性单元(ReLU)[23]作为激活函数。
[13] S. Ioffe and C. Szegedy. Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift. arXiv preprint arXiv:1502.03167, 2015.
[23] V. Nair and G. E. Hinton. Rectified Linear Units Improve Restricted Boltzmann Machines.ICML, (3):807–814, 2010.
贝叶斯模型
2014 IEEE TPAMI论文,用于视频超分辨率,是一种估计HR视频序列的贝叶斯方法,该方法同时对运动场和模糊核进行融合。
论文链接A Bayesian Approach to Adaptive Video Super Resolution
香港科技大学Qi Shan在2008年提出一种简单而有效的上采样方法来自动增强图像/视频的分辨率,同时保留必要的结构信息。该方法的主要优点在于反馈控制框架,能够从输入数据中忠实地恢复高分辨率图像信息,而不需要附加从其他例子中学习到的局部结构约束。这使得我们的方法独立于所选例子的质量和数量,这是基于学习的算法的典型问题,同时产生高质量的结果,没有可见的难看的工件。另一个优点是,这个方法自然地扩展到视频上采样,其中时间一致性是自动维护,方法运行快。通过对不同图像/视频数据的实验,验证了算法的有效性。
系统框架。输入图像L最初向上采样,如粉红色框中所示。中间的绿色框和灰色框分别代表反褶积和反馈控制上采样的步骤。
论文链接Fast Image/Video Upsampling
三、语音的采样方式
1、语音采样和量化概述
采样定理又名抽样定理、取样定理、奈奎斯特定理。它是连续时间信号和离散时间信号之间的桥梁,说明了采样频率和信号频谱之间的关系。定理内容:当采样频率fs.max大于信号中最高频率fmax的2倍时(fs.max>2fmax),采样之后的数字信号完整地保留了原始信号中的信息,一般实际应用中保证采样频率为信号最高频率的2.56~4倍。
该定理由奈奎斯特推出,而后信息论的创始人香农又对此加以明确的说明并正式作为定理引用,因此又被称为香农采样定理。
语音信号是一种连续变化的模拟信号,而计算机只能处理和记录二进制的数字信号,因此,由自然音而得的音频信号必须用计算机的声音编辑工具,先进行语音采样,然后利用了计算机上的D转换器,将模拟的声音信号变成离散的量化了的数字信号量化和编码,变成二进制数据后才能送到计算机进行再编辑和存储。语音信号输出时,量化了的数字信号又通过A转换器,把保存起来的数字数据恢复成原来的模拟的语音信号。
当采样频率是原采样频率时,听到的声音是未失真的声音;当降低采样频率时,听到的声音显得比原语音信号要闷(低沉);当增加采样频率时,声音会变得更加尖锐。
每秒从连续信号中提取并组成离散信号的采样个数,也就是计算机每秒钟采集多少个信号样本。采样频率越高,即采样的间隔时间越短,则在单位时间内计算机得到的样本数据就越多,对信号波形的表示也越精确。
下面列举了几个常见的采样率:
8000Hz (8KHz)电话所用采样率,对于人的说话已经足够
11025Hz (11.025KHz)获得的声音称为电话音质,基本上能让你分辨出通话人的声音
22050Hz (22.050KHz)无线电广播所用采样率,广播音质
32000Hz (32KHz)miniDV数码视频camcorder、DAT(LPmode)所用采样率
44100Hz (44.1KHz)音频CD,也常用于MPEG-1音频(VCD,SVCD,MP3)所用采样率
48000Hz (48KHz)miniDV、数字电视、DVD、DAT、电影和专业音频所用的数字声音所用采样率
当前声卡常用的采样频率一般为44.1KHz、1KHz、22KHz和48KHz,采样频率越高,获得的声音文件质量越好,占用存储空间也就越大。一首CD音质的歌曲会占去45M左右的存储空间。
2、深度学习中语音采样方式
NLP上应用的经典采样方法有 Inverse Sampling、Rejective Sampling以及Importance Sampling等。
NLP采样方法
机器学习和自然语言处理
从随机过程到马尔科夫链蒙特卡洛方法
Sampling(采样):
Inverse Sampling(反向采样)
Simple Random Sampling(简单随机采样)
Offline Sampling(离线等可能K采样)
Online Sampling(在线等可能K采样)
Ratio-based Sampling(等比例随机采样)
Acceptance-rejection Sampling(接受-拒绝采样)
Importance Sampling(重要性采样)
MCMC(Markov Chain Monte Carlo 马尔科夫蒙特卡罗采样算法:Metropolis-Hasting& Gibbs)
反向采样 Inverse Sampling
在反向采样(有时称为标准反向采样)中,指的是一直从样本中选取直到事件发生指定次数为止。不知道从多大的样本中采样时,经常使用这个方法。例如,假设正在进行一项野生动物管理调查,想要捕捉20只带状鸟。随机捕捉鸟类,直到收集了20只带状鸟类(还有未知数量的非带状鸟类)。样品的大小可以是100只鸟,也可以是88只鸟,或者203只鸟等。
Paul Lavrakas 在“调查研究方法百科全书”中概述了两种类型的反向抽样:
- 一次矢量采样涉及同时绘制两个观测值(两个观测值中的每一个)。当从其中一个群体获得x成功时,采样停止。
- 获胜者抽样是一次从一个(随机选择的)人群中抽取一个项目。当故障发生时采样停止,然后在第二个人口中继续采样,直到发生故障。此时,采样继续进行,在两个群体之间来回切换,直到发生预定数量的成功。
反向采样的两种基本方法是多反向采样(MIS)和一般反向采样(GIS)。
- 当已知亚种群大小时,使用MIS(最初由Chang及其同事提出)。它的主要优点是避免了后分层中的空层问题。在分层中,选择样本,然后分成层(例如,按性别,年龄或其他特征)。一些选定的阶层最终可能没有条目,特别是如果类别很少。MIS确保每个层中至少有n个项目结束(对每个层次的指定数量的观测值继续采样)。
- GIS避免采样“不可行的单位”(Salehi&Seber)。执行采样,直到分层包含预定数量的单位或直到达到最大样本量。
当特定特征很少时,通常执行反向采样 Inverse sampling。例如,它是检测两种不同治疗罕见疾病之间差异的好方法;避免了由于疾病的罕见而导致数据稀疏的问题。一般而言,只要获得n个体所需的样本大小 n与种群大小N 相比较小,反向采样将为提供比直接采样更精确的估计(Scheaffer等,2011)。但是,因为样本大小是未知的,理论上可能是无限的(在某些情况下),这种技术成本高,劳动强度大,而且耗时。与随机抽样相比,估计的方差通常要大得多。
参考链接 Inverse Sampling
拒绝抽样 Rejective Sampling
在数值分析中,拒绝采样是用于从分布中生成观测值的基本技术。它通常也被称为接受拒绝方法或“接受拒绝算法”,是一种精确的模拟方法。该方法适用于任何分布密度。
拒绝采样基于以下观察:对于随机变量的采样,可以对2D笛卡尔图执行均匀随机采样,并且将样本保持在其密度函数的图的区域中。此属性可以扩展为N维函数。
在学习随机模拟的时候通常会讲到用采样的方法来计算π值,也就是在一个的范围内随机采样一个点,如果它到原点的距离小于1,则说明它在1/4圆内,则接受它,最后通过接受的占比来计算1/4圆形的面积,从而根据公式反算出预估的π值,随着采样点的增多,最后的结果会越精准。
上面这个例子里说明一个问题,想求一个空间里均匀分布的集合面积,可以尝试在更大范围内按照均匀分布随机采样,如果采样点在集合中,则接受,否则拒绝。最后的接受概率就是集合在更大范围的面积占比。
# -*- coding=utf8 -*-
# Code from Chapter 14 of Machine Learning: An Algorithmic Perspective
# The basic rejection sampling algorithm
from pylab import *
from numpy import *
def qsample():
return random.rand()*4.
def p(x):
return 0.3exp(-(x-0.3)**2) + 0.7 exp(-(x-2.)**2/0.3)
def rejection(nsamples):
M = 0.72#0.8
samples = zeros(nsamples,dtype=float)
count = 0
for i in range(nsamples):
accept = False
while not accept:
x = qsample()
u = random.rand()*M
if u<p(x):
accept = True
samples[i] = x
else:
count += 1
print count
return samples
x = arange(0,4,0.01)
x2 = arange(-0.5,4.5,0.1)
realdata = 0.3exp(-(x-0.3)**2) + 0.7 exp(-(x-2.)**2/0.3)
box = ones(len(x2))*0.75#0.8
box[:5] = 0
box[-5:] = 0
plot(x,realdata,‘k’,lw=6)
plot(x2,box,‘k–’,lw=6)
import time
t0=time.time()
samples = rejection(10000)
t1=time.time()
print "Time ",t1-t0
hist(samples,15,normed=1,fc=‘k’)
xlabel(‘x’,fontsize=24)
ylabel(‘p(x)’,fontsize=24)
axis([-0.5,4.5,0,1])
show()
重要性抽样 Importance Sampling
Importance Sample 解决的问题 在深度学习特别是NLP的Language Model中,训练的时候最后一层往往会使用softmax函数并计算相应的梯度。要知道在LM中m的大小是词汇的数量决定的,在一些巨大的模型里可能有几十万个词,也就意味着计算Z的代价十分巨大。softmax函数的表达式是:
而在训练的时候无非是想对softmax的结果进行求导,也就是说
后面这个形式就是与采样相关:
典的蒙特卡洛方法就可以派上用途了,与其枚举所有的词,我们只需要从V里sample出一些样本词,就可以近似地逼近结果了。
同时直接从P中sample也不可取的,而且计算P是非常耗时的事情(因为需要计算Z),我们一般只能计算,而且直接从P中sample也不可取,所以选择另一个分布Q进行Importance Sample即可。一般来说可能选择的Q分布是简单一些的n−gram模型。
一般来说可能选择的Q
分布是简单一些的N元(N-Gram)模型。下面是论文中的算法伪代码,基本上是比较标准的流程。
ClariNet:首个端到端并行音频波形生成模型
论文链接 ClariNet: Parallel Wave Generation in End-to-End Text-to-Speech
代码 github
合成示例Audio samples
ClariNet 还是语音合成领域第一个完全端到端的系统,可以通过单个神经网络,直接将文本转换为原始的音频波形。先前为业界所熟知的端到端音合成系统(比如 Google 提出的 Tacotron ,百度之前提出的 Deep Voice 3 ),实际是先将文本转换为频谱(spectrogram),然后通过波形生成模型WaveNet 或者 Griffin-Lim 算法,将频谱转换成原始波形输出。这种方法由于文本到频谱的模型和 WaveNet 是分别训练优化的,往往导致次优的结果。而百度研究员提出的 ClariNet,则是完全打通了从文本到原始音频波形的端到端训练,实现了对整个 TTS 系统的联合优化,比起分别训练的模型,在语音合成的自然度上有大幅提升。另外,ClariNet 是全卷积模型,训练速度比起基于循环神经网络(RNN)的模型要快 10 倍以上。
ClariNet 的网络结构如下图所示。它使用基于注意力机制(Attention)的编码器-解码器(Encoder-Decoder)模块来学习文本字符与频谱帧之间的对齐关系。解码器的隐状态(hidden states)被送给 Bridge-net 来进行时序信息处理和升采样(upsample)。最终 Bridge-net 的隐状态被送给音频波形生成模块(Vocoder),用来最终合成原始音频波形。