Python 实现图像快速傅里叶变换和离散余弦变换
图像的正交变换在数字图像的处理与分析中起着很重要的作用,被广泛应用于图像增强、去噪、压缩编码等众多领域。本文手工实现了二维离散傅里叶变换和二维离散余弦变换算法,并在多个图像样本上进行测试,以探究二者的变换效果。
1. 傅里叶变换
实验原理
对一幅图像进行离散傅里叶变换(DFT),可以得到图像信号的傅里叶频谱。二维 DFT 的变换及逆变换公式如下:

DFT 尽管解决了频域离散化的问题,但运算量太大。从公式中可以看到,有两个嵌套的求和符号,显然直接计算的复杂度为 O ( n 2 ) O(n^2) O(n2) 。为了加快傅里叶变换的运算速度,后人提出快速傅里叶变换(FFT),即蝶形算法,将计算 DFT 的复杂度降低到了 O ( n log n ) O(n\log n) O(nlogn)。
FFT 利用傅里叶变换的数学性质,采用分治的思想,将一个 N N N 点的 FFT,变成两个 N / 2 N/2 N/2 点的 FFT。以一维 FFT 为例,可以表示如下:
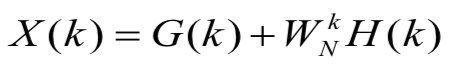

其中, G ( k ) G(k) G(k) 是 x ( k ) x(k) x(k) 的偶数点的 N / 2 N/2 N/2 点的 FFT, H ( k ) H(k) H(k) 是 x ( k ) x(k) x(k) 的奇数点的 N / 2 N/2 N/2 点的 FFT。
这样,通过将原问题不断分解为两个一半规模的子问题,然后计算相应的蝶形运算单元,最终得以完成整个 FFT。
算法步骤
本次实验中,一维 FFT 采用递归实现,且仅支持长度为 2 的整数幂的情况。
算法步骤如下:
- 检查图像的尺寸,如果不是 2 的整数幂则直接退出。
- 对图像的灰度值进行归一化。
- 对图像的每一行执行一维 FFT,并保存为中间结果。
- 对上一步结果中的每一列执行一维 FFT,返回变换结果。
- 将零频分量移到频谱中心,并求绝对值进行可视化。
- 对中心化后的结果进行对数变换,以改善视觉效果。
主要代码
一维 FFT
def fft(x):
n = len(x)
if n == 2:
return [x[0] + x[1], x[0] - x[1]]
G = fft(x[::2])
H = fft(x[1::2])
W = np.exp(-2j * np.pi * np.arange(n//2) / n)
WH = W * H
X = np.concatenate([G + WH, G - WH])
return X
二维 FFT
def fft2(img):
h, w = img.shape
if ((h-1) & h) or ((w-1) & w):
print('Image size not a power of 2')
return img
img = normalize(img)
res = np.zeros([h, w], 'complex128')
for i in range(h):
res[i, :] = fft(img[i, :])
for j in range(w):
res[:, j] = fft(res[:, j])
return res
零频分量中心化
def fftshift(img):
# swap the first and third quadrants, and the second and fourth quadrants
h, w = img.shape
h_mid, w_mid = h//2, w//2
res = np.zeros([h, w], 'complex128')
res[:h_mid, :w_mid] = img[h_mid:, w_mid:]
res[:h_mid, w_mid:] = img[h_mid:, :w_mid]
res[h_mid:, :w_mid] = img[:h_mid, w_mid:]
res[h_mid:, w_mid:] = img[:h_mid, :w_mid]
return res
运行结果
2. 余弦变换
实验原理
当一个函数为偶函数时,其傅立叶变换的虚部为零,因而不需要计算,只计算余弦项变换,这就是余弦变换。离散余弦变换(DCT)的变换核为实数的余弦函数,因而计算速度比变换核为指数的 DFT 要快得多。
一维离散余弦变换与离散傅里叶变换具有相似性,对离散傅里叶变换进行下式的修改:

式中

由上式可见, ∑ x = 0 2 M − 1 f e ( x ) e − j 2 u x π 2 M \sum\limits_{x=0}^{2M-1}f_e(x)e^{\frac{-j2ux\pi}{2M}} x=0∑2M−1fe(x)e2M−j2uxπ 是 2 M 2M 2M 个点的傅里叶变换,因此在做离散余弦变换时,可将其拓展为 2 M 2M 2M 个点,然后对其做离散傅里叶变换,取傅里叶变换的实部就是所要的离散余弦变换。
算法步骤
基于上述原理,二维 DCT 的实现重用了上文中的一维 FFT 函数,并根据公式做了一些修改。
算法步骤如下:
- 检查图像的尺寸,如果不是 2 的整数幂则直接退出。
- 对图像的灰度值进行归一化。
- 对图像的每一行进行延拓,执行一维 FFT 后取实部,乘以公式中的系数,并保存为中间结果。
- 对上一步结果中的每一列进行延拓,执行一维 FFT 后取实部,乘以公式中的系数,返回变换结果。
- 对结果求绝对值,并进行对数变换,以改善视觉效果。
主要代码
二维 DCT
def dct2(img):
h, w = img.shape
if ((h-1) & h) or ((w-1) & w):
print('Image size not a power of 2')
return img
img = normalize(img)
res = np.zeros([h, w], 'complex128')
for i in range(h):
res[i, :] = fft(np.concatenate([img[i, :], np.zeros(w)]))[:w]
res[i, :] = np.real(res[i, :]) * np.sqrt(2 / w)
res[i, 0] /= np.sqrt(2)
for j in range(w):
res[:, j] = fft(np.concatenate([res[:, j], np.zeros(h)]))[:h]
res[:, j] = np.real(res[:, j]) * np.sqrt(2 / h)
res[0, j] /= np.sqrt(2)
return res
运行结果
完整源码请见 GitHub 仓库







