跳跃表(转)
跳跃表
(转自http://www.cppblog.com/superKiki/archive/2010/10/18/130328.html)
本文将总结一种数据结构:跳跃表。前半部分跳跃表性质和操作的介绍直接摘自《让算法的效率跳起来--浅谈“跳跃表”的相关操作及其应用》上海市华东师范大学第二附属中学 魏冉。之后将附上跳跃表的源代码,以及本人对其的了解。难免有错误之处,希望指正,共同进步。谢谢。
跳跃表(Skip List)是1987年才诞生的一种崭新的数据结构,它在进行查找、插入、删除等操作时的期望时间复杂度均为O(logn),有着近乎替代平衡树的本领。而且最重要的一点,就是它的编程复杂度较同类的AVL树,红黑树等要低得多,这使得其无论是在理解还是在推广性上,都有着十分明显的优势。
首先,我们来看一下跳跃表的结构
![]()
跳跃表由多条链构成(S0,S1,S2 ……,Sh),且满足如下三个条件:
每条链必须包含两个特殊元素:+∞ 和 -∞(其实不需要)
S0包含所有的元素,并且所有链中的元素按照升序排列。
每条链中的元素集合必须包含于序数较小的链的元素集合。
操作
一、查找 3. 如果当前位置在最底层的链中(S0),且还要往下移动的话,则输出查询失败 二、插入 我们定义一个随机决策模块,它的大致内容如下: 产生一个0到1的随机数r r ← random() 否则,执行方案B else do B 步骤二:插入高度为4的列,并维护跳跃表的结构 三、删除 目的:从跳跃表中删除一个元素x 在跳跃表中查找到这个元素的位置,如果未找到,则退出 -------------------------------------------------------------------------------- 首先分配一个链表,用list.hdr指向,长度为跳跃表规定的最高层,说是链表,在以下代码中只是分配了一段连续的空间,用来指向每一层的开始位置。我们看到结构体nodeType中,有一个key,一个rec(用户数据),还有一个指向结构体的指针数组。 以下是在网上搜到的一个实现代码
目的:在跳跃表中查找一个元素x
在跳跃表中查找一个元素x,按照如下几个步骤进行:
1. 从最上层的链(Sh)的开头开始
2. 假设当前位置为p,它向右指向的节点为q(p与q不一定相邻),且q的值为y。将y与x作比较
(1) x=y 输出查询成功及相关信息
(2) x>y 从p向右移动到q的位置
(3) x![]()
目的:向跳跃表中插入一个元素x
首先明确,向跳跃表中插入一个元素,相当于在表中插入一列从S0中某一位置出发向上的连续一段元素。有两个参数需要确定,即插入列的位置以及它的“高度”。
关于插入的位置,我们先利用跳跃表的查找功能,找到比x小的最大的数y。根据跳跃表中所有链均是递增序列的原则,x必然就插在y的后面。
而插入列的“高度”较前者来说显得更加重要,也更加难以确定。由于它的不确定性,使得不同的决策可能会导致截然不同的算法效率。为了使插入数据之后,保持该数据结构进行各种操作均为O(logn)复杂度的性质,我们引入随机化算法(Randomized Algorithms)。
如果r小于一个常数p,则执行方案A, if r
初始时列高为1。插入元素时,不停地执行随机决策模块。如果要求执行的是A操作,则将列的高度加1,并且继续反复执行随机决策模块。直到第i次,模块要求执行的是B操作,我们结束决策,并向跳跃表中插入一个高度为i的列。
我们来看一个例子:
假设当前我们要插入元素“40”,且在执行了随机决策模块后得到高度为4
步骤一:找到表中比40小的最大的数,确定插入位置![]()
![]()
删除操作分为以下三个步骤:
将该元素所在整列从表中删除
将多余的“空链”删除 ![]()
我们来看一下跳跃表的相关复杂度:
空间复杂度: O(n) (期望)
跳跃表高度: O(logn) (期望)
相关操作的时间复杂度:
查找: O(logn) (期望)
插入: O(logn) (期望)
删除: O(logn) (期望)
之所以在每一项后面都加一个“期望”,是因为跳跃表的复杂度分析是基于概率论的。有可能会产生最坏情况,不过这种概率极其微小。
以下是自己学习时碰到的一些问题
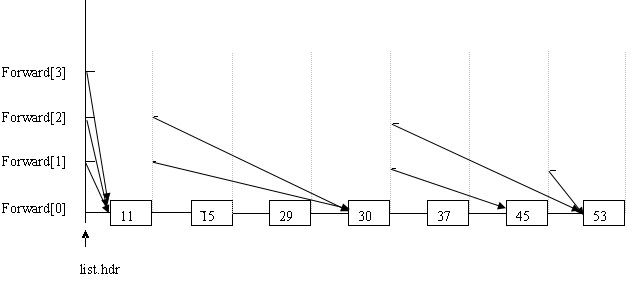
一开始的那些图容易给人误解。如上图所示,例如每个节点的forward[2],就认为是跳跃表的第3层。List.hdr的forward[2]指向11,11的forward[2]指向30,30的forward[2]指向53。这就是跳跃表的第3层:11---30-----53。(准确的说每个forward都指向新节点,新节点的同层forward又指向另一个节点,从而构成一个链表,而数据只有一个,并不是像开始途中所画的那样有N个副本)。本人天资愚钝,看了挺长时间才把它在内存里的结构看清楚了,呵呵。
代码中主要注释了insert函数,剩下的两个函数差不多,就不一一注释了
#include
#include
/*
implementation dependent declarations
*/
typedef
enum {
STATUS_OK,
STATUS_MEM_EXHAUSTED,
STATUS_DUPLICATE_KEY,
STATUS_KEY_NOT_FOUND
} statusEnum;
typedef
int keyType;
/*
type of key
*/
/*
user data stored in tree
*/
typedef
struct {
int stuff;
/*
optional related data
*/
} recType;
#define compLT(a,b) (a < b)
#define compEQ(a,b) (a == b)
/*
levels range from (0 .. MAXLEVEL)
*/
#define MAXLEVEL 15
typedef
struct nodeTag {
keyType key;
/*
key used for searching
*/
recType rec;
/*
user data
*/
struct nodeTag *forward[1];
/*
skip list forward pointer
*/
} nodeType;
/*
implementation independent declarations
*/
typedef
struct {
nodeType *hdr;
/*
list Header
*/
int listLevel;
/*
current level of list
*/
} SkipList;
SkipList list;
/*
skip list information
*/
#define NIL list.hdr
static
int count = 0;
statusEnum insert(keyType key, recType *rec) {
int i, newLevel;
nodeType *update[MAXLEVEL+1];
nodeType *x;
count++;
/*
**********************************************
* allocate node for data and insert in list *
**********************************************
*/
/*
find where key belongs
*/
/*
从高层一直向下寻找,直到这层指针为NIL,也就是说
后面没有数据了,到头了,并且这个值不再小于要插入的值。
记录这个位置,留着向其后面插入数据
*/
x = list.hdr;
for (i = list.listLevel; i >= 0; i--) {
while (x->forward[i] != NIL
&& compLT(x->forward[i]->key, key))
x = x->forward[i];
update[i] = x;
}
/*
现在让X指向第0层的X的后一个节点
*/
x = x->forward[0];
/*
如果相等就不用插入了
*/
if (x != NIL && compEQ(x->key, key))
return STATUS_DUPLICATE_KEY;
/*
随机的计算要插入的值的最高level
*/
for (
newLevel = 0;
rand() < RAND_MAX/2 && newLevel < MAXLEVEL;
newLevel++);
/*
如果大于当前的level,则更新update数组并更新当前level
*/
if (newLevel > list.listLevel) {
for (i = list.listLevel + 1; i <= newLevel; i++)
update[i] = NIL;
list.listLevel = newLevel;
}
/*
给新节点分配空间,分配newLevel个指针,则这个
节点的高度就固定了,只有newLevel。更高的层次将
不会再有这个值
*/
if ((x = malloc(
sizeof(nodeType) + newLevel*
sizeof(nodeType *))) == 0)
return STATUS_MEM_EXHAUSTED;
x->key = key;
x->rec = *rec;
/*
给每层都加上这个值,相当于往链表中插入一个数
*/
for (i = 0; i <= newLevel; i++) {
x->forward[i] = update[i]->forward[i];
update[i]->forward[i] = x;
}
return STATUS_OK;
}
statusEnum delete(keyType key) {
int i;
nodeType *update[MAXLEVEL+1], *x;
/*
******************************************
* delete node containing data from list *
******************************************
*/
/*
find where data belongs
*/
x = list.hdr;
for (i = list.listLevel; i >= 0; i--) {
while (x->forward[i] != NIL
&& compLT(x->forward[i]->key, key))
x = x->forward[i];
update[i] = x;
}
x = x->forward[0];
if (x == NIL || !compEQ(x->key, key))
return STATUS_KEY_NOT_FOUND;
/*
adjust forward pointers
*/
for (i = 0; i <= list.listLevel; i++) {
if (update[i]->forward[i] != x)
break;
update[i]->forward[i] = x->forward[i];
}
free (x);
/*
adjust header level
*/
while ((list.listLevel > 0)
&& (list.hdr->forward[list.listLevel] == NIL))
list.listLevel--;
return STATUS_OK;
}
statusEnum find(keyType key, recType *rec) {
int i;
nodeType *x = list.hdr;
/*
******************************
* find node containing data *
******************************
*/
for (i = list.listLevel; i >= 0; i--) {
while (x->forward[i] != NIL
&& compLT(x->forward[i]->key, key))
x = x->forward[i];
}
x = x->forward[0];
if (x != NIL && compEQ(x->key, key)) {
*rec = x->rec;
return STATUS_OK;
}
return STATUS_KEY_NOT_FOUND;
}
void initList() {
int i;
/*
*************************
* initialize skip list *
*************************
*/
if ((list.hdr = malloc(
sizeof(nodeType) + MAXLEVEL*
sizeof(nodeType *))) == 0) {
printf ("insufficient memory (initList)\n");
exit(1);
}
for (i = 0; i <= MAXLEVEL; i++)
list.hdr->forward[i] = NIL;
list.listLevel = 0;
}
int main(
int argc,
char **argv) {
int i, maxnum, random;
recType *rec;
keyType *key;
statusEnum status;
/*
command-line:
*
* skl maxnum [random]
*
* skl 2000
* process 2000 sequential records
* skl 4000 r
* process 4000 random records
*
*/
maxnum = 20;
random = argc > 2;
initList();
if ((rec = malloc(maxnum *
sizeof(recType))) == 0) {
fprintf (stderr, "insufficient memory (rec)\n");
exit(1);
}
if ((key = malloc(maxnum *
sizeof(keyType))) == 0) {
fprintf (stderr, "insufficient memory (key)\n");
exit(1);
}
if (random) {
/*
fill "a" with unique random numbers
*/
for (i = 0; i < maxnum; i++) key[i] = rand();
printf ("ran, %d items\n", maxnum);
}
else {
for (i = 0; i < maxnum; i++) key[i] = i;
printf ("seq, %d items\n", maxnum);
}
for (i = 0; i < maxnum; i++) {
status = insert(key[i], &rec[i]);
if (status) printf("pt1: error = %d\n", status);
}
for (i = maxnum-1; i >= 0; i--) {
status = find(key[i], &rec[i]);
if (status) printf("pt2: error = %d\n", status);
}
for (i = maxnum-1; i >= 0; i--) {
status = delete(key[i]);
if (status) printf("pt3: error = %d\n", status);
}
return 0;
}