NOIP2016普及组第四题——魔法阵

题目描述

六十年一次的魔法战争就要开始了，大魔法师准备从附近的魔法场中汲取魔法能量。

大魔法师有m个魔法物品，编号分别为1,2,…,m。每个物品具有一个魔法值，我们用Xi表示编号为i的物品的魔法值。每个魔法值Xi是不超过n的正整数，可能有多个物品的魔法值相同。

大魔法师认为，当且仅当四个编号为a,b,c,d的魔法物品满足xa‘<’xb’<’xc’<’xd，Xb-Xa=2(Xd-Xc)，并且xb-xa<(xc-xb)/3时，这四个魔法物品形成了一个魔法阵，他称这四个魔法物品分别为这个魔法阵的A物品，B物品，C物品，D物品。

现在，大魔法师想要知道，对于每个魔法物品，作为某个魔法阵的A物品出现的次数，作为B物品的次数，作为C物品的次数，和作为D物品的次数。

输入输出格式

输入格式：
输入文件的第一行包含两个空格隔开的正整数n和m。

接下来m行，每行一个正整数，第i+1行的正整数表示Xi，即编号为i的物品的魔法值。

保证每个Xi是分别在合法范围内等概率随机生成的。

输出格式：
共输出m行，每行四个整数。第i行的四个整数依次表示编号为i的物品作 为A,B,C,D物品分别出现的次数。

保证标准输出中的每个数都不会超过10^9。

每行相邻的两个数之间用恰好一个空格隔开。

输入输出样例

输入样例#1：
30 8
1
24
7
28
5
29
26
24
输出样例#1：
4 0 0 0
0 0 1 0
0 2 0 0
0 0 1 1
1 3 0 0
0 0 0 2
0 0 2 2
0 0 1 0
输入样例#2：
15 15
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
输出样例#2：
5 0 0 0
4 0 0 0
3 5 0 0
2 4 0 0
1 3 0 0
0 2 0 0
0 1 0 0
0 0 0 0
0 0 0 0
0 0 1 0
0 0 2 1
0 0 3 2
0 0 4 3
0 0 5 4
0 0 0 5
说明

【样例解释1】

共有5个魔法阵，分别为：

物品1,3,7,6，其魔法值分别为1,7,26,29;

物品1,5,2,7，其魔法值分别为1,5,24,26;

物品1,5,7,4，其魔法值分别为1,5,26,28;

物品1,5,8,7，其魔法值分别为1,5,24,26;

物品5,3,4,6，其魔法值分别为5,7,28,29。

以物品5为例，它作为A物品出现了1次，作为B物品出现了3次，没有作为C物品或者D物品出现，所以这一行输出的四个数依次为1,3,0,0。

此外，如果我们将输出看作一个m行4列的矩阵，那么每一列上的m个数之和都应等于魔法阵的总数。所以，如果你的输出不满足这个性质，那么这个输出一定不正确。你可以通过这个性质在一定程度上检查你的输出的正确性。

【数据规模】

---

这题我拿了55分(11个点），这题数据比较大。

这题我是用枚举

我是先用快排，将魔法值从小到大排序出来，再用四个for将每一种情况枚举出来，在判断这四个数符不符合条件。如果符合，就在相应位置上加1。

这题我怕数据爆了，所以就将数据缩小了。

---

代码如下：

var  n,m,i,j,k,w:longint;
     a,b:array[1..400]of longint;
     x:array[1..400,1..4]of longint;

procedure qsort(l,r:longint);
var i,j,mid,t:longint;
begin
  if l>=r then exit;
  i:=l; j:=r; mid:=a[(i+j) div 2];
  repeat
    while mid>a[i] do inc(i);
    while middo dec(j);
    if i<=j then
      begin
        t:=a[i]; a[i]:=a[j]; a[j]:=t;
        t:=b[i]; b[i]:=b[j]; b[j]:=t;
        inc(i);
        dec(j);
      end;
  until i>j;
  qsort(i,r);
  qsort(l,j);
end;

begin
  assign(input,'magic.in');
  assign(output,'magic.out');
  reset(input);
  rewrite(output);
  read(n,m);
  for i:=1 to m do begin read(a[i]); b[i]:=i; end;
  qsort(1,m);
  for i:=1 to m-3 do
    for j:=i+1 to m-2 do
      for k:=j+1 to m-1 do
        for w:=k+1 to m do
          if (a[j]-a[i]=2*(a[w]-a[k]))and(a[i]and(a[j]and(a[k]and(a[j]-a[i]<(a[k]-a[j])/3) then
            begin
              inc(x[b[i],1]);
              inc(x[b[j],2]);
              inc(x[b[k],3]);
              inc(x[b[w],4]);
            end;
  for i:=1 to m do
    begin
      for j:=1 to 4 do write(x[i,j],' ');
      writeln;
    end;
  close(input);
  close(output);
end.

前方高能，100%要来了

---

由原不等式组，我们可以得出，见下图：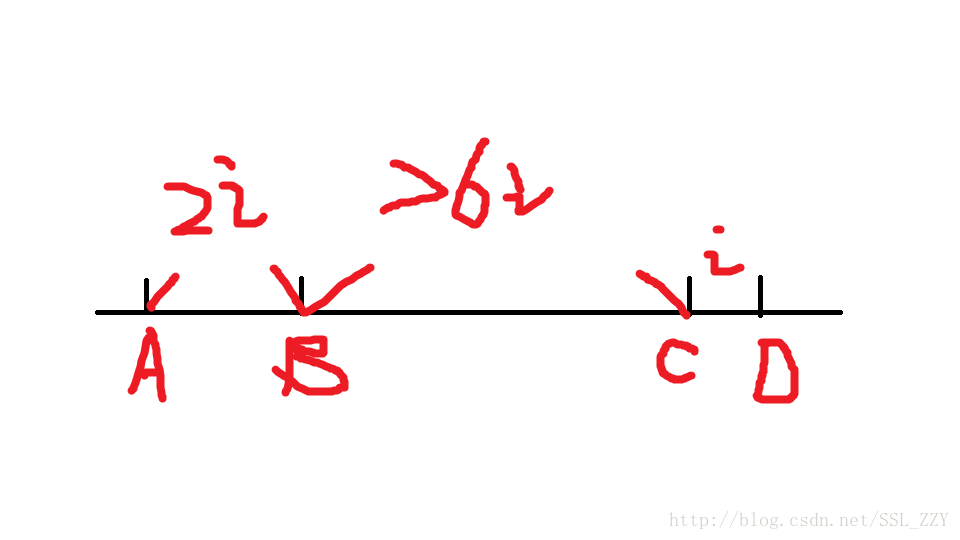

可以先用一个数组，来存当前每一种魔法物品出现的个数
然后我们枚举i，那么i的范围就是[1..i*9< n]
我们枚举两次，一次枚举a，一次枚举d
那么每次枚举，我们就可以求出剩下的三个的位置
如果当前枚举a，那么我们就可以求出a和b的组合数，就可以求出c和d增加了多少
d类似于上

---

代码：

#include
#include
#include
using namespace std;
int n,m,d;
int v[40001][5]={0};
int num[15001]={0};    
int data[40001];
int main()
{
    int i,w;
    scanf("%d%d",&n,&m);
    for(i=1;i<=m;i++)
    {
        scanf("%d",&data[i]);
        num[data[i]]++;
    }
    for(w=1;w*9int sum=0;
        int a,b,c,d;
        for(d=w*9+2;d<=n;d++)
        {
            a=d-9*w-1;    
            b=d-7*w-1;   
            c=d-w;           
            sum+=num[b]*num[a]; 
            v[c][3]+=num[d]*sum;
            v[d][4]+=num[c]*sum;
        }
        sum = 0;
        for(a=n-w*9-1;a>=1;a--)
        {
            b=a+2*w;
            c=a+w*8+1;
            d=a+w*9+1;
            sum+=num[c]*num[d];
            v[a][1]+=num[b]*sum;
            v[b][2]+=num[a]*sum;
        }
    } 
    for(i=1;i<=m;i++) printf("%d %d %d %d\n",v[data[i]][1],v[data[i]][2],v[data[i]][3],v[data[i]][4]);
    return 0;
}

转载于:https://www.cnblogs.com/Comfortable/p/8412477.html