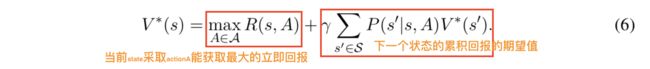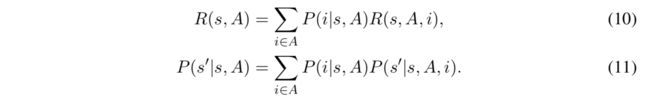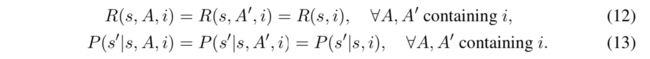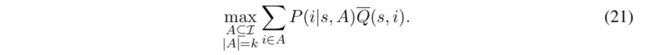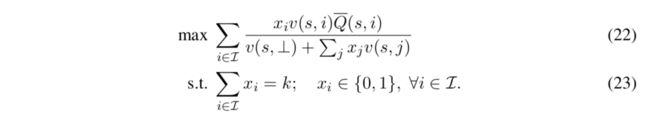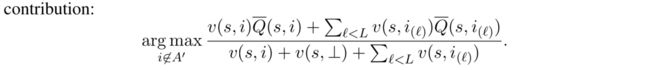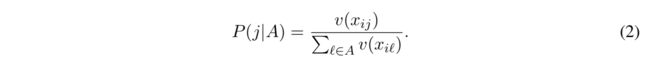强化学习RL应用在youtube推荐系统 2019谷歌论文解读

论文解读：Reinforcement Learning for Slate-based Recommender Systems: A Tractable Decomposition and Practical Methodology

原文链接：https://www.cs.toronto.edu/~cebly/Papers/SlateQ_IJCAI_2019.pdf

• 论文主要贡献：

1、提出了一种名为 SLATE-Q 的 Q-Learning 算法，将一个slate的推荐序列分解成多个items，计算长期收益 LTV（Long-term Value）, 将长期收益加入排序多目标中进行建模优化。（我理解的slate是一个候选列，相当于给用户推荐的item的候选列表。）

引入了几个假设： user choice behavior 和 system dynamics.

分解slate以后减少了TD模型(temporal difference)如Q-learning、SARSA算法的generalization(泛化) and exploration(探索)的复杂度。对于一些特定的choice model, 可以使用optimal LP-based 和 启发式算法：greedy 和 top-k 的方法来解决slate的最优化问题。结果显示SLATEQ的方法有很好的鲁棒性，而且可以运用到大规模的商业系统如youtube。

2、沿用现有的短期回报模型，得到长期回报RL模型的具体的实施方法，并且在youtube上进行实验。

1、Introduction

目前主流的个性化推荐技术的问题：

• 优化的目标都是短期的回报，比如点击率、观看时长，很难对长期收益 LTV(long term value) 建模。
• 最主要的是预测用户的兴趣，但模型都是基于 logged feedback 训练，样本和特征极度稀疏，大量的物料没有充分展示过，同时还是有大量的新物料和新用户涌入，存在大量的 bias。另外，用户的兴趣变化剧烈，行为多样性，存在很多 Noise。
• pigeon-hole：在短期目标下，容易不停的给用户推荐已有的偏好。在另一面，当新用户或者无行为用户来的时候，会更倾向于用大爆款去承接。

强化学习(RL)应用在推荐系统

众所周知，RL 是典型的需要海量数据的场景，比如著名的 AlphaGo 采用了左右互博的方式来弥补训练数据不足的问题。但是在推荐场景，用户和系统的交互是动态的，即无法模拟。举个例子，你不知道把一个没有推荐过的商品 a 给用户，用户会有什么反馈。

• 极大的action space：many millions of items to recommend。推荐给用户的选择有成千上万，且推荐给用户的是一系列的items，是一个组合问题，让action space更加复杂。
• 由于是动态环境，无法确认给用户看一个没有看过的item，用户的反馈会是什么，所以无法有效模拟，训练难度增加。
• 本质上都要预估 user latent state，但存在大量的 unobersever 样本和noise，预估很困难，这个问题在 RL 和其他场景中共存。
• long term reward 难以建模，且 long/short term reward。tradeoff due to user state estimate error。

2、Related work

Recommender Systems 推荐系统

基于协同过滤的推荐系统是最为常见的。这里不过多做介绍。

序列模型和RL推荐系统

User Choice Behavior 用户选择行为建模

优化推荐序列的问题取决于用户选择行为，主要的模型有multinomial logit (MNL)

和它的拓展conditional logit model等。

RL with Combinatorial Action Spaces

Sequential DQN

Slate MDPs

3、MDP模型 马尔可夫决策过程

RL 最大的特点是和环境的交互，是一种 trial-error 的过程，通常我们会用 MDP 来描述整个过程，结合推荐场景，四元组数学定义如下：

• S ：state，用户状态
  • 静态（声明的用户兴趣、属性）和动态特征（用户的context）
  • 用户的反馈、接受的建议、用户的响应（接受或拒绝的推荐）、用户参与度
• A：action，给用户推荐的item，离散空间
• P(s’|s,A)： S × A × S → R，状态转换的概率，在状态s下采取A时，转移到状态s‘的概率。反映了用户response和环境因素的不确定性。
• R：S × A → R，reward function，即刻的回报，文章用用户的参与度来建模。（需要考虑到用户回应的不确定性）

函数定义：

• value function：

• 训练出最优的value function：

• q-function：

• 训练出最优的q-function：

• SARSA的方法更新q-value（on-policy）：

  $Q^{(t)}$：第t次迭代$Q^{\pi }$的预测值

  $\alpha$: 学习率

• Q-learning的是off-policy：

4、Slate-Q：候选值的分解

上述公式的问题：用户的action space复杂度过大，数据需要压缩表示，需要找到一个组合的优化的问题最优解。

提出一个计算Q-value的方法：Slate-Q。

通过将一个slate(候选列)的LTV分解成item级别的LTVs，支持了有效率的TD-learning，并且重点建模了user choice modle。

这个 itemwise 和我们常规理解的 pointwise 的个性化技术还是有区别的，在于这个 wise 是 reward 上的表达，同时要引申出 user choice model 。pointwise 的方法只考虑单个 item 的概率， itemwise虽然也是认为最后的 reward 只和每个被选中的 item 有关，且 item 直接不互相影响，但它有对 user choice 做假设。将目标函数的优化变成一个多项式内可解的问题。

• SC（Single choice） ：一个用户从候选列中每次只选择一个item(可能是null ⊥).

  • 用R(s, A, i)表示用户在状态s下，采取候选序列A，选择第i个item的reward。

    P (s′ |s, A, i)同理，于是reward可以用一下的累加和式子表示。

• RDTS （Reward/transition dependence on selection）：得到的回报或着状态转换R(s, A)、P (s′ |s, A) 只和当前选择的 item 有关。

  我们可以假设用户的行为不会受一个slate A中未被选中的item的影响，则得到如下的简化式子。

用一个item级别的辅助函数${\overline{Q}}^{\pi }$，表示了用户消费一个item的LTV，并且与slate A无关，只和单个item有关。

于是结合SC的假设，有如下结论：

更新公式：

最终会收敛到最优的$Q^{\ast }(s,A)$

5、用Q-values 优化 Slate

为了让Q-learning可行，必须需要解一个combinatorial slate optimization problem（组合slate的最优化问题）—— 即给定一个每个item的Q-value，找到一个有最大LTV的slate。

运用了一个 fractional mixed-integer programming公式来优化slate，然后用formulation和relaxation使得问题能够得到线性规划的解决。

还提出了两个启发算法：top-k和greedy的slate构造，虽然没有理论依据，但在实验中跑的很好。

1.Exact Optimization算法

需要最大化如下值：

结论：在sc假设下能在多项式时间内解出结果。

具体最优化的计算过程取决于choice model的具体形式，文章采用了conditional logit model (CLM) 来进行计算。

• $x_{ij}$ :用户i选择item j 的概率

选择item基于的是item的LTV or Q-value,而不是它对用户的即刻的吸引力。

假设用户在s状态下以v(s,i)的概率选择了item i，

最优化公式（把$P(j|A)$代入）：

以上问题是classic product-line的变体，可以运用 assortment optimization or product line design的方法来解，转换为线性规划的问题：

Chen and Hausman [2000]论文讨论了解法。

2.Top-k 和 Greedy 算法

避免LP(线性规划)问题在serving阶段计算。

一个启发式的算法是得到将k个items直接相加的最高的score。

• Top-k optimization ：

将item的以$v(s,i)\overline{Q}(s,i)$的值的降序排列插入到slate里面。时间复杂度由 $O(log(I))$变成 $O(I)$ 。

• Greedy optimization：

  根据现在的slate更新item的分数。比如给定$A\prime =i_{(1)},...i_{(L-1)},$ $L−1 < k, $被加入的第L个itemitem 是以下式子的最大值：边际贡献值

6、模拟用户环境

提出了一个推荐系统的模拟环境，RecSim，支持直接的item配置，用户state模型，用户选择模型。

1、document和topic模型

• $D$：一个documents的结合，表示可以推荐的内容，

  $d\in [0,1{]}^{|T|}$，$d_j$表示d和topic j的关联程度。

  $l(d)$：d的长度，实验中是固定长度l

  $L_d$：文章的质量度量，遵循正态分布$N({\mu }_{T(d)},{\sigma }^s)$

• T：topics的集合，捕捉了用户兴趣的基本特点

2、User Interest and Satisfaction模型

用户$u\in U$ ：表示user对topic的感兴趣程度向量。$u\in [-1,1{]}^{|T|}$

$I(u,d)=ud$ ：用户对document d 的兴趣通过点乘。

$S(u,d)=f(I(u,d),L_d)$：用户对document d的满意程度。本文用的函数是$S(u,d)=(1-\alpha )I(u,d)+\alpha L_d,\alpha =1$,也可以使用更加复杂的函数。

3、User choice模型

给定一个slate的document，该模型影响着用户会选择哪个document。假设用户在选择之前可以观察document的topic，但不能知道它的质量，在选择完之后可以知道文章质量。

$I(u,d)=ud$：定义了用户对document的感兴趣程度。

在模拟实验中用的模型是general conditional choice model

本文还是用了另一个choice模型—— exponential cascade model[Joachims, 2002]。这里不过多做介绍。

4、动态用户模型

1、剩余时间模型：假设每个用户u有一个初始的时间预算$B_u$，并且推荐系统不能感知到这个预算。每个document d会减少时间预算，由document的长度l计算而出。 但是更高质量的文章会消耗的budget更慢一些，它会在用户消耗l的时候再增加奖励b，用S(u,d)满意程度计算出来。

在实验中取，初始时间预算$B_u=200$ 单位;每个document消耗 $l=4$ 单位; 如果一个slate里没有被选择的document，则消耗0.5单位的时间。奖励$ b = \frac {0.9}{3.4} · l · S(u, d). $

2、用户兴趣会随着看过的文章改变。

$t = T (d) $：表示document d的topic

$I_t$ :表示用户u对topic t的兴趣

$∆t(I_t)=(-y|I_t|+y)\cdot -I_t,y\in [0,1]$ 来更新$I_t$

5、推荐系统动态模型

在每一轮和用户的互动中，从$P_D$中取m个候选documents，并且一个slate包含的k个items必须被选入推荐当中。在大规模的商业应用中，需要从大量的语料库中选择一组小的候选序列，然后用更加精确的方式（计算成本更高）来进行评分。

在模拟实验中，取m = 10 ， k = 3。

7、经验估计

使用了一个标准的 two-tower architecture 运用堆叠的全连接层来表示用户状态和文档。 Q-models 的更新通过模拟用户在线上完成。

8 、实作的方法

很多item级别的推荐系统有由如下部分组成：

1. Logging：用户的反馈和impression的log。
2. Training：训练回归模型（如DNN）来预测 用户的response，由一些scoring函数聚合而成;
3. Serving：推荐和排序，选择top k个items。

1.状态空间（state space）的建立

用户的历史记录提取出的特征。

2.用户的generlization

建模用户的features来generlize用户，目前的推荐系统可以做到这一点。

3.用户response的建模

用第4、5节的SLATE-Q来建模。目前的推荐系统预测的是immediate的回报，例如pCTR模型。

4.Logging，Training，Serving的基础

LTV Qπ (s, a) 的训练基于用户数据的log，和基于LTV分数的实时推荐服务serving。

在后面的实验中我们用的是SARSA算法。在短期推荐系统中，回归模型预测用户的immediate response，而在我们的长期推荐系统中，label generation提供了LTV 标签，让regressor来建模${\overline{Q}}^{\pi }$

模型周期性训练并推送到server上，ranker利用最新的模型来推荐items，记录user的反馈，反馈用于训练新的模型。用了LTV labels的迭代模型训练和推送可以看作一种generalized policy iteration。 每个训练好的DNN表示了前一个batch的value(policy evaluation)。Ranker 按照value函数贪心选择( policy improvement)。

LTV label generation 类似 DQN的训练[Mnih et al., 2015]。LTV labels是用分开的网络进行训练的，周期性地将main网络的参数拷贝到label网络。label网络的更新方法：

9、训练流程

本文在youtube上使用 SARSA-TS算法，特别地用了 SLATEQ decomposition算法，来实现大规模的视频推荐。系统由两个部分组成 candidate generator取回最符合用户内容的部分items（几百个）。 ranker使用DNN对选出的items进行分数的计算和排名。

本文的非短期推荐系统使用用户在N天的点击轨迹来最大化累积的engagement，我们使用基于时间的discount来处理时间跨度很大的credit assignment。 如果在$t_1$和$t_2$之间有连续访问，则discount of $t_2$ 的值是 ${\gamma }^{(t_2-t_1)/c},$c是一个控制时间尺度的参数。

具体的，我们用了一个 multi-task feedforward deep network（多任务深度前馈网络）来学习：$\overline{Q}(s,i)$、用户的在state s下长期pCTR概率、短期回报v(s, i) 等。网络有4个隐层，大小分别为2048，1024，512，256,每个隐层用了ReLU activation函数。

在serving阶段，我们不仅使用了top-k的方法来选择slate，还根据score：$v(s,i){\overline{Q}}^{\pi }(s,i)$来对slate排序。

以下是模型训练流程，用的是随机梯度下降，

1.参数

• T：迭代次数
• M：更新label 网络的间隔
• $\gamma$：discount rate
• ${\theta }_{main}$：主神经网络参数
• ${\overline{Q}}_{main}$：用户long-term value的预测值
• ${\theta }_{label}$：标签（目标）神经网络参数
• ${\theta }_{pctr}$：预测网络items的pCTR（点击率预测）的参数

2.输入：$D_{training}=(s,A,C,L_{myopic},s^{\prime },A^{\prime })$

• s:当前状态的特征向量，s’:下一个状态的特征向量，
• $A=(a_1,...,a_k)$:当前状态的推荐slate，$A^{\prime }=(a_1^{\prime },...,a_k^{\prime })$:下一个状态的推荐slate
• $C=(c_1,...,c_k)$: $c_i$代表第i个item是否被点击。
• $L_{myopic}=(l_{myopic}^1,...,l_{myopic}^k):$短期的label。（短期回报）

3.输出训练好的${\overline{Q}}_{main}$,预测用户的long-term value。

4.初始化${\theta }_{label}=0,$随机初始化${\theta }_{main}$和${\theta }_{pctr}$