最新版学习笔记--Python机器学习基础教程（8）核支持向量机-- 附完整代码

正在学习书上的内容，书上有部分代码没有给全，注解不详细，且随着版本原因出现的问题有所调整，所以写下学习笔记供大家参考。

1、环境搭建

python版本最好是3.6.x及以上，我这里用的是3.7.1版本
安装有机器学习库sklearn、mglearn、matplotlib、numpy，若没有用pip安装

pip install sklearn
pip install mglearn
pip install matplotlib
pip install numpy

2、出现的问题

• mpl_toolkits这个包跟随matplotlib库，只要安装matplotlib就可以调用mpl——toolkits
• 关于scatter函数的参数用法见之前的博文

3、线性模型与非线性特征

线性模型在低维空间中可能非常受限，因为线和平面的灵活性有限。有一种方法可以让线性模型变得更加灵活，就是添加更多的特征。

我们下来看一下，我们上一次讲决策树集成所用到的数据

from sklearn.datasets import make_blobs
import mglearn
import matplotlib.pyplot as plt
X,y = make_blobs(centers=4,random_state=8)
y=y%2
mglearn.discrete_scatter(X[:,0],X[:,1],y)
plt.xlabel("Feature 0")
plt.ylabel("Feature 1")
plt.show()

效果图：

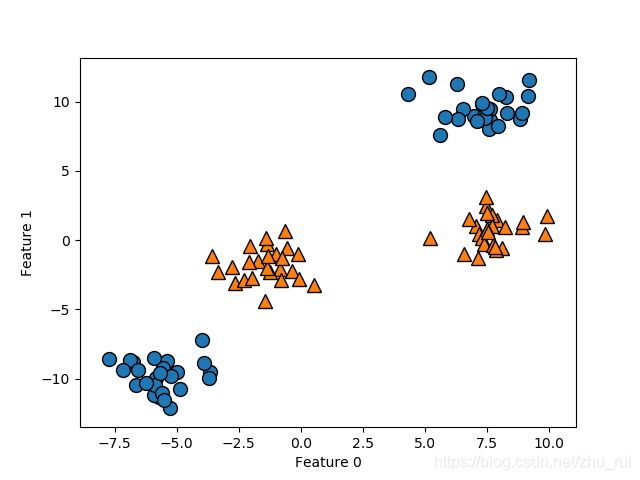
可以明确的了解到用于分类的线性模型对这个数据集无法给出较好的结果，因为其只能通过一条直线划分数据点。
所以我们可以对输入的特性进行扩展，比如说添加第二个特征的平方作为一个新的特征（feature 1 ** 2）。现在我们将每个数据点表示位三维点（feature0，feature1，feature1**2）。现在我们编写代码看一下效果。代码如下：

from mpl_toolkits.mplot3d import Axes3D,axes3d
import numpy as np
import matplotlib.pyplot as plt
import mglearn
from sklearn.datasets import make_blobs
X,y = make_blobs(centers=4,random_state=8)
y=y%2
X_new = np.hstack([X,X[:,1:]**2])
figure = plt.figure()
#3D可视化
ax = Axes3D(figure,elev=-152,azim=-26)
#首先画出y=0的所有点，在画出y=1的所有点
mask=y==0
ax.scatter(X_new[mask,0],X_new[mask,1],X_new[mask,2],c='b',cmap=mglearn.cm2,s=60)
ax.scatter(X_new[~mask,0],X_new[~mask,1],X_new[~mask,2],c='r',marker = '^',cmap=mglearn.cm2,s=60)
ax.set_xlabel("feature0")
ax.set_ylabel("feature1")
ax.set_zlabel("feature1**2")
plt.show()

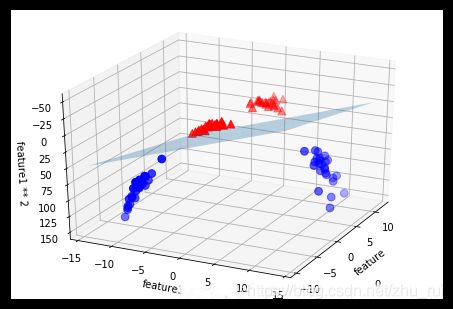
效果图：

从图片中，我们可以在三维空间中用线性模型（平面）将两个类别分开。我们之所以用这个方法，就是因为我们在二维平面无法分类。
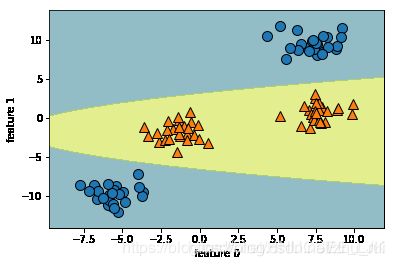
我们运用线性模型你和后的图形如下：

这是一个线性SVM对扩展最后的三维数据集给出的决策边界。
但如果将线性SVM模型看作原始特征额函数，那么它实际上已经不是线性的了。它在二维平面内变成了一个椭圆。如下图：

4、核技巧

向数据表示中添加非线性特征，可以让线性模型变得强大。但是我们通常来说不知道该添加那些模型，并且有可能添加的模型做计算的开销会很大，所有就出现了一种方法——核技巧。核技巧的原理是直接计算扩展特征表示中数据点之间的距离（内积），而不用实际对扩展进行计算。对于支持向量机，将数据映射到更高维的空间中有两种常用方法：一是多项式核，计算原始特征所有可能的多项式；二是径向基函数核（RBF核），也叫高斯核，考虑所有阶数的所有可能的多项式，但阶数越高，特征的重要性越小。

在训练过程中，SVM学习每个训练数据点对于两个类别之间的决策边界的重要性，而位于决策边界上的点叫做支持向量。而对新样本点的预测基于与支持向量之间的距离以及支持向量重要性，此时核技巧的作用就在于对数据点之间的距离的定义，有一种节十是它考虑所有结束的可能的多项式，但阶数越高，特征的重要性就越小。

不过在实践中，核SVM背后的数学细节并不是很重要，可以简单地总结出使用RBF核SVM进行预测的方法。

5、理解SVM

对于SVM来说，它只对位于类别之间边界的那些点来说，用于定义决策边界很重要。那些点也叫作支持向量（支持向量机由此得名）。
想要对新的样本点进行预测，需要测量它与每个支持向量的距离。分类决策是基于它与支持向量之间的距离以及训练过程中学到的支持向量重要性来做出的。
数据点之间的距离由高斯核给出，k(x1, x2) = exp(-γ ||x1 - x2||²)，x1, x2是数据点，||x1 - x2||表示欧式距离，γ是控制高斯核宽度的参数。

6、关于SVM常用参数的调整

我们调用SVM，会用到这个函数语句：

svm =SVM(kernel = ‘rbf’, C=10, gamma=0.1)

• kernel：选择核函数类型（“rbf”：径向基函数，“linear”：线性，“poly”：多项式，“sigmoid”：神经元的非线性作用函数核函数，“precomputed”：用户自定义核函数）。
• C：正则化参数，与线性模型中用到的类似。
• gamma：公式中的γ，默认为1/n_features（特征总数的倒数），用于控制高斯核的宽度，它决定了"点与点"之间靠近的距离，gamma越大，高斯核宽度（半径）越小，点与点距离越大，模型复杂度越高。

我们通过看下面的图片比较C参数和gamma参数的具体联系。

小的gamma值表示决策边界变化很慢，生成的是复杂度较低的模型，而大的gamma值则会生成更复杂的模型。
小的C值，是模型受限，每个数据点的影响有限；大的C值，对模型的影响增大，决策边界从线性变为非线性。

7、SVM的预处理数据

首先我们看一下未处理的时候，训练得到的精度有多少，我们以前文讲的乳腺癌数据集为例。（默认C=1,gamma=1/n_features），运行代码如下：

from sklearn.datasets import load_breast_cancer
from sklearn.model_selection import train_test_split
from sklearn.svm import SVC
cancer = load_breast_cancer()#提取数据
X_train, X_test, y_train, y_test = train_test_split(cancer.data, cancer.target, 
	stratify=cancer.target, random_state=0)#数据分类
svc = SVC().fit(X_train, y_train)#训练数据
print("Accuracy on training set: {:.3f}".format(svc.score(X_train, y_train)))
print("Accuracy on test set: {:.3f}\n".format(svc.score(X_test, y_test)))

输出：

Accuracy on training set: 1.000
Accuracy on test set: 0.629

这个模型在训练集上的精度非常完美，但是在测试集上的精度只有63%，存在严重的过拟合。所以我们要对每个特征进行缩放处理来解决这个问题，也就是预处理。

预处理——对每个特征进行缩放，使其大致都位于同一个范围。核SVM常用的缩放方法就是将所有特征缩放到0核1之间。这个以后会学。。。。。。（这个书上说的，真是个弟弟）现在我们先通过调节参数“人工”做到这一点。

from sklearn.datasets import load_breast_cancer
from sklearn.model_selection import train_test_split
from sklearn.svm import SVC
cancer = load_breast_cancer()#提取数据
X_train, X_test, y_train, y_test = train_test_split(cancer.data, cancer.target, 
	stratify=cancer.target, random_state=0)#数据分类
#计算训练集中每个特征的最小值
min_on_training = X_train.min(axis=0)
#计算训练集中每个特征的范围（最大值-最小值）
range_on_training = (X_train - min_on_training).max(axis=0)
#对每个数据点减去其特征的最小值，然后除以其特征的范围，使得每个特征的数据都在[0, 1]上
X_train_scaled = (X_train - min_on_training) / range_on_training
#利用训练集得出的最小值与范围对测试集做相同的变换
X_test_scaled = (X_test - min_on_training) / range_on_training
svc = SVC().fit(X_train_scaled, y_train)
print("Accuracy on training set: {:.3f}".format(svc.score(X_train_scaled, y_train)))
print("Accuracy on test set: {:.3f}\n".format(svc.score(X_test_scaled, y_test)))

结果：

Accuracy on training set: 0.991
Accuracy on test set: 0.944

完美解决过拟合的问题！