链表插入操作的时间复杂度真的是O(1)吗?
提起链表,很多人可能都会知道它的优势就是能够快速插入、删除数据。但是往链表中插入数据的时间复杂度真的是O(1)吗?相信看完这篇文章,读者会有自己的答案了。
为什么用一节来讲解链表代码实现 ?
1. 链表的代码量虽然不多,但是其中充满了大量的指针操作,所以很考验面试者对指针引用操作的熟练程度。
2. 链表的操作往往需要考虑到对边界问题的考虑,比如在链表是空链表的情况下,代码是否还能正确执行。
这同时考察了一个程序员的编程基本功,也能体现一个程序员在逻辑上是否是足够严谨的,思维是否缜密。所以很面试官在面试的时候都特别青睐询问链表相关的题目。
需要掌握到何种程度
上一节发布之后,很多人私信跟我说: 我已经了解了什么是链表,以及它的特点。难道这就已经足够了吗??代码方面还是写不出来没有关系吗??
链表并不像 红黑树、图算法那样,复杂到几乎不可能在短短的1、2个小时内写出完整并正确的实现代码。相反,链表的创建、插入和删除结点等操作都只需要20行左右的代码就能实现,所以面试官一般都是直接让应聘者手写链表代码的。
基于这个原因,对于链表的基本操作代码,应聘者必须熟练到如同写 Hello World 的程度。不要仅仅满足于能够实现功能即可,还需要保证代码的准确性以及高运行效
正式进入代码阶段
链表的基本操作
链表的基本操作,基本可以按照下图中从上到下的流程依次来掌握。
基本可以概括为增、删、查找。其中,添加和删除头结点、尾节点的时间复杂度为O(1),查找操作以及向链表中间位置插入节点的时间复杂度则为O(n)。
工欲善其事必先利其器
正所谓巧妇难为无米之炊在开始实现以上几个操作之前,我们必须先实现一个链表的节点Node。有了节点之后,才能展开后续的一些列操作。
实现代码:
class LinkedList
{
Node head; // 链表中的头节点
Node tail; // 链表中的尾节点
/*
* 节点类,包含数据域data
* 和指向下一个节点的指针next
*/
class Node {
int data;
Node next;
Node(int d) {
data = d;
next = null;
}
}
}为了操作方便,我们一般会在一个链表中保存一个head引用和一个tail引用,分别用来保存链表的头节点和尾节点。这种机制通常被叫做哨兵机制。当初始化链表LinkList时,头节点和尾节点都为null,也就是一个空链表。
有了节点之后,就可以来看一下链表基本操作的具体实现了。
先从查找节点开始
searchNode、nodeAtPosition
因为后续的插入和删除操作会用到这里的代码,所以将查找操作放到前面来讲。查找操作分为两种:searchNode和nodeAtPosition,见名知意一个是根据value查找,另一个是根据下标index查找。
searchNode: 查找指定value的节点
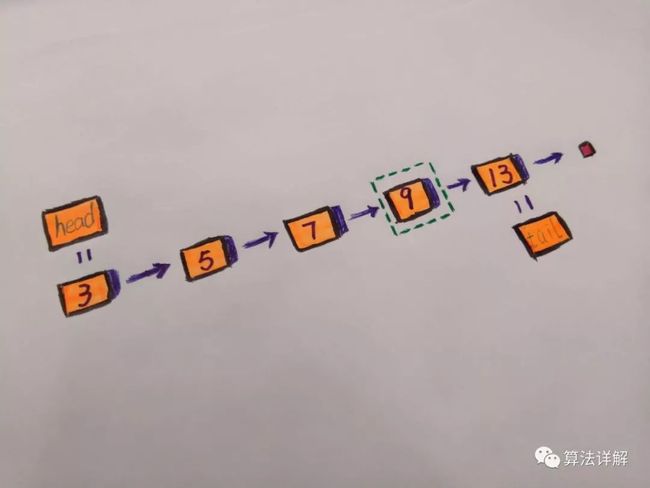
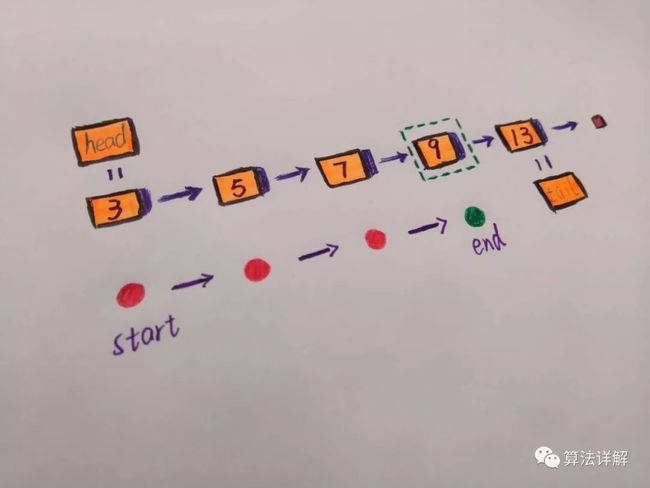
比如要在下列链表中,查找是否含有value等于9的节点,如果找到就返回,否则返回null。
我们只要从head节点3开始,依次判断所遍历到的节点value是否等于9,如果不是就继续遍历节点next所指向的下一个节点。
也就是说,查找操作需要遍历链表中的每一个节点进行判断,直到找到相应节点或者遍历到尾结点tail为止。因此时间复杂度为O(n)。
实现代码如下:
/*
* 查找指定元素,找到了返回节点Node,找不到返回null
*/
public Node searchNode(int value){
Node current = head; // 从头结点head开始遍历
while(current != null){ // 只有尾节点tail的next指向null
if(value == current.data){
return current; // 找到节点并返回
}else{
current = current.next; // 继续遍历下一个节点
}
}
return null; // 遍历整个链表也没有找到,返回null
}
nodeAtPosition: 查找指定位置index的节点
根据下标查找相对简单一些,只要定义一个循环次数就是index的 while语句 即可,直接贴出代码
1 private Node nodeAtPosition(int index) {
2 verify (index >= 0); // 伪代码,检验输入index是否有效
3
4 Node result = head; // 从头节点head开始,取index次next引用的节点
5
6 while (index > 0) {
7 result = result.next;
8 index--;
9 }
10
11 return result;
12 }
接下来插入节点
addLast、addHead、addNode
addLast
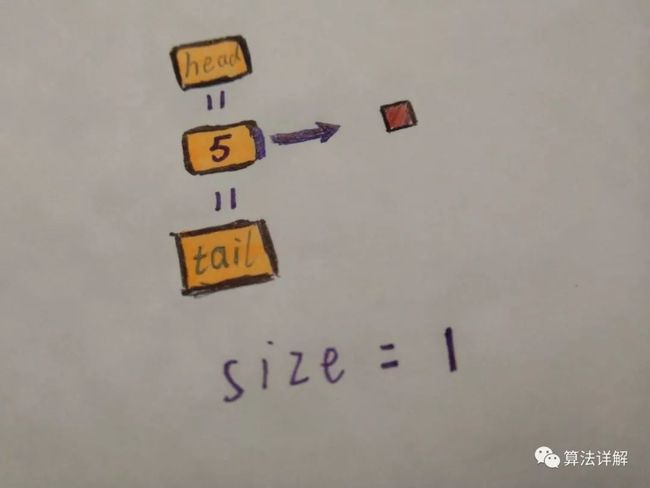
我们调用 addLast(int value) 方法,向链表尾部插入一个元素5。向链表中插入元素时,我们需要判断链表是否为空链表。
1. 如果此时的链表是一个空链表,只需要将被插入元素同时赋值给head和tail节点即可。此时被插入的元素即是头结点,也是尾结点。
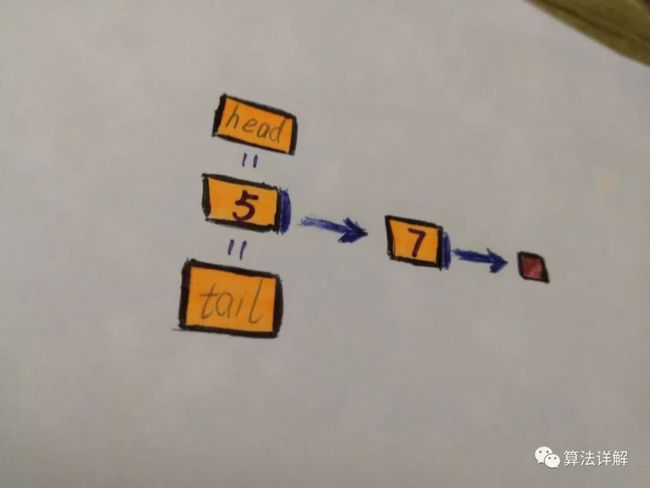
2. 如果链表不为空,这种情况头节点head不需要做任何修改,所有的操作都发生在链表的尾部:
2.1 先将尾节点5的next指针指向被插入元素
2.2 然后重新将被插入元素赋值给尾结点tail即可。
此时的尾节点变为被插入节点
同样的操作,依次插入9、13之后的链表如下: 将元素9、13插入到链表中
具体实现代码如下:
void addLast(int value) {
Node newNode = new Node(value);
if (head == null) { // 空链表
head = tail = newNode;
} else { // 非空链表
// 将当前尾节点的next指针指向被插入元素
tail.next = newNode;
}
tail = newNode; // 重新将被插入元素赋值给tail节点
size++;
}
addHead
我们调用 addHead(int value) 方法,向链表头部插入一个元素。这个操作甚至比 addLast 更加简单,为什么这么说呢,先看下代码:
1void addHead(String value) {
2 Node newNode = new Node(value);
3
4 newNode.next = head; // 将head赋值给新插入节点的next指针
5 head = newNode; // 重新将被插入节点赋值给head引用
6 size++;
7}
可以看出,在addHead方法中,甚至都不需要判断链表是否为空链表。因为即使head是null,第4行代码无非就是将被插入节点newNode的next指针指向一个空值null罢了,然后在第5行代码中会重新给head赋值。因此addHead方法不需要判断操作,因为代码很简单,并且同addLast类似,这里就不再贴图占用篇幅了。
addNode(int index, int value)
这是一个比较重量级的操作,意思是向链表中index位置上,插入指定vaule的节点。比如
输入:
原始链表 3->5->8->10, index = 2, value = 9
则输出
修改后链表 3->5->9->8->10
基本可以按照以下思路去实现这一操作:
从0下标开始遍历链表到 position - 1 的位置
当遍历到 position - 1 的节点(可叫做currentNode)时,根据传入的value创建节点newNode
将被插入节点newNode的next指针指向当前currentNode的next指针指向的节点
重新将当前currentNode的next指针指向newNode
1 /*
2 * linked list
3 */
4 public void addNode(int index, int value) {
5 if ((index < 0) || (index > size)) {
6 String badIndex =
7 new String ("index " + index + " must be between 0 and " + size);
8 throw new IndexOutOfBoundsException(badIndex);
9 }
10 if (index == 0) {
11 addHead (value);
12 } else {
13 addAfter (nodeAtPosition (index - 1), value);
14 }
15 size++;
16 }
注意:新手可能经常会将步骤3和步骤4的执行顺序给颠倒!导致的后果就是指针丢失
【插图--正常执行顺序和错误执行顺序】
最后删除节点
removeLast、removeHead、removeNode
链表的删除操作同添加操作基本大同小异,遵循的规律也是一样的。所以直接po出代码,就不配图了。
removeNode: 删除指定下标的节点
1/**
2 * 删除指定位置的节点,时间复杂度O(n)
3 */
4public void removeNode(int index){
5 if(index < 0 || index > size){
6 throw new IllegleStateException();
7 }
8 //删除链表中的第一个元素
9 if(index == 0){
10 removeHead();
11 }
12
13 int i=1;
14 Node preNode = head;
15 Node curNode = preNode.next;
16
17 while(curNode != null){
18 if(i == index){
19 preNode.next = curNode.next;
20 }
21 preNode = curNode;
22 curNode = curNode.next;
23 i++;
24 }
25}
removeHead: 删除头节点
1void removeHead() {
2 if (head == null) {
3 String exceptionMsg = new String ("LinkList is empty");
4 throw new IndexOutOfBoundsException(badIndex);
5 }
6 Node temp = head;
7 head = head.next;
8 tmp.next = null;
9 size--;
10}
removeLast: 删除尾节点
因为我们已经实现了删除指定下标的节点,而尾节点的下标就是size - 1,所以直接调用 removeNode(size - 1) 即可
/*
* 直接调用removeNode,所以时间复杂度也为O(n)
*/
void removeFirst() {
removeNode(size - 1);
}链表
内容小结
链表的操作无非就是添加、删除、查找操作
01
添加节点
addLast 添加尾节点,时间复杂度O(1)
addHead 添加头节点,时间复杂度O(1)
addNode 添加节点到链表指定位置,时间复杂度O(n)
02
删除结点
removeLast 删除尾节点,时间复杂度O(1)
removeHead 删除头节点,时间复杂度O(1)
removeNode 删除指定位置的节点,时间复杂度O(n)
03
查找节点
searchNode 搜索指定value的节点,时间复杂度O(n)
nodeAtPosition 搜索指定位置的节点,时间复杂度O(n)
链表操作极容易发生指针丢失
应聘者在面试时,如果遇到稍微复杂的链表操作,比如一个经典的链表题--单链表反转(我司必考题),可以尝试列举一个具体的例子,并通过画图来李理清思路,看图写代码就简单多了。
链表的操作需要考虑边界情况
针对这种情况,给应聘者的建议就是对你写出的实现代码提出以下几个问题,如果对于每个问题的回答都是肯定的,那就说明你给出的代码基本考虑到了边界情况。
如果链表为空时,代码是否能正常工作?
如果链表只包含一个结点时,代码是否能正常工作?
如果链表只包含两个结点时,代码是否能正常工作
链表的中级操作
此文主要是列举了链表的几个基本操作,但是在面试中经常会碰到一些更加复杂的链表操作,这里列举几个比较典型的操作,后续会在APP端给出实现思路以及具体实现代码。
1. 单链表反转
2. 链表的倒序打印
3. 找到倒数第k个元素
4. 检测链表是否有环
5. 两个有序链表的合并
扫描二维码, 下载App了解更多