基于CNN的人群密度图估计方法简述
人群计数的方法分为传统的视频和图像人群计数算法以及基于深度学习的人群计数算法,深度学习方法由于能够方便高效地提取高层特征而获得优越的性能是传统方法无法比拟的。
本文就使用单张人群图像,简单的介绍下近几年基于CNN进行密度图估计,从而进行人群计数的方法。
-
传统的人群计数方法
传统的人群计数方法可以分为两类,基于检测的方法和基于回归的方法。-
基于检测的方法
早期的计数方法主要是基于检测的方法,使用一个滑动窗口来检测场景中的人群,并统计人数。 基于检测的方法可以分为两类:- 基于整体的检测,训练一个分类器,利用从行人全身提取到的小波,HOG,边缘等特征检测行人。 学习的方法有SVM,boosting和随机森林等。 基于整体的方法主要适用于稀疏人群,随着人群密度的提升,人与人之间的遮挡越来越严重,这种方法就不再适用。
- 基于部分的身体的检测。 为了处理人与人的遮挡问题,主要通过检测身体的部分结构,例如头,肩膀等去统计人群的数量。这种方法比之基于整体的检测,在效果上有略微的提升。
-
基于回归的方法
论何种基于检测的方法,都很难处理人群之间严重的遮挡问题。所以,基于回归的方法逐渐被用来解决人群计数的问题。 基于回归的方法,主要思想是**学习一种特征到人群数量的映射。**该类方法主要分为两步:1. 提取场景的低级特征,例如例如前景特征,边缘特征,纹理和梯度特征;2. 学习一个回归模型,例如线性回归,岭回归或者高斯过程回归,学习一个低级特征到人群数的映射关系。 -
基于密度图的方法
基于回归的方法虽然能在一定程度上解决遮挡的问题,但是由于是使用整幅图像的特征进行回归技术,从而忽略了图像的空间信息。在2010年的Visual Geometry Group University of Oxford提出了:学习图像的局部特征和其相应的密度图之间的映射,从而在计数的过程中加入图像的空间信息。 论文地址:Learning To Count Objects in Images . 该论文最早提出使用密度图来进行计数的方法,后来很多的图像计数多数基于此方法。
-
-
基于深度学习的方法
深度学习在计算机的视觉的识别,分割,检测相比传统的方法都取得了很大的进步,人群计数也不例外,近年来的方法多数是使用深度学习的方法,利用深度学习的学历能力得到图像到其相应的人群密度图或者数量。
传统的方法通常都是输入图像的一个patch,并且通常分为两个步骤:特征的提取,回归或者分类,而基于CNN的方法则输入是一种完整的图片,并且进行end-to-end的训练。无论是使用回归或者密度图,CNN的方法都能取得较好的结果。
本文主要总结下,近几年关于使用CNN基于单幅人群图像生成密度图的方法。
MCNN (cvpr2016)
zhang等人提出了 Multi-column Convolutional Neural Network (MCNN)网络来预测人群的密度图。MCNN中有三大创新:
- 提出了MCNN网络,能够处理任意大小的图像,并且使利用3个具有不同卷积核大小的网络来分别提取人群图像的特征,来适应人群头部大小的变化。
- 提出一种根据人头标记生成人群密度图的方法
- 构建了一个新的数据集 Shanghaitech ,包含1198张图像约有330000个人头标记数据。
作者认为,人群计数存在着以下的困难:
- 前景的分割,现有的计数方法通常需要前景分割,而前景分割是很困难的。使用MCNN网络则不需要进行前景分割,输入任意的人群图像,通过CNN网络直接估计其密度图。
- 密集人群存在严重的遮挡
- 人群图像中人的尺度存在着较大的差异就需要融合多种图像的特征来估计人群的数量,这些特征人工则很难设计。
为了应对以上问题,作者提出了MCNN网络,使用3个不同尺度的卷积网络提取图像的多尺度特征,并使用 1 × 1 1 \times 1 1×1的卷积核将多尺度的特征融合到一起。 其网络结构如下:
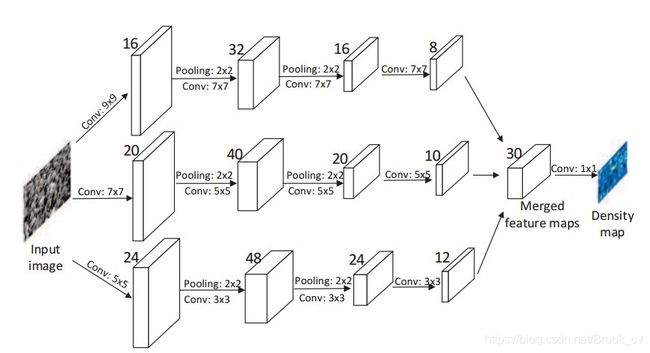
这类利用多个网络的模型具有较多的参数,计算量大,无法进行实时的人群计数预测。而且多阵列的网络并不能如所描述的一般,提取不同的尺度的人头特征。
密度图的生成
人群计数的数据集,通常是标记了人头的位置,就需要根据人头位置的数据来生成相应的人群密度图。 MCNN种提出了一种自适应卷积核的方法,来生成相应的密度图。
在由标记生成密度图的过程,首先将每个人头对应的位置设置为1,然后对该图像进行高斯卷积。
代码如下:
img = cv2.imread(path)
density = np.zeros((img.shape[0],img.shape[1]))
for i inr range(0,len(gt)):
if int(gt[i][1]) < img.shape[0] and int(gt[i][0]) < img.shape[1]:
density[int(gt[i][1]),int(gt[i][0])] = 1
density = cv2.GaussianBlur(density,(5,5))
这种构建的密度图是假设人头相对于图像平面是独立存在的,事实上,由于透视畸变的村子,不同位置人头对应着不同大小的像素区域。 因此,要想生成精确的人群密度图像,就要考虑单应性引起的畸变,但是畸变参数是不容易得到的。故,作者假设每个头部周围的人群分布比较均匀,那么头部与其最近的k个邻居之间的平均距离,给出了一个合理的几何失真估计(由透视效果引起)。而且作者在拥挤的场景中,头部的大小通常与相邻两个人中心的距离有关。 作为一种折衷,对于那些拥挤场景的密度图,建议根据每个人与其邻居的平均距离来自适应地确定每个人的扩展参数,也就是高斯卷积核的方差。
也是就,其为每个人头位置根据其与周围相邻的人头的距离来构建卷积的方差,然后将所有人头点卷积后的结果累加到一起,就是最终生成的密度图。具体代码如下:
gt_count = np.count_nonzero(gt)
if gt_count == 0:
return density
# FInd out the K nearest neighbours using a KDTree
pts = np.array(list(zip(np.nonzero(gt)[1].ravel(), np.nonzero(gt)[0].ravel())))
leafsize = 2048
# build kdtree
tree = scipy.spatial.KDTree(pts.copy(), leafsize=leafsize)
# query kdtree
distances, locations = tree.query(pts, k=4)
for i, pt in enumerate(pts):
pt2d = np.zeros(gt.shape, dtype=np.float32)
pt2d[pt[1],pt[0]] = 1.
if gt_count > 1:
sigma = (distances[i][1]+distances[i][2]+distances[i][3])*0.1
else:
sigma = np.average(np.array(gt.shape))/2./2. #case: 1 point
#Convolve with the gaussian filter
density += scipy.ndimage.filters.gaussian_filter(pt2d, sigma, mode='constant')
CP-CNN (cvpr 2017)
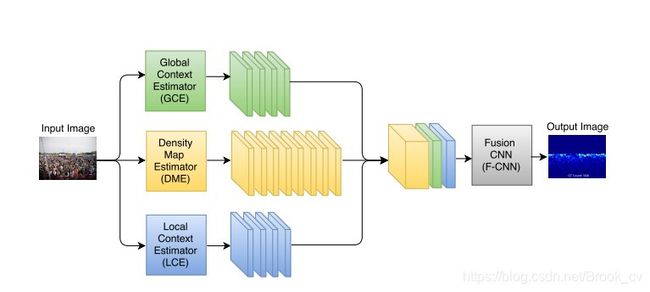
CP-CNN( Generating High-Quality Crowd Density Maps using Contextual Pyramid CNNs) 使用图像的全局和局部特征信息生成估计人群图像的密度图。
绿色子网络表示对整张输入图像做特征提取并分类(类别为作者分好的密度等级,即当前输入图像属于哪个密度等级),并将分类结果张成一个与密度特征具有相同高和宽的图像(全局上下文);蓝色子网络对原图中割出的patch做同样的操作,得到局部上下文。最终将全局和局部上下文特征与原图产生的密度图(黄色部分)在通道维度拼接(concate)。该方法的初衷是为了考虑一幅图像中人群的全局密度和局部密度信息,最后对整个特征做约束,使得网络对任何一张图像都自适应的学到相应密度等级的特征。
CSRNet (cvpr 2018)
CSRnet网络模型主要分为前端和后端网络,采用剔除了全连接层的VGG-16作为CSRnet的前端网络,提取图像的特征,输出密度图的大小为原始输入图像的1/8。采用空洞卷积神经网络作为后端网络,在保持分辨率的同时扩大感知域, 生成高质量的人群分布密度图。
采用剔除了全连接层的VGG-16网络,并且采用3×3的卷积核。研究表明,对于相同大小的感知域,卷积核越小,卷积层数越多的模型要优于那些有着更大卷积核且卷积层数较少的模型。为了平衡准确性和资源开销,这里的VGG-16网络采用10层卷积层和3层池化层的组合。后端网络采用六层空洞卷积层,空洞率相同。最后采用一层1×1的普通卷积层输出结果,其网络结构如下:

CSRNet的主要思路是,使用预训练的VGG进行特征提取,后面再使用空洞卷积,在扩大感受野的同时,生成人群的密度图。
ic-CNN (ECCV 2018)
Iterative Crowd Counting,其采取的思路是首先生成低分辨率的密度图,然后进一步的细化来生成高分辨率的密度图。该网络结构由两个CNN分支组成,一个分支用来生成低分辨率的密度图,另一个使用生成的低分辨率的密度图以及提取的特征图的基础上,生成高分辨率的密度图。其网络结构如下:
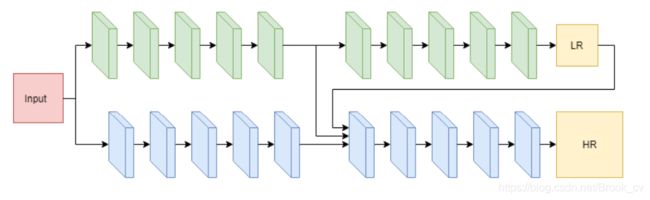
该网络的输入是一个三元组 D = { ( X 1 , Y 1 , Z 1 ) , … , ( X n , Y n , Z n ) } \mathcal{D}=\left\{\left(X_{1}, Y_{1}, Z_{1}\right), \ldots,\left(X_{n}, Y_{n}, Z_{n}\right)\right\} D={(X1,Y1,Z1),…,(Xn,Yn,Zn)},其中 X i X_i Xi是输入的图像, Y i Y_i Yi是和原图像相同分辨率的密度图, Z i Z_i Zi则是低分辨率的密度图。
对于生成低分辨率密度图的分支LR-CNN,其输入是 X i X_i Xi,则可以用如下公式表示
Z ^ i = f l ( X i ; θ l ) \hat{Z}_{i}=f_{l}\left(X_{i} ; \theta_{l}\right) Z^i=fl(Xi;θl)
其中, Z ^ i \hat{Z}_{i} Z^i是生成的低分辨率的密度图。
对于生成高分辨率的分支HR-CNN,其输入则是 X i , Z i ^ X_i,\hat{Z_i} Xi,Zi^,其表示如下
Y ^ i = f h ( X i , Z ^ i ; θ l , θ h ) \hat{Y}_{i}=f_{h}\left(X_{i}, \hat{Z}_{i} ; \theta_{l}, \theta_{h}\right) Y^i=fh(Xi,Z^i;θl,θh)
其损失函数为
L ( θ l , θ h ) = 1 n ∑ i = 1 n ( λ l L ( Z ^ i , Z i ) + λ h L ( Y ^ i , Y i ) ) \mathcal{L}\left(\theta_{l}, \theta_{h}\right)=\frac{1}{n} \sum_{i=1}^{n}\left(\lambda_{l} L\left(\hat{Z}_{i}, Z_{i}\right)+\lambda_{h} L\left(\hat{Y}_{i}, Y_{i}\right)\right) L(θl,θh)=n1i=1∑n(λlL(Z^i,Zi)+λhL(Y^i,Yi))
使用HR-CNN输出的高分辨率的密度图作为最终的输出结果。其表现如下

SANet(ECCV 2018)
Scale Aggregation Network for Accurate and Efficient Crowd Counting,该方法同样考虑要提取每个图像的多个尺度的人头信息,但并不采取类似MCNN的多阵列网络结构,其使用了类似于Inception架构的模块,在每个卷积层都同时使用不同大小的卷积核,最后通过反卷积得到最终的密度图。
简单来说,就是使用一系列的Inception结构提取不同尺度的特征,再使用反卷积(Transposed CONV)生成高分辨率的密度图,其网络结构如下:
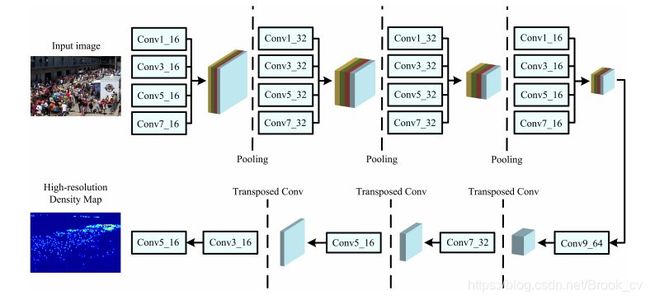
Summary
简单的梳理了下2016年到2018年出现的一些基于CNN生成人群密度图的方法。 可以看出,生成人群密度图的难点仍然是:人头的重叠以及人头尺度的变化。 这两个困难有时候有可以看作是一个:人头尺度变小了,其看着就重叠到了一起。 所以目前主流的方法,仍然是提取多尺度的人头特征信息,当然也有ic-CNN这样的从低分辨率密度图细化到高分辨率的密度图。