【洛谷P1228】地毯填补问题【分治】【递归】【DFS】

题目大意：

题目链接：https://www.luogu.org/problemnew/show/P1228
用L型地毯铺满一个边长为 2k 2 k 的正方形，要求有一个特殊点不能铺且其他每个点都仅被一个地毯铺到的方案。
L型地毯为以下几种图案：

---

思路：

首先考虑 2×2 2 × 2 的情况。假设这个特殊点在 (1,1) ( 1 , 1 ) ，那么很明显正确的填法是这样的：

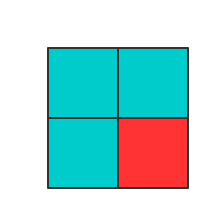
那么接下来就要扩大到 4×4 4 × 4 了：

这时候，另外三个 2×2 2 × 2 的未上色格子就没有特殊点了，也就没法像一开始的 2×2 2 × 2 的格子做。那么可不可以给每个 2×2 2 × 2 的格子都增加一个特殊点呢？
答案很明显是可以的。只要在四个 2×2 2 × 2 的格子的正中间旁边的3个白色格子都填上同一种颜色，然后再分别处理三个 2×2 2 × 2 的格子就可以！

那么再分别处理三个 2×2 2 × 2 格子，得到

那么同理，当我们扩充到 8×8 8 × 8 的格子时候，也用同样的方法，现将中间点旁边的白点标记为特殊点。

然后同理。。。

那么就可以推出 210 2 10 大小的答案啦！

那么，如果要我们求 210 2 10 大小的答案，那么就首先找到它的中点，判断特殊点再那边，然后就往那边递归，就变成 29×29 2 9 × 2 9 了，之后一直递归下去直到变成 2×2 2 × 2 ，然后就像上面说的一样慢慢染色输出啦！

---

代码：

#include 
using namespace std;

int n,k,a[1201][1201];

void dfs(int x1,int y1,int x2,int y2,int X,int Y)
{
    if (x2-x1==1&&y2-y1==1)  //变成了2*2
    {
        if (X==x1&&Y==y1) printf("%d %d 1\n",x2,y2);
        if (X==x1&&Y==y2) printf("%d %d 2\n",x2,y1);
        if (X==x2&&Y==y1) printf("%d %d 3\n",x1,y2);
        if (X==x2&&Y==y2) printf("%d %d 4\n",x1,y1);
        return;
    }
    int x=(x2-x1+1)/2+x1-1;
    int y=(y2-y1+1)/2+y1-1;  //取出中点
    //接下来就是分治特殊点的位置，往那个方向搜索。
    if (X<=x&&Y<=y)  
    {
        dfs(x1,y1,x,y,X,Y);
        printf("%d %d 1\n",x+1,y+1);
        dfs(x+1,y1,x2,y,x+1,y);
        dfs(x+1,y+1,x2,y2,x+1,y+1);
        dfs(x1,y+1,x,y2,x,y+1);
    }
    if (X<=x&&Y>y) 
    {
        dfs(x1,y+1,x,y2,X,Y);
        printf("%d %d 2\n",x+1,y);
        dfs(x1,y1,x,y,x,y);
        dfs(x+1,y1,x2,y,x+1,y);
        dfs(x+1,y+1,x2,y2,x+1,y+1);
    }
    if (X>x&&Y<=y) 
    {
        dfs(x+1,y1,x2,y,X,Y);
        printf("%d %d 3\n",x,y+1);
        dfs(x+1,y+1,x2,y2,x+1,y+1);
        dfs(x1,y1,x,y,x,y);
        dfs(x1,y+1,x,y2,x,y+1);
    }
    if (X>x&&Y>y) 
    {
        dfs(x+1,y+1,x2,y2,X,Y);
        printf("%d %d 4\n",x,y);
        dfs(x1,y1,x,y,x,y);
        dfs(x1,y+1,x,y2,x,y+1);
        dfs(x+1,y1,x2,y,x+1,y);
    }
}

int main()
{
    int x,y;
    scanf("%d%d%d",&k,&x,&y);
    n=1;
    for (int i=1;i<=k;i++)
     n*=2;  //我就不用(1<1,1,n,n,x,y);
    return 0;
}