POJ3984&&HDU1180,广度搜索BFS？acm新手成长之路

POJ3984和HDU1180：《广度搜索（BFS）》迷宫问题

广度搜索和深度搜索（dfs）

先普及一波广度搜索和深度搜索的概念：

如图，我们要从上往下搜索树的每个节点，用深度搜索，每个节点搜到的先后顺序如图，如果用广度搜索，搜到的节点顺序将是1-2-7-8-3-6-9-12-4-5-10-11。深度搜索优先搜索到最深层，到尽头在往分支搜索，一般使用递归或者栈来实现。广度搜索则是一层一层的搜到底。一般用队列来实现。
今天两题都是用bfs来做（这几天都有多校的比赛没时间找dfs的题目，抱歉了各位），先看POJ3984

---

poj3984

定义一个二维数组：
int maze[5][5] = {
0, 1, 0, 0, 0,
0, 1, 0, 1, 0,
0, 0, 0, 0, 0,
0, 1, 1, 1, 0,
0, 0, 0, 1, 0,
};
它表示一个迷宫，其中的1表示墙壁，0表示可以走的路，只能横着走或竖着走，不能斜着走，要求编程序找出从左上角到右下角的最短路线
Input
一个5 × 5的二维数组，表示一个迷宫。数据保证有唯一解。
Output
左上角到右下角的最短路径，格式如样例所示。
Sample Input
0 1 0 0 0
0 1 0 1 0
0 0 0 0 0
0 1 1 1 0
0 0 0 1 0
Sample Output
(0, 0)
(1, 0)
(2, 0)
(2, 1)
(2, 2)
(2, 3)
(2, 4)
(3, 4)
(4, 4)
题意都清楚了,这题明显的bfs模板题，只是记录路线有点麻烦，可以将每个格子标号，在记录走到这个格子的前一格子的编号即可。

#include
#include
#include
#include   //队列
using namespace std;
int map1[5][5];
      //迷宫地图
int vis[5][5];
     //判断格子是否走过，避免重复，0表示没走过
struct Node
{
    int x,y;
    int pre;    //记录前一个格子的编号，方便输出。
}node[30];
int to[2][4]={1,0,-1,0,0,1,0,-1};
bool judge(int x,int y)
 //判断格子是否为可到达
{
    if(x>=0&&y>=0&&x<5&&y<5&&map1[x][y]==0)
        return 1;
    else
        return 0;
}
queue Q;
void bfs()
{    node[0].pre=-1;
     //起点的前一个格子标记为-1
    Q.push(node[0]);
    Node a;
    vis[0][0]=1;
    int x1,y1,num;
    while(!Q.empty())
    {
        a=Q.front();
        Q.pop();
     //删除队列头元素
        for(int i=0;i<4;i++)
 //每个格子有4个方向可以移动
        {
            x1=a.x+to[0][i];
            y1=a.y+to[1][i];
            num=x1*5+y1;
   //将横纵坐标转化为格子编号，方便记录
            if(judge(x1,y1)&&!vis[x1][y1])
            {   vis[x1][y1]=1;
         //避免重复
               node[num].pre=a.x*5+a.y;  //记录前一个格子编号
               if(x1==4&&y1==4)
                  return ;
 //到达终点
               Q.push(node[num]);
            }
        }
    }
}
void print(int x)//递归输出
{
    int t=node[x].pre;
    if(t==-1)

        {
            printf("(%d, %d)\n",node[0].x,node[0].y);
           return ;
      }
    else
    {
        print(t);
    }
        printf("(%d, %d)\n",node[x].x,node[x].y);
}
int main()
{
    int cnt=0;
    memset(vis,0,sizeof(vis));
    for(int i=0;i<5;i++)
    {
        for(int j=0;j<5;j++)
        {
            scanf("%d",&map1[i][j]);
            node[cnt].x=i;node[cnt++].y=j;
        }
    }
    bfs();
    print(24);
    return 0;
}

HDU1180这题也和上题一样是模板题，只是这题多了个梯子的判断

Hogwarts正式开学以后,Harry发现在Hogwarts里,某些楼梯并不是静止不动的，相反,他们每隔一分钟就变动一次方向.
比如下面的例子里,一开始楼梯在竖直方向,一分钟以后它移动到了水平方向,再过一分钟它又回到了竖直方向.Harry发现对他来说很难找到能使得他最快到达目的地的路线,这时Ron(Harry最好的朋友)告诉Harry正好有一个魔法道具可以帮助他寻找这样的路线,而那个魔法道具上的咒语,正是由你纂写的.
Input
测试数据有多组，每组的表述如下：
第一行有两个数,M和N,接下来是一个M行N列的地图,’*’表示障碍物,’.’表示走廊,’|’或者’-‘表示一个楼梯,并且标明了它在一开始时所处的位置:’|’表示的楼梯在最开始是竖直方向,’-‘表示的楼梯在一开始是水平方向.地图中还有一个’S’是起点,’T’是目标,0<=M,N<=20,地图中不会出现两个相连的梯子.Harry每秒只能停留在’.’或’S’和’T’所标记的格子内.
Output
只有一行,包含一个数T,表示到达目标的最短时间.
注意:Harry只能每次走到相邻的格子而不能斜走,每移动一次恰好为一分钟,并且H子而不能斜走,每移动一次恰好为一分钟,并且Harry登上楼梯并经过楼梯到达对面的整个过程只需要一分钟,Harry从来不在楼梯上停留.并且每次楼梯都恰好在Harry移动完毕以后才改变方向.
Sample Input
5 5
**..T
* * .*.
..|..
..*..
S….
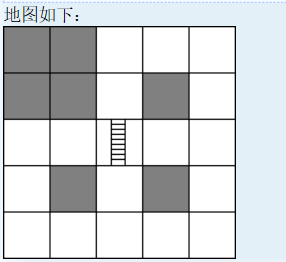（字符间没空格）

//HDU1180;
#include
#include
#include
using namespace std;
const int INF=100000;
int n,m;
struct Node
{
    int x,y;
    int step;
   //走到该格子需要的步数
}node[401];
char map1[21][21];
queue Q;
bool judge(int x,int y)  //判断格子是否能进入
{
    if(x>=0&&y>=0&&x'*')
        return 1;
    else
        return 0;
}
int to[2][4]={1,0,-1,0,0,1,0,-1};
void bfs()
{
    Node a;
    while(!Q.empty())
    {
        a=Q.front();
        Q.pop();
        for(int i=0;i<4;i++)
        {
            int x1=a.x+to[0][i];
            int y1=a.y+to[1][i];
            int num=x1*m+y1;
            if(judge(x1,y1))
            {
                if((map1[x1][y1]=='.'||map1[x1][y1]=='T')&&node[num].step>a.step+1)
//这里判断>a.step+1才更新表示当前路线比之前的快，若是慢就没必要更了
                {   node[num].step=a.step+1;
                    Q.push(node[num]);
                }
                else if(map1[x1][y1]=='|'&&a.step%2==0)/*模2等于0表示梯子方向和初始方向一致*/
                {     num+=(to[0][i]*m+to[1][i]);
  //不会在梯子上停留，所以再向前走一格
                    if((i==0||i==2)&&node[num].step>a.step+1)
                    {
                        node[num].step=a.step+1;
                        Q.push(node[num]);
                    }
                    else if((i==1||i==3)&&node[num].step>a.step+2)
                    {
                        node[num].step=a.step+2;
                        Q.push(node[num]);
                    }
                }
                else if(map1[x1][y1]=='|'&&a.step%2==1)
                {      num+=(to[0][i]*m+to[1][i]);
                     if((i==0||i==2)&&node[num].step>a.step+2)
                    {
                        node[num].step=a.step+2;
                        Q.push(node[num]);
                    }
                    else if((i==1||i==3)&&node[num].step>a.step+1)
                    {
                        node[num].step=a.step+1;
                        Q.push(node[num]);
                    }
                }
                else if(map1[x1][y1]=='-'&&a.step%2==1)
                {    num+=(to[0][i]*m+to[1][i]);
                    if((i==0||i==2)&&node[num].step>a.step+1)
                    {
                        node[num].step=a.step+1;
                        Q.push(node[num]);
                    }
                    else if((i==1||i==3)&&node[num].step>a.step+2)
                    {
                        node[num].step=a.step+2;
                        Q.push(node[num]);
                    }
                }
                else if(map1[x1][y1]=='-'&&a.step%2==0)
                {       num+=(to[0][i]*m+to[1][i]);
                     if((i==0||i==2)&&node[num].step>a.step+2)
                    {
                        node[num].step=a.step+2;
                        Q.push(node[num]);
                    }
                    else if((i==1||i==3)&&node[num].step>a.step+1)
                    {
                        node[num].step=a.step+1;
                        Q.push(node[num]);
                    }
                }
            }
        }
    }
}
int main()
{
    while(~scanf("%d%d",&n,&m))
    {    int cnt=0;
         int S,T;
        for(int i=0;ifor(int j=0;j>map1[i][j];
                node[cnt].x=i;node[cnt].y=j;
                 node[cnt++].step=INF;  //初始化为最大值
                 if(map1[i][j]=='S')
                    {
                        S=cnt-1;
    //记录起点的位置
                        node[S].step=0;
                    }
                if(map1[i][j]=='T')
                {
                    T=cnt-1;
    //终点位置
                }
            }
        }
        Q.push(node[S]);
        bfs();
        printf("%d\n",node[T].step);
    }return 0;
}

今天的题是不是so easy？我的前几篇博客会先写寒假训练的基础内容，也是方便各位新手学习（现在学的太难我也做不出，要不也不会多校的时候才A两题）。这些博客见证了我acm新手的成长之路，大家有什么好的算法解法可以留言相互学习。