今天也大致学了下KM算法,用于求二分图匹配的最佳匹配。
何为最佳?我们能用匈牙利算法对二分图进行最大匹配,但匹配的方式不唯一,如果我们假设每条边有权值,那么一定会存在一个最大权值的匹配情况,但对于KM算法的话这个情况有点特殊,这个匹配情况是要在完全匹配(就是各个点都能一一对应另一个点)情况下的前提。
自然,KM算法跟匈牙利算法有相似之处。
其算法步骤如下:
1.用邻接矩阵(或其他方法也行啦)来储存图,注意:如果只是想求最大权值匹配而不要求是完全匹配的话,请把各个不相连的边的权值设置为0。
2.运用贪心算法初始化标杆。
3.运用匈牙利算法找到完备匹配。
4.如果找不到,则通过修改标杆,增加一些边。
5.重复3,4的步骤,直到完全匹配时可结束。
一言不合地冒出了个标杆??标杆是什么???
在解释这个问题之前,我们先来假设一个很简单的情况,用我们人类伟大的智能思维去思考思考。
我们可以思索思索
二分图最佳匹配还是二分图匹配,所以跟和匈牙利算法思路差不多
二分图是特殊的网络流,最佳匹配相当于求最大(小)费用最大流,所以FF方法也能实现
所以我们可以把这匈牙利算法和FF方法结合起来
FF方法里面,我们每次是找最长(短)路进行通流
所以二分图匹配里面我们也找最大边进行连边!
但是遇到某个点被匹配了两次怎么办?
那就用匈牙利算法进行更改匹配!
这就是KM算法的思路了:尽量找最大的边进行连边,如果不能则换一条较大的。
所以,根据KM算法的思路,我们一开始要对边权值最大的进行连线,那问题就来了,我们如何让计算机知道该点对应的权值最大的边是哪一条?或许我们可以通过某种方式
记录边的另一端点,但是呢,后面还要涉及改边,又要记录边权值总和,而这个记录端点方法似乎有点麻烦,于是KM采用了一种十分巧妙的办法(也是KM算法思想的精髓):
添加标杆(顶标)
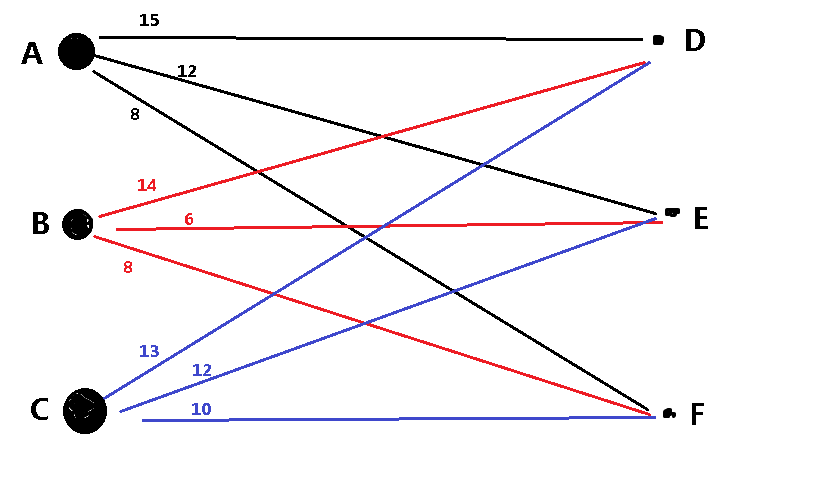
是怎样子呢?我们对左边每个点Xi和右边每个点Yi添加标杆Cx和Cy。
其中我们要满足Cx+Cy>=w[x][y](w[x][y]即为点Xi、Yi之间的边权值)
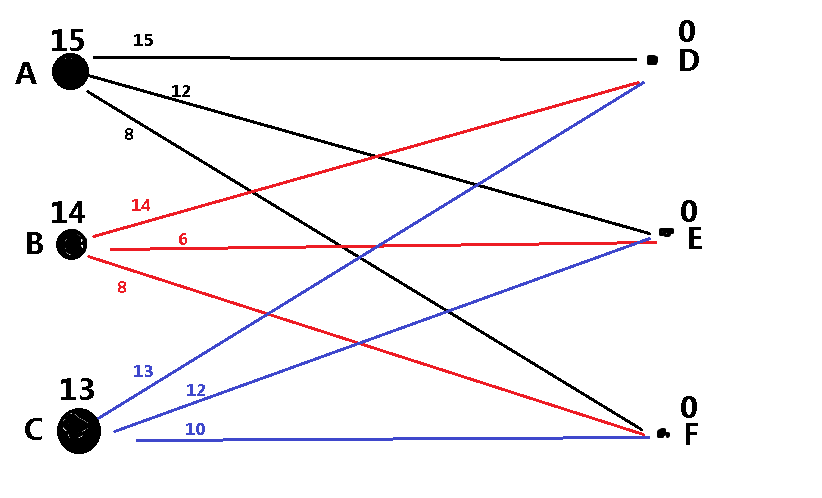
对于一开始的初始化,我们对于每个点分别进行如下操作
Cx=max(w[x][y]);
Cy=0;
然后,我们可以进行连边,即采用匈牙利算法,只是在判断两点之间是否有连线的条件下,因为我们要将最大边进行连线,所以原来判断是否有边的条件w[x][y]==0换成了
Cx+Cy==w[x][y]
此时,有一个新的名词——相等子图。
因为我们通过了巧妙的处理让计算机自动连接边权最大的边,换句话说,其他边计算机就不会连了,也就“不存在”这个图中,但我们可以随时加上这些“不存在”图中的边。此时这个图可以认为是原图的子图,并且是等效。
这样,计算机在枚举右边的点的时候,满足以上条件,就能够知道这条边是我们要连的最大的边,就能进行连边了。
于是乎我们连了AD。
接下来就尴尬了,计算机接下来要连B点的BD,但是D点已经和A点连了,怎么办呢???
根据匈牙利算法,我们做的是将A点与其他点进行连线,但此时的子图里“不存在”与A点相连的其他边,怎么办呢??
为此,我们就需要加上这些边!
很明显,我们添边,自然要加上不在子图中边权最大的边,也就是和子图里这个边权值差最小的边。
于是,我们再一度引入了一变量d,d=min{Cx[i]+Cy[j]-w[i][j]}
其中,在这个题目里Cx[i]指的是A的标杆,Cy[j]是除D点(即已连点)以外的点的标杆。
随后,对于原先存在于子图的边AD,我们将A的标杆Cx[i]减去d,D的标杆Cy[d]加上d。
这样,这就保证了原先存在AD边保留在了子图中,并且把不在子图的最大权值的与A点相连的边AE添加到了子图。
因为计算机判断一条边是否在该子图的条件是其两端的顶点的标杆满足
Cx+Cy==w[x][y]
对于原先的边,我们对左端点的标杆减去了d,对右端点的标杆加上了d,所以最终的结果还是不变,仍然是w[x][y]。
对于我们要添加的边,我们对于左端点减去了d,即Cx[i]=Cx[i]-d;为方便表示我们把更改后的的Cx[i]视为Cz[i],即Cz[i]=Cx[i]-d;
对于右端点,我们并没有对其进行操作。那这条我们要添加边的两端点的标号是否满足Cz[i]+Cy[j]=w[i][j]?
因为Cz[i]=Cx[i]-d;d=Cx[i]+Cy[j]-w[i][j];
我们把d代入左式可得Cz[i]=Cx[i]-(Cx[i]+Cy[j]-w[i][j]);
化简得Cz[i]+Cy[j]=w[i][j]。
满足了要求!即添加了新的边。
值得注意的是,这里我们只是对于一条边操作,当我们添加了几条边,要进行如上操作时,要保证原先存在的边不消失,那么我们就要先求出了d,然后
对于每个连边的左端点(记作集合S)的每个点的标号减去了d之后,然后连边的右端点(记作T)加上d,这样就保证了原先的边不消失啦~
实际上这就是一直在寻找着增广路,通过不断修改标杆进行添边实现。
接下来就继续着匈牙利算法,直到完全匹配完为止。
该算法的正确性就在于 它每次都选择最大的边进行连边
至此,我们再回顾KM算法的步骤:
1.用邻接矩阵(或其他方法也行啦)来储存图。
2.运用贪心算法初始化标杆。
3.运用匈牙利算法找到完备匹配。
4.如果找不到,则通过修改标杆,增加一些边。
5.重复3,4的步骤,直到完全匹配时可结束。
是不是清楚了许多??
因为二分图是网络流的一种特殊情况,在网络流里我们是通过不断的SPFA找到费用最大(小)的路径进行通流,跟这个有点类似。
如果我们要求边权值最小的匹配呢???
我们可以把边权值取负值,得出结果后再取相反数就可以了。
至于为什么,正负大小相反了嘛~
至此,这大概是我个人的一点点理解了,希望对您有所帮助。
若有不当之处还请大家指出QwQ。
1 #include2 #include 3 #include 4 using namespace std; 5 const int qwq=0x7fffffff; 6 int w[1000][1000]; //w数组记录边权值 7 int line[1000],usex[1000],usey[1000],cx[1000],cy[1000]; //line数组记录右边端点所连的左端点, usex,usey数组记录是否曾访问过,也是判断是否在增广路上,cx,cy数组就是记录点的顶标 8 int n,ans,m; //n左m右 9 bool find(int x){ 10 usex[x]=1; 11 for (int i=1;i<=m;i++){ 12 if ((usey[i]==0)&&(cx[x]+cy[i]==w[x][i])){ //如果这个点未访问过并且它是子图里面的边 13 usey[i]=1; 14 if ((line[i]==0)||find(line[i])){ //如果这个点未匹配或者匹配点能更改 15 line[i]=x; 16 return true; 17 } 18 } 19 } 20 return false; 21 } 22 int km(){ 23 for (int i=1;i<=n;i++){ //分别对左边点依次匹配 24 while (true){ 25 int d=qwq; 26 memset(usex,0,sizeof(usex)); 27 memset(usey,0,sizeof(usey)); 28 if (find(i)) break; //直到成功匹配才换下一个点匹配 29 for (int j=1;j<=n;j++) 30 if (usex[j]) 31 for (int k=1;k<=m;k++) 32 if (!usey[k]) d=min(d,cx[j]+cy[k]-w[j][k]); //计算d值 33 if (d==qwq) return -1; 34 for (int j=1;j<=n;j++) 35 if (usex[j]) cx[j]-=d; 36 for (int j=1;j<=m;j++) 37 if (usey[j]) cy[j]+=d; //添加新边 38 } 39 } 40 ans=0; 41 for (int i=1;i<=m;i++) 42 ans+=w[line[i]][i]; 43 return ans; 44 } 45 int main(){ 46 while (~scanf("%d%d",&n,&m)){ 47 memset(cy,0,sizeof(cy)); 48 memset(w,0,sizeof(w)); 49 memset(cx,0,sizeof(cx)); 50 for (int i=1;i<=n;i++){ 51 int d=0; 52 for (int j=1;j<=n;j++){ 53 scanf("%d",&w[i][j]); 54 d=max(d,w[i][j]); //此处顺便初始化左边点的顶标 55 } 56 cx[i]=d; 57 } 58 memset(line,0,sizeof(line)); 59 printf("%d\n",km()); 60 } 61 return 0; 62 }