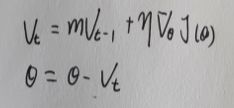常用优化器(Adam SGD)算法
文章目录
- 概览
- SGD (Stochastic gradient descent)
- Momentum
- NAG(Nesterov accelerated gradient)
- AdaGrad
- RMSPro Adadelta
- Adam
概览
梯度下降算法
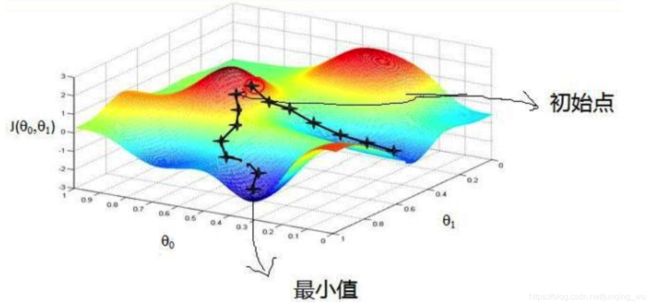
关于梯度下降算法的直观理解,我们以一个人下山为例。比如刚开始的初始位置是在红色的山顶位置,那么现在的问题是该如何达到蓝色的山底呢?按照梯度下降算法的思想,它将按如下操作达到最低点:
- 明确自己现在所处的位置
- 找到相对于该位置而言下降最快的方向
- 沿着第二步找到的方向走一小步,到达一个新的位置,此时的位置比原来低
- 回到第一步
- 终止于最低点
按照以上5步,最终达到最低点,这就是梯度下降的完整流程。当然你可能会说,上图不是有不同的路径吗?是的,因为上图并不是标准的凸函数,往往不能找到最小值,只能找到局部极小值。所以你可以用不同的初始位置进行梯度下降,来寻找更小的极小值点,因为网络的目标函数往往不满足 严格的凸函数,所以可能从不同的初始值出发可能达到不同的局部最小值。
pytorch 提供的优化器接口
from .adadelta import Adadelta # noqa: F401
from .adagrad import Adagrad # noqa: F401
from .adam import Adam # noqa: F401
from .adamw import AdamW # noqa: F401
from .sparse_adam import SparseAdam # noqa: F401
from .adamax import Adamax # noqa: F401
from .asgd import ASGD # noqa: F401
from .sgd import SGD # noqa: F401
from .rprop import Rprop # noqa: F401
from .rmsprop import RMSprop # noqa: F401
from .lbfgs import LBFGS # noqa: F401
SGD (Stochastic gradient descent)
θ = θ − ∇ θ J ( θ ) \theta = \theta - \nabla_\theta J(\theta) θ=θ−∇θJ(θ)
-
批量梯度下降
针对整个数据集进行梯度的计算,可以求得全局最优解,但是当数据集比较大时,计算开销大,计算速度慢 -
随机梯度下降
每次只通过随机选取的数据对 ( x i , y i ) (x^i,y^i) (xi,yi)来求梯度,计算速度快,但是由于每次只选取一个样本对进行更新,很可能导致 损失函数震荡的现象,不易收敛。 -
小批量梯度下降
每次选择一个批量(btach)样本进行更新,折中方案 1. 减少了参数更新的变化,这可以带来更加稳定的收敛。2:可以充分利用矩阵优化,最终计算更加高效。
Momentum
通过使用动量,减缓目标函数的震荡,加快收敛速度。
pytorch实现
# dampening一般为0
for p in group['params']:
if p.grad is None:
continue
d_p = p.grad.data
if weight_decay != 0:
d_p.add_(weight_decay, p.data)
if momentum != 0:
param_state = self.state[p]
if 'momentum_buffer' not in param_state:
buf = param_state['momentum_buffer'] = torch.clone(d_p).detach()
else:
buf = param_state['momentum_buffer']
buf.mul_(momentum).add_(1 - dampening, d_p)
if nesterov: # NAG
d_p = d_p.add(momentum, buf)
else:
d_p = buf
p.data.add_(-group['lr'], d_p)
V t = V t − 1 + ∇ θ J ( θ ) V_t = V_{t-1} + \nabla_\theta J(\theta) Vt=Vt−1+∇θJ(θ)
θ = θ − V t \theta = \theta-V_t θ=θ−Vt
NAG(Nesterov accelerated gradient)
该优化器相对于Momentum,唯一不同的是计算反向梯度的时机。
V t = V t − 1 + ∇ θ J ( θ + V t − 1 ) V_t = V_{t-1} + \nabla_\theta J(\theta+V_{t-1}) Vt=Vt−1+∇θJ(θ+Vt−1)
θ = θ − V t \theta = \theta-V_t θ=θ−Vt
Momentum 在当前位置上求梯度,但是NAG是在上个动量的方向上前进一小步,然后再计算梯度,相当于:
上次是往前走了10米,这次我先往前走上2米,然后再来观察下一步怎么走。可以认为是分两步更新了theta。
AdaGrad
Adagrad优化算法是一种自适应优化算法,针对高频特征更新步长较小,而低频特征更新较大。因此该算法适合应用在特征稀疏的场景。
先前的算法对每一次参数更新都是采用同一个学习率,而adagrad算法每一步采用不同的学习率进行更新,衰减系数是 历史所有梯度的平方和。我们计算梯度的公式如下:


state['sum'].addcmul_(1, grad, grad) # s = s + grad * grad
std = state['sum'].sqrt().add_(group['eps']) # d = sqrt( s + eps)
p.data.addcdiv_(-clr, grad, std) # p = p - lr/d * grad
Adagrad算法的主要优点是它避免了手动调整学习率的麻烦,大部分的实现都采用默认值0.01。
分析
- 从AdaGrad算法中可以看出,随着算法不断迭代,r会越来越大,整体的学习率会越来越小。所以,一般来说AdaGrad算法一开始是激励收敛,到了后面就慢慢变成惩罚收敛,速度越来越慢。
- 在SGD中,随着梯度的增大,我们的学习步长应该是增大的。但是在AdaGrad中,随着梯度g的增大,我们的r也在逐渐的增大,且在梯度更新时r在分母上,也就是整个学习率是减少的,这是为什么呢?
这是因为随着更新次数的增大,我们希望学习率越来越慢。因为我们认为在学习率的最初阶段,我们距离损失函数最优解还很远,随着更新次数的增加,越来越接近最优解,所以学习率也随之变慢。 - 经验上已经发现,对于训练深度神经网络模型而言,从训练开始时积累梯度平方会导致有效学习率过早和过量的减小。AdaGrade在某些深度学习模型上效果不错,但不是全部。
- dagrad算法主要的缺点在于,其分母梯度平方的累加和。因为每次加入的都是一个正数,随着训练的进行,学习率将会变得无限小,此时算法将不能进行参数的迭代更新。
RMSPro Adadelta
这两者都是基于Adagrad的基础进行改进,主要是通过不同的方法 解决adagrad导致的学习趋近于零**(学习率消失)**,网络不学习的问题 。
通过约束历史梯度累加来替代累加所有历史梯度平方。这里通过在历史梯度上添加衰减因子,并通过迭代的方式来对当前的梯度进行计算,最终距离较远的梯度对当前的影响较小,而距离当前时刻较近的梯度对当前梯度的计算影响较大,公式
S t = m ∗ S t − 1 + ( 1 − m ) ∗ g r a d ∗ g r a d S_t = m*S_{t-1} + (1-m)*grad*grad St=m∗St−1+(1−m)∗grad∗grad
随着网络更新,之前保留的梯度对 当前的下降方向 影响已经很小了,所以将累加的 梯度和 乘以 衰减系数, 权重梯度基于最近量级的均值为每一个参数适应性地保留学习率。
square_avg.mul_(alpha).addcmul_(1 - alpha, grad, grad) # s = a*s + (1-a)*g*g
Adam
Adam 则是 结合了 自适应学习策略Adagrad 和 Momentum的更新思想
Adam 算法和传统的随机梯度下降不同。随机梯度下降保持单一的学习率(即 alpha)更新所有的权重,学习率在训练过程中并不会改变。而 Adam 通过计算梯度的一阶矩估计和二阶矩估计而为不同的参数设计独立的自适应性学习率 Adam 算法的提出者描述其为两种随机梯度下降扩展式的优点集合,即:
-
适应性梯度算法(AdaGrad)为每一个参数保留一个学习率以提升在稀疏梯度(即自然语言和计算机视觉问题)上的性能。
-
均方根传播(RMSProp)基于权重梯度最近量级的均值为每一个参数适应性地保留学习率。这意味着算法在非稳态和在线问题上有很有优秀的性能。
Adam 算法同时获得了 AdaGrad 和 RMSProp 算法的优点。Adam 不仅如 RMSProp 算法那样基于一阶矩均值计算适应性参数学习率,它同时还充分利用了梯度的二阶矩均值(即有偏方差/uncentered variance)。具体来说,算法计算了梯度的指数移动均值(exponential moving average),超参数 beta1 和 beta2 控制了这些移动均值的衰减率。移动均值的初始值和 beta1、beta2 值接近于 1(推荐值),因此矩估计的偏差接近于 0。该偏差通过首先计算带偏差的估计而后计算偏差修正后的估计而得到提升。
存在的问题:
- 可能不收敛
对于SGD和AdaGrad来说,其学习率都是单调的,即单调递减,因此,这两类算法会使得学习率不断递减,最终收敛到0,模型也得以收敛。
但是对于Adam和AdaDelta,其学习率二阶估计是取固定时间窗口内的动量累加,随着窗口和数据的变化,二阶动量可能会产生的波动,从而引起学习率震荡,导致模型无法收敛;
- 可能错过全局最优解
另外一篇是 ImproVing Generalization Performance by Switching from Adam to SGD,进行了实验验证。他们CIFAR-10数据集上进行测试,Adam的收敛速度比SGD要快,但最终收敛的结果并没有SGD好。他们进一步实验发现,主要是后期Adam的学习率太低,影响了有效的收敛。他们试着对Adam的学习率的下界进行控制,发现效果好了很多。
于是他们提出了一个用来改进Adam的方法:前期用Adam,享受Adam快速收敛的优势;后期切换到SGD,慢慢寻找最优解。这一方法以前也被研究者们用到,不过主要是根据经验来选择切换的时机和切换后的学习率。这篇文章把这一切换过程傻瓜化,给出了切换SGD的时机选择方法,以及学习率的计算方法,效果看起来也不错。
参考资料:
都9102年了,别再用Adam + L2 regularization了
优化方法总结以及Adam存在的问题