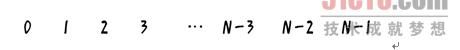约瑟夫环（数学高效率解法，很详细）



5.5.4 用数学方法解约瑟夫环（1）

原文copy:http://book.51cto.com/art/201403/433941.htm

5.5.4  用数学方法解约瑟夫环（1）

上面编写的解约瑟夫环的程序模拟了整个报数的过程，程序运行时间还可以接受，很快就可以出计算结果。可是，当参与的总人数N及出列值M非常大时，其运算速度就慢下来。例如，当N的值有上百万，M的值为几万时，到最后虽然只剩2个人，也需要循环几万次（M的数量）才能确定2个人中下一个出列的序号。显然，在这个程序的执行过程中，很多步骤都是进行重复无用的循环。

那么，能不能设计出更有效率的程序呢？

办法当然有。其中，在约瑟夫环中，只是需要求出最后的一个出列者最初的序号，而不必要去模拟整个报数的过程。因此，为了追求效率，可以考虑从数学角度进行推算，找出规律然后再编写程序即可。

为了讨论方便，先根据原意将问题用数学语言进行描述。

问题：将编号为0～（N–1）这N个人进行圆形排列，按顺时针从0开始报数，报到M–1的人退出圆形队列，剩下的人继续从0开始报数，不断重复。求最后出列者最初在圆形队列中的编号。

下面首先列出0～（N–1）这N个人的原始编号如下：

根据前面曾经推导的过程可知，第一个出列人的编号一定是（M–1）%n。例如，在41个人中，若报到3的人出列，则第一个出列人的编号一定是（3–1）%41=2，注意这里的编号是从0开始的，因此编号2实际对应以1为起点中的编号3。根据前面的描述，m的前一个元素（M–1）已经出列，则出列1人后的列表如下：

根据规则，当有人出列之后，下一个位置的人又从0开始报数，则以上列表可调整为以下形式（即以M位置开始，N–1之后再接上0、1、2……，形成环状）：

按上面排列的顺序重新进行编号，可得到下面的对应关系：
 

即，将出列1人后的数据重新组织成了0～（N–2）共N–1个人的列表，继续求n–1个参与人员，按报数到M–1即出列，求解最后一个出列者最初在圆形队列中的编号。

看出什么规律没有？对了，通过一次处理，将问题的规模缩小了。即，对于N个人报数的问题，可以分解为先求解（N–1）个人报数的子问题；而对于（N–1）个人报数的子问题，又可分解为先求[（N–1）–1]人个报数的子问题，……。

问题中的规模最小时是什么情况？就是只有1个人时（N=1），报数到（M–1）的人出列，这时最后出列的是谁？当然只有编号为0这个人。因此，可设有以下函数：
 

那么，当N=2，报数到（M–1）的人出列，最后出列的人是谁？应该是只有一个人报数时得到的最后出列的序号加上M，因为报到M-1的人已出列，只有2个人，则另一个出列的就是最后出列者，可用公式表示为以下形式：
 

通过上面的算式计算时，F(2)的结果可能会超过N值（人数的总数）。例如，设N=2，M=3（即2个人，报数到2时就出列），则按上式计算得到的值是：
 

一共只有2人参与，编号为3的人显然没有。怎么办？由于是环状报数，因此当两个人报完数之后，又从编号为0的人开始接着报数。根据这个原理，即可对求得的值与总人数N进行模运算，即：
 

5.5.4  用数学方法解约瑟夫环（2）

即，N=2，M=3（即有2个人，报数到3–1的人出列）时，循环报数最后一个出列的人的编号为1（编号从0开始）。我们来推算一下，如下所示，当编号为0、1的两个人循环报数时，编号为0的人报的数为0和2，当报到2（M–1）时，编号0出列，最后剩下编号为1的人，所以编号为1的人最后出列。

根据上面的推导过程，可以很容易推导出，当N=3时的公式：

同理，也可以推导出参与人数为N时，最后出列人员编号的公式：

其实，这就是一个递推公式，公式包含以下两个式子：

有了这个递推公式，再来设计程序就很简单了，可以用递归的方法来设计程序，具体代码如下：
 

#include <stdio.h>
int main(void)
{
    int n,m,i,s=0;
    printf ("输入参与人数N和出列位置M的值 = ");
    scanf("%d%d",&n,&m);

    printf ("最后出列的人最初位置是 %d\n",josephus(n,m));
    getch();
    return 0 ;
}

int josephus(int n,int m)
{
    if(n==1)
        return 0;
    else
        return (josephus(n-1,m)+m)%n;
}

在以上代码中，定义了一个递归函数josephus()，然后在主函数中调用这个函数进行   运算。

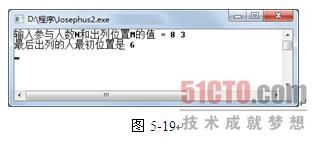
编译执行以上程序，输入N和M的值，可以很快得到最后出列人的编号，输入N=8，M=3，得到的结果如图5-19所示（注意编号是从0开始）。
 

使用递归函数会占用计算机较多的内存，当递归层次太深时可能导致程序不能执行，因此，也可以将程序直接编写为以下的递推形式：
 

#include <stdio.h>
int main(void)
{
    int n,m,i,s=0;
    printf ("输入参与人数N和出列位置M的值 = ");
    scanf("%d%d",&n,&m);
    for (i=2; i<=n; i++)
        s=(s+m)%i;
    printf ("最后出列的人最初位置是 %d\n",s);
    getch();
    return 0 ;
}

这段代码执行的结果与递归程序执行结果完全相同。

可以看出，经过一些数学推导，最后总结出规律简化程序，将几十行的代码缩减到几行。更主要的是，程序执行的效率得到大大的提升，省去了很多重复的循环，既使求解的N和M值很大，也不会成为问题