主动学习(Active Learning)系列介绍(三)搜索假设空间(Searching Through the Hypothesis Space)
本文介绍主动学习Active Learning中的第二种query selection framework —— 搜索假设空间Searching Through the Hypothesis Space,其主要思想是利用缩小版本空间找到需要的query instance。
文章目录
- 版本空间 The Version Space
- 通过搜索版本空间解释不确定度采样 Uncertainty Sampling as Version Space Search
- 通过分歧查询 Query by Disagreement
- 通过委员会查询 Query by Committee
- 讨论 Discussion
- 参考文献
版本空间 The Version Space
关于假设空间和版本空间的概念,可详见【机器学习基础】假设空间 VS 版本空间
在机器学习术语中,我们通常用假设hypothesis表示一个计算模型,它既可以解释训练数据,也可以对新的示例进行预测,通常用 H H H来表示。版本空间 V V V则是假设空间的子集 V ⊂ H V\subset H V⊂H,用来表示假设空间中满足训练样本的假设集合。
随着我们获得越来越多的有标记数据labeled data,版本空间的大小 ∣ V ∣ |V| ∣V∣会越来越小,因此,主动学习active learning的目标可以认为获取新的query instance来快速减少版本空间大小 ∣ V ∣ |V| ∣V∣。
我们继续以“探索外星植被”为例,详见主动学习(Active Learning)系列介绍(一)基本概念及应用场景。

黄色区域表示该问题的版本空间。一开始时,只有未标记数据unlabeled data,因此版本空间 == 假设空间。在每一轮寻找query instance的过程中,我们都希望尽可能地缩小版本空间大小 ∣ V ∣ |V| ∣V∣,因此我们每次选择的query instance都是位于版本空间中间位置的instance。
通过以上的这个例子,我们简单解释了“通过假设空间搜索”的思想,主要就是尽可能地通过选择query instance来缩减版本空间。
通过搜索版本空间解释不确定度采样 Uncertainty Sampling as Version Space Search
在介绍本章的具体算法之前,我们先讲解一下前面提及的不确定度采样Uncertainty Sampling和本文介绍的搜索版本空间Version Space Search之间的关系。
从概念定义来看,搜索版本空间的目标是尽量消除不合理的假设,而不确定度采样则是通过一种假设(a single hypothesis)来选择一个最不确定的instance,两者仿佛完全不同。然而,在某些特定条件下,不确定度采样的目标也是缩小版本空间大小!
这是因为两者都利用到了最大间隔max-margin的思想。我们拿SVM算法作为分类器举例说明。
假设我们的数据是 K K K维的特征空间,有趣的是,特征空间feature space与假设空间hypothesis space之间存在着某种二元映射关系。详见下图:
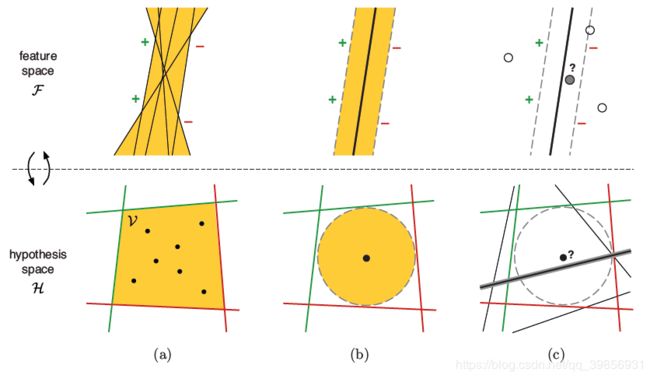
上面一行表示特征空间,下面一行表示假设空间。
图( a )中,特征空间中的点对应假设空间的线。图中黄颜色的区域仍然代表版本空间。
图( b )中,上图的黑色实线就代表SVM算法中的超平面,其与支持向量的间隔margin最大,对应到下图,就是在版本空间中找出一个黑点,其到各个边界的距离最大。
图( c )中,上图选择一个距离决策边界最近的点(最不确定)对应在下图中将版本空间平分的那一条线。
用这个例子我们可以看到在某些算法中,不确定度采样可以理解为搜索版本空间的思想。
然而,不确定度采样uncertainty sampling仍然有一些问题。首先,只有版本空间对称时才能被平分,当版本空间不对称甚至不规则时有些算法无法使用。为解决这个问题Tong and Koller (2000)提出一种基于决策理论的SVM算法,不需要再考虑最大化间隔的问题。目前不确定度采样uncertainty sampling在多种方法中都比较适用
通过分歧查询 Query by Disagreement
基于以上介绍的搜索假设空间的思想,Cohn等人在1994年提出了Query by Disagreement(QBD)算法。QBD算法是基于stream-based selective sampling的场景,即对于每一个instance,判断其是要query还是丢弃。QBD算法的伪代码如下:

对于一个示例instance,若在版本空间 V V V中有任意两个假设 h 1 ( x ) h_1(x) h1(x)和 h 2 ( x ) h_2(x) h2(x)对其的预测结果不一致,则认为该示例为query instance,需要拿去送标,这就是query by disagreement的思想。我们可以想象有一块区域,在这区域中的示例都会被认为disagree,这个区域叫分歧区域a region of disagreementDIS( V V V)。
然而版本空间可能是无限的,上述算法的时间消耗较大,可采用如下的简化方法:

重新定义两个假设 h 1 h_1 h1和 h 2 h_2 h2,对示例instance进行判断,若结果不同,则作为query instance;否则将instance丢弃。然而,如果模型的训练过程是十分耗时的,那么此方法反而会让算法变得很慢。
另一种思路是参考假设hypothesis的普遍性“generality”。参考下图:

黄色区域仍然是版本空间。其中最靠近正例的假设是“most general hypothesis”,最靠近负例的假设是“most specific hypothesis”,分别为 h S ( x ) h_S(x) hS(x)和 h G ( x ) h_G(x) hG(x),对于一个示例instance,我们只要判断若 h S ( x ) ≠ h_S(x)\neq hS(x)= h G ( x ) h_G(x) hG(x),则该示例为query instance。此方法称为SG-based QBD approach。
下图是分为使用random sampling, uncertainty sampling, SG-based QBD approach三种方法进行模型预测的情况,分别使用20, 40, 60, 80, 100个示例进行训练,可见SG-based QBD approach效果最好。
通过委员会查询 Query by Committee
通过分歧查询Query by Disagreement有以下两个问题:
- 使用了版本空间 V V V中的所有假设(或者两个极端的假设 h S ( x ) h_S(x) hS(x)和 h G ( x ) h_G(x) hG(x)),有时这是十分麻烦的。当数据中有噪声时,版本空间 V V V甚至很难定义。
- 之前讨论的是
stream-based selective sampling的场景,我们也想在pool-based sampling场景中找到最具价值的示例。
基于这两个问题,提出了query by committee(QBC)的方法,其主要思想就是将若干个假设hypothesis组成一个committee,再利用committee去判断新的示例instance。
query by committee(QBC)主要包含以下两个问题:
- 如何选出组成committee的hypothesis
- 如何利用committee对instance进行判断
针对问题一,可以用贝叶斯的方法计算后验概率 P ( θ ∣ L ) P(\theta|L) P(θ∣L),以及隐马尔可夫模型。同时利用集成学习的思想:bagging,boosting等方法也可以用于选择hypothesis。
针对问题二,主要有以下方法选择query instance:
- 使用KL散度(KL divergence)的方法,公式如下:

利用vote entropy方法和KL散度方法选择query instance时有一点不同:

图( a )中,每个hypothesis都是uncertain的,因此他们集成在一起时committee为uncertain。
图( b )中,每个hypothesis都有一个比较确定的值,联合在一起却是uncertain的。
这是两者最大的不同,同时KL散度更符合disagreement的思想。
在实际测试中,我们分别使用entropy-based uncertainty sampling, soft vote entropy, KL divergence三种方法进行判断query instance,如下图所示。在热力图中颜色越深,则该instance作为query instance的概率越高。

图( a )是初始的训练集数据。
图( b )是利用entropy-based uncertainty sampling,可见其较为简单,对绝大部分比较自信,只会query图中狭窄的一小部分。
图( c )是利用soft vote entropy,形成一个“Y”字型。
图( d )是利用KL divergence时,形成一个长条形。
同时,QBC也可用于回归任务,如下图所示:

每次迭代过程选择方差最大的instance作为query instance,则可将回归模型逐步趋近于目标函数target function。
讨论 Discussion
总结一下以上的内容,我们本章主要工作就是选择query instance来尽可能多地消除错误的假设,从而缩小版本空间。
利用 I ( Y ; V ) I(Y;V) I(Y;V)表示类别 Y Y Y和版本空间 V V V之间的交互信息mutual information。
我们要寻找的是最大的 I ( Y ; V ) I(Y;V) I(Y;V),此时可以考虑著名的信息学理论等式:

从某种程度来说,寻找最大的交互信息mutual information就是disagreement-based方法的本质,然而entropy-based uncertainty sampling却没有考虑假设空间,因此判断有时会不准确。
现在,让我们再回到“探索外星植被”的任务!如下图所示:

现在有两种植被,一种是红色的,一种是灰色的。
植被A还是植被B都可以将版本空间平分,这时选择A还是B就成了一个难题。
在这种情况下,我们还需要考虑数据本身的分布。比如灰色植被数目比较多,那我们可能会优先灰色植被A。
在接下里的章节中,我们会通过直接最小化分类误差来解决以上这个问题。
参考文献
Active Learning, B Settles, 2012.


