2016 Multi-University Training Contest 9题解报告

此文章可以使用目录功能哟↑(点击上方[+])

倒数第2场多校,经历5个小时只出了一题,也是蛮心塞的...

链接→2016 Multi-University Training Contest 9

 Problem 1012 Less Time, More profit

Accept: 0    Submit: 0
Time Limit: 2000/1000 MS (Java/Others)    Memory Limit : 65536/65536 K (Java/Others)

 Problem Description

The city planners plan to build N plants in the city which has M shops.

Each shop needs products from some plants to make profit of proi units.

Building ith plant needs investment of payi units and it takes ti days.

Two or more plants can be built simultaneously, so that the time for building multiple plants is maximum of their periods(ti).

You should make a plan to make profit of at least L units in the shortest period.

 Input

First line contains T, a number of test cases.

For each test case, there are three integers N, M, L described above.

And there are N lines and each line contains two integers payi, ti(1<= i <= N).

Last there are M lines and for each line, first integer is proi, and there is an integer k and next k integers are index of plants which can produce material to make profit for the shop.

1 <= T <= 30

1 <= N, M <= 200

1≤L,ti≤1000000000

1≤payi,proi≤30000

 Output

For each test case, first line contains a line “Case #x: t p”, x is the number of the case, t is the shortest period and p is maximum profit in t hours. You should minimize t first and then maximize p.

If this plan is impossible, you should print “Case #x: impossible”

 Sample Input

2

1 1 2
1 5
3 1 1

1 1 3
1 5
3 1 1

 Sample Output

Case #1: 5 2
Case #2: impossible

 Problem Idea

解题思路:

【题意】
比赛的时候,这题提问的人还是蛮多的,所以我好好讲一下该题的题意

有n个工厂,m个商店,建设第i个工厂需要花费payi的钱和ti的时间,多个工厂可以同时建设,即花费时间取最大的ti

第i个商店在指定的k个工厂都建完之后可以一次性获得proi的利润

也就是说k个工厂任何一个没有建完的情况下,该商店都不会获得利润

问最少需要多少时间,获得的总利润不少于L

在满足最少时间的情况下,求最大化的利润

【类型】
二分+网络流(最大权闭合图)

【分析】
很尴尬的,比赛的时候贪心水过了,还不小心误导了一批小伙伴,在此,我表示抱歉

首先,此题的变量太多了一些,比如我们不知道要建设哪些工厂,相对应的就不知道哪些商店能够获利,而且还不知道最少需要多少时间

所以,我们要做的第一步是先固定一些变量,就比如工厂建设工期t

故我们采取二分时间t,判断该时间下是否可以找到最大利润>=L

那如何判断是否有最大利润>=L呢?

在解决这个问题之前,我们先来了解一下,何为最大权闭合图

定义一个有向图G=(V,E)的闭合图(closure)是该有向图的一个点集,且该点集的所有出边都还指向该点集,即闭合图内的任意点的任意后继也一定在闭合图中。

更形式化地说,闭合图是这样的一个点集V'∈V,满足对于∀u∈V'引出的∀∈E,必有v∈V'成立。

还有一种等价定义为:满足对于∀∈E,若有u∈V'成立,必有v∈V'成立

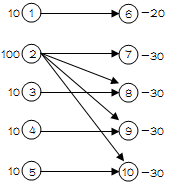
就如上图而言,该图的闭合图(含空集)有:∅,{1,6},{6},{2,7,8,9,10},{7},{3,8},{8},{4,9},{9},{5,10},{10}等等

这个"等等"是因为闭合图相互组合也是闭合图,比如{1,3,6,8}

而{2,7}不是闭合图,因为2除7以外的其他后继(8,9,10)不在该闭合图内

另外,最大权闭合图的含义就是点权之和最大的闭合图,上图最大权闭合图为{2,3,4,5,7,8,9,10},点权之和为10(100+10+10+10-30-30-30-30)

讲清楚最大权闭合图之后,我们来看看,此题和最大权闭合图有什么关系

在许多实际应用中,给出的有向图常常是一个有向无环图(DAG),闭合图的性质恰好反映了事件间的必要条件的关系:一个事件的发生,它所需要的所有前提也都要发生,而此题中的这种关系体现在何处呢?

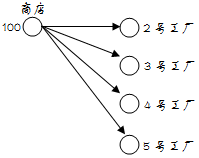
例如100 4 2 3 4 5(某商店要获利100,必须在建有2号、3号、4号、5号工厂的情况下),这整个图就构成了一个闭合图,如下所示

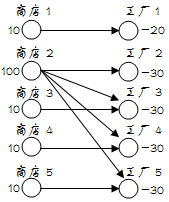
那么此题终于转化为求一个图的最大权闭合图(商店为正权点,权值为利润;工厂为负权点,权值为成本)

那么,对于下列例子,可转化为图G=(V,E)

1
5 5 10
20 1
30 1
30 1
30 1
30 1
10 1 1
100 4 2 3 4 5
10 1 3
10 1 4
10 1 5

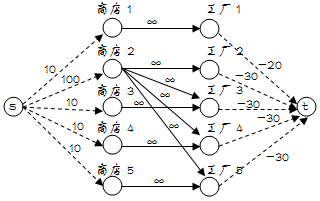
对于最大权闭合图的题目,解法为:

将原图中每条有向边替换为容量为∞的有向边

增加连接源点s到原图每个正权点v(w>0)的有向边(本题的正权点恰好为所有商店),容量为w

增加连接原图每个负权点v(w<0)到汇点t的有向边(本题的负权点恰好为所有工厂),容量为-w

∞定义为任意一个大于的整数即可,此时,最大权=正权点的总权和-最小割

而我们又知道,最小割=最大流,所以此题就成了名副其实的最大流题

而至于为什么可以用这种方法求解最大权闭合图,可以看网上证明,此处为链接->算法合集之《最小割模型在信息学竞赛中的应用》,证明在3.3节

【时间复杂度&&优化】
O(v^2elogn)

题目链接→HDU 5855 Less Time, More profit

 Source Code

/*Sherlock and Watson and Adler*/
#pragma comment(linker, "/STACK:1024000000,1024000000")
#include
#include
#include
#include
#include
#include
#include
#include

菜鸟成长记