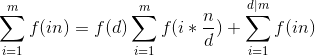Problem Description
Given a positive integers n , Mobius function μ(n) is defined as follows:
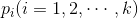are different prime numbers.
Given two integers mm, nn, please calculate 
Input
One line includes two integers m(1≤m≤2e9), n(1≤n≤1e12) .
Output
One line includes the answer .
Sample Input
2 2
Sample Output
-1
题意：已知莫比乌斯函数，求
思路：杜教筛
首先考虑 n 是否含平方因子，若 n 含有平方因子，那么根据莫比乌斯函数，每一项的 u(in) 均为 0，结果直接为 0
再考虑 n 不含平方因子，此时，每一个 n 都可以拆成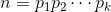 
设 
为答案
考虑 n 的一个素因子 d，由于此时的 n 不含平方因子，那么 n/d 与 d 一定是互质的，那么有： 
由于莫比乌斯函数 u(n) 是一个积性函数，且 n/d 与 d 是互质的，那么只需要考虑 d 和 i 关系，对于 [1,m] 中的数 i 和 d 只有两种可能：互质、不互质
若 i 与 d 互质，则有：
，由于 d 是素数，因此 u(d)=-1，故 
可以发现，这个式子与原式相比，多减去了一个 i 与 d 不互质的部分，因此还要加回去
考虑 [1,m] 中与 d 不互质的数，即为 [1,m] 中 d 的倍数，因此，只需要从 1 枚举到 m/d 即可，即有：
因此，最终答案即为 
即：
由于 m 十分大，因此要利用杜教筛来求前缀和，然后进行递归求值即可
值得注意的是，这类积性函数 f(x) 的 n 倍的求和都有类似的式子：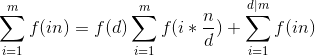
Source Program
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
