【机器学习】（十）核支持向量机SVM：make_blobs方法，hstack() 函数

SVM(核支持向量机)是可以推广到更复杂模型的扩展，可以同时用于分类(SVC)和回归(SVR)。

线性模型与非线性特征

当线性模型无法将低维空间中的类别分割，可以增添更多特征（输入特征的交互项或多项式），扩展为高维空间。x/y->x/y/z(y^2)

import matplotlib.pyplot as plt
import mglearn
from sklearn.datasets import make_blobs
from sklearn.svm import LinearSVC

x, y = make_blobs(centers=4, random_state=8) # 生成数据集和相应的标签
y = y % 2

# SVM模型
linear_svm = LinearSVC().fit(x, y)

mglearn.plots.plot_2d_separator(linear_svm, x)
mglearn.discrete_scatter(x[:,0], x[:,1], y)
plt.xlabel("Feature 0")
plt.ylabel("Feature 1")
plt.legend(['Class 0', 'Class 1'], loc=0)

make_blobs方法:sklearn.datasets.make_blobs(n_samples=100,n_features=2,centers=3, cluster_std=1.0,center_box=(-10.0,10.0),shuffle=True,random_state=None)
make_blobs函数是为聚类产生数据集，产生一个数据集和相应的标签

• n_samples:表示数据样本点个数,默认值100
• n_features:是每个样本的特征（或属性）数，也表示数据的维度，默认值是2
• centers:表示类别数（标签的种类数），默认值3
• cluster_std表示每个类别的方差，例如我们希望生成2类数据，其中一类比另一类具有更大的方差，可以将cluster_std设置为[1.0,3.0]，浮点数或者浮点数序列，默认值1.0
• center_box：中心确定之后的数据边界，默认值(-10.0, 10.0)
• shuffle ：将数据进行洗乱，默认值是True
• random_state:官网解释是随机生成器的种子，可以固定生成的数据，给定数之后，每次生成的数据集就是固定的。若不给定值，则由于随机性将导致每次运行程序所获得的的结果可能有所不同。

make_blobs函数及相应参数简介

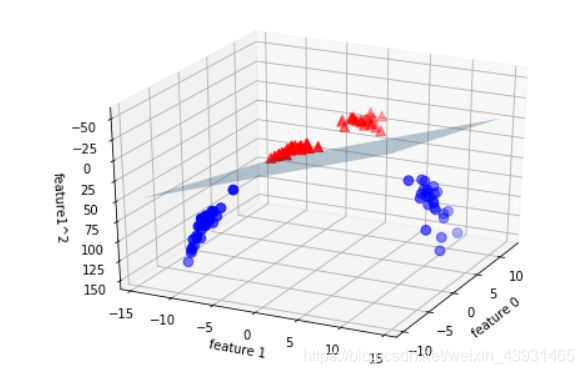
扩展特征

import numpy as np
from mpl_toolkits.mplot3d import Axes3D, axes3d

# 添加新特征（第二个特征的平方）
x_new = np.hstack([x, x[:,1:]**2]) # 水平方向堆叠数组
linear_svm_3d = LinearSVC().fit(x_new, y)
coef, intercept = linear_svm_3d.coef_.ravel(), linear_svm_3d.intercept_

# 3D可视化
figure = plt.figure()
ax = Axes3D(figure, elev=-152, azim=-26)

# 显示线性决策边界，三维空间线性模型是平面
xx = np.linspace(x_new[:,0].min()-2, x_new[:,0].max()+2.50) # 产生线性矢量
yy = np.linspace(x_new[:,1].min()-2, x_new[:,1].max()+2.50)
xx, yy = np.meshgrid(xx, yy) # 转换成矩阵
zz = (coef[0]*xx + coef[1]*yy + intercept) / -coef[2]
ax.plot_surface(xx, yy, zz, rstride=8, cstride=8, alpha=0.3)

# 先y==0,y==1
mask = y==0
ax.scatter(x_new[mask, 0], x_new[mask, 1], x_new[mask, 2], c='b', cmap=mglearn.cm2, s=60)
ax.scatter(x_new[~mask, 0], x_new[~mask, 1], x_new[~mask, 2], c='r', marker='^', cmap=mglearn.cm2, s=60)
ax.set_xlabel("feature 0")
ax.set_ylabel("feature 1")
ax.set_zlabel("feature1^2")

hstack(tup) 函数水平(按列顺序)把数组给堆叠起来，参数tup可以是元组，列表，或者numpy数组，返回结果为numpy的数组。
linspace(x1,x2,N)函数：linspace是Matlab中的均分计算指令，用于产生x1,x2之间的N点行线性的矢量。其中x1、x2、N分别为起始值、终止值、元素个数。若默认N，默认点数为100。
[X,Y]=meshgrid(x,y)函数将向量x和y定义的区域转换成矩阵X和Y，其中矩阵X的行向量是向量x的简单复制，而矩阵Y的列向量是向量y的简单复制

Numpy中stack()，hstack()，vstack()函数
Numpy中Meshgrid函数

如果看成二维平面中，这个SVM模型像个椭圆。

核技巧

向数据中添加非线性的特征的技巧就是核技巧，它直接计算扩展特征表示数据点之间的距离（内积），而不用实际对扩展进行计算。

SVM将数据映射到高维空间中两种常用方法：

• 多项式核（就像上面那样在一定阶数内计算）
• （RBF）径向基函数核/高斯核

预测新数据点

位于类别之间边界上的点叫作支持向量。
对新样本点进行预测，分类决策取决于它与每个支持向量之间的距离（由高斯核给出）以及在训练过程中学到的支持向量重要性（保存在SVC中的dual_coef_属性）

SVM参数

gamma参数：控制高斯核的宽度。gamma越小，说明高斯核半径较大，默认gamma=1/n_features。
C参数：正则化参数，限制每个点的重要性（dual_coef_）。C很小，说明模型受限（几乎线性），增大后，决策边间发生弯曲。默认C=1。
gamma和C控制的都是模型复杂度，较大的值对应更为复杂的模型，两个值相互关联，需要同时调节。

在cancer数据集应用RBF核

from sklearn.svm import SVC
from sklearn.datasets import load_breast_cancer
from sklearn.model_selection import train_test_split

cancer = load_breast_cancer() 
x_train, x_test, y_train, y_test = train_test_split(cancer.data, cancer.target, random_state=0)

svc = SVC().fit(x_train, y_train)

print(svc.score(x_train, y_train))
print(svc.score(x_test, y_test))

有点小问题，我这次测试的拟合度很好，没有样例的过拟合，都不需要预处理。

优缺点

优：在低维数据和高维数据上表现均良好。
缺：对样本个数缩放表现不好（数据量大消耗时间和内存）；预处理和调参要仔细；模型很难解释