贪心算法笔记
百度上面有对贪心算法更为详细的介绍还有详细的代码
贪心算法的作用与缺点
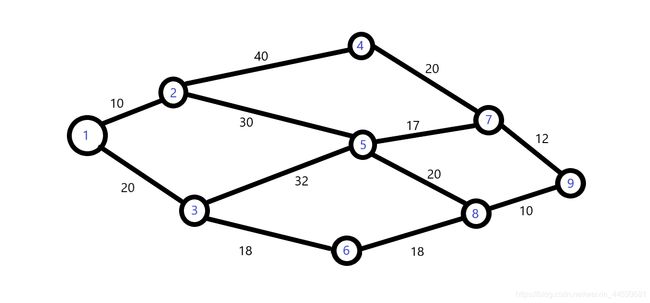
我对贪心算法的理解是每次的选择都是局部选择当中最优的选择,那么最终的整个选择是比较优的解;贪心算法的优点在于它的高效,甚至高效到可以用手动去模拟,但是缺点很明显,那就是局部最优从整体看不一定是最优解。比如在图中选择路径从1走到9,如果我们把所有路径遍历一遍再比较出最小路径是比较复杂的(在很大很大的图上这样比较时会很复杂,这个图太小了,情况数量也少,不能体现)。
贪心走法:1->2->5->7->9;
而最优路径:1->3->6->8->9.
题目
B-今年暑假不AC HDU - 2037
- 这道题所用的贪心算法不一定能求出最优解!
“今年暑假不AC?”
“是的。”
“那你干什么呢?”
“看世界杯呀,笨蛋!”
“@#$%^&*%...”
确实如此,世界杯来了,球迷的节日也来了,估计很多ACMer也会抛开电脑,奔向电视了。
作为球迷,一定想看尽量多的完整的比赛,当然,作为新时代的好青年,你一定还会看一些其它的节目,比如新闻联播(永远不要忘记关心国家大事)、非常6+7、超级女生,以及王小丫的《开心辞典》等等,假设你已经知道了所有你喜欢看的电视节目的转播时间表,你会合理安排吗?(目标是能看尽量多的完整节目)
Input
输入数据包含多个测试实例,每个测试实例的第一行只有一个整数n(n<=100),表示你喜欢看的节目的总数,然后是n行数据,每行包括两个数据Ti_s,Ti_e (1<=i<=n),分别表示第i个节目的开始和结束时间,为了简化问题,每个时间都用一个正整数表示。n=0表示输入结束,不做处理。
Output
对于每个测试实例,输出能完整看到的电视节目的个数,每个测试实例的输出占一行。
Sample Input
12
1 3
3 4
0 7
3 8
15 19
15 20
10 15
8 18
6 12
5 10
4 14
2 9
0Sample Output
5
#include
#include
#include
#include
#include
using namespace std;
const int maxn=1e3+10;
struct TV
{
int s;
int e;
}m[maxn];
bool cmp(TV a,TV b)
{
return a.e=m[i].e)
{
x++;
i+=j;
j=1;
}
else
j++;
}
printf("%d\n",x);
}
return 0;
} C-卡片游戏 HDU - 4550 此代码还没过!!哪位大佬帮看下我的代码或者留下你的代码
- 我的代码输入输出都没问题,但是一直Wrong Answer,我觉得思路应该没问题呀,下面有我的思路
小明最近宅在家里无聊,于是他发明了一种有趣的游戏,游戏道具是N张叠在一起的卡片,每张卡片上都有一个数字,数字的范围是0~9,游戏规则如下:
首先取最上方的卡片放到桌子上,然后每次取最上方的卡片,放到桌子上已有卡片序列的最右边或者最左边。当N张卡片全部都放到桌子上后,桌子上的N张卡片构成了一个数。这个数不能有前导0,也就是说最左边的卡片上的数字不能是0。游戏的目标是使这个数最小。
现在你的任务是帮小明写段程序,求出这个最小数。
Input
第一行是一个数T,表示有T组测试数据;
然后下面有T行, 每行是一个只含有0~9的字符串,表示N张叠在一起的卡片,最左边的数字表示最上方的卡片。
[Technical Specification]
T<=1000
1 <= N <= 100
Output
对于每组测试数据,请在一行内输出能得到的最小数。
Sample Input
3
565
9876543210
9876105432Sample Output
556
1234567890
1678905432我的思路:将卡片分为原本叠起来的卡片s[maxn],当前已放置在桌子上的卡片tmp[maxn];然后如果第i+1张卡片s[i]是'0',或者s[i]大于已放在桌子上的第一张卡片tmp[0],而且已放在桌子上的第一张卡片tmp[0]不为'0',就不用把第i+1张卡片s[i]放第一个,然后直接放桌子上最后的位置,否则就放在桌子上第一个!
#include
#include
#include
#include
using namespace std;
const int maxn=1e3+10;
int main()
{
int t;
scanf("%d",&t);
while(t--)
{
char s[maxn]; //代表原本叠在一起的卡片次序
scanf("%s",s);
int sl=strlen(s);
char tmp[maxn]; //当前放桌子上的卡片次序
memset(tmp,'\0',sizeof(tmp));
for(int i=0;itmp[0])&&tmp[0]!='0') //如果所取的最左边的卡片是第一张或者所取出的卡片上的数大于第一张已经放置的卡片上的数,那就直接按次序放置在最后
tmp[i]=s[i];
else //如果当前所取的最左边的卡片上的数小于已放置的第一张卡片上的数,那就把取出的卡片放置在第一张
{
for(int j=i;j>0;j--) //这是将所有卡片后移的操作
tmp[j]=tmp[j-1];
tmp[0]=s[i]; //然后将所取的卡片放在第一个
}
}
printf("%s\n",tmp);
}
return 0;
} D - 补提交卡
小Ho给自己定了一个宏伟的目标:连续100天每天坚持在hihoCoder上提交一个程序。100天过去了,小Ho查看自己的提交记录发现有N天因为贪玩忘记提交了。于是小Ho软磨硬泡、强忍着小Hi鄙视的眼神从小Hi那里要来M张"补提交卡"。每张"补提交卡"都可以补回一天的提交,将原本没有提交程序的一天变成有提交程序的一天。小Ho想知道通过利用这M张补提交卡,可以使自己的"最长连续提交天数"最多变成多少天。
Input
第一行是一个整数T(1 <= T <= 10),代表测试数据的组数。
每个测试数据第一行是2个整数N和M(0 <= N, M <= 100)。第二行包含N个整数a1, a2, ... aN(1 <= a1 < a2 < ... < aN <= 100),表示第a1, a2, ... aN天小Ho没有提交程序。
Output
对于每组数据,输出通过使用补提交卡小Ho的最长连续提交天数最多变成多少。
Sample Input
3
5 1
34 77 82 83 84
5 2
10 30 55 56 90
5 10
10 30 55 56 90
Sample Output
76
59
100
我的思路:先定义一个数组a[100]来标记这100天是否提交,tmp[ ]代表未提交的各天,由题易知,若有n(n>=m)天只有补提交卡用于相邻未提交的m天tmp[i+0],tmp[i+1],...,tmp[i+m](0<=i<=n-m)时,才可能存在最大的连续已提交天数。直接将所有n-m+1种情况全部遍历找出最大连续提交的天数即可。
#include
#include
#include
#include
#include
using namespace std;
const int maxn=1e3+10;
int main()
{
int t;
scanf("%d",&t);
while(t--)
{
int n,m,a[100],tmp[100],dayn=0,daym=0,daymaxn=0;
memset(a,1,sizeof(a));
scanf("%d%d",&n,&m);
for(int i=0;idaym)
daym=dayn;
dayn=0;
}
}
if(daym>daymaxn)
daymaxn=daym;
for(int j=0;j