衍生品定价之二:期权定价
期权定价
- 期权定价原理
- 买卖权平价关系
- 期权定价模型
- 期权定价之二叉树模型
- 期权定价之B-S-M模型
- 基础B-S-M模型
- 存续期内支付红利的B-S-M模型
- 股指期权定价
- 希腊字母
- Delta ( Δ \Delta Δ)
- Gamma ( Γ \Gamma Γ)
- Vega (v)
- Theta ( Θ \Theta Θ)
- Rho ( ρ \rho ρ)
- 波动率
期权定价原理
买卖权平价关系
买卖权平价关系,即Put-Call Parity,是指具有相同的行使价与到期日的金融工具,其卖权与买权价格间所必然存在的基本关系。如果两者不相同,则存在套利的空间。
买卖权平价关系可以描述为:在忽略市场交易成本的情况下,相同标的资产且执行价格也相同的看涨期权、看跌期权与标的资产价格之间满足如下公式关系:
C + Ke-rT = P + S
这个公式可以这么理解:
等式的左边是资产组合1,1份欧式看涨期权C和数额为Ke-rT的无风险资产;
等式的左边是资产组合2,1份条件相同的看跌期权P加上标的股票S;
其中T为到期日、r为同期限无风险收益率、K为执行价格、并假设标的资产S不进行分红。
在T时刻,资产组合1和资产组合2的价值是相同的,根据无套利定价原理,在起始时刻两个资产组合的价值也应该相同。
买卖权平价关系是期权市场最为经典且易于理解的著名等式关系。其不受制于任何期权定价模型,如BS模型,二叉树模型的影响,始终保持成立。投资者无需考虑波动率因素即可根据其来判断期权价格是否偏离合理价格,从而发现套利机会。
期权定价模型
期权定价之二叉树模型
假设股票当前时刻价格为S0,考虑以此股票为标的资产、到期日为T、执行价格为K的看涨期权的当前价格。
在到期日T时,股票的价格有两种可能:
case1:股票价格上涨到uS0(u>1), 此时期权的价值 Cu = max(0, uS0 - K) ;
case2:股票价格下跌到dS0(d<1),此时期权的价值Cd = max(0, dS0 - K) ;
结合两个case发生的概率,则该看涨期权的定价公式为:
C = e-rT * [pCu + (1-p)Cd ]
这里的概率p为“风险中性概率”,是有公式可以计算的:p = (erT - d)/(u - d)
其中 u = e σ T u=e^{\sigma\sqrt{T}} u=eσT, d=1/u。 σ \sigma σ(sigma)为历史波动率(年)。
例子:标的资产为不支付红利的股票,当前价格为每股20美元,一年后的价格或者为25美元,或者为15美元。计算对应的1年期、执行价格为18美元的欧式看涨期权的价格。设无风险年利率为8%,考虑连续复利。
解析:根据题目S0=20,uS0 = 25, dS0 = 15, 得出u=1.25, d=0.75; (这里u和d不是倒数关系了?)
Cu = max(0, 25 - 18) = 7
Cd = max(0, 15 -18) = 0
p = (erT - 0.75)/(1.25 - 0.75) = 0.66658
C = e-rT * [pCu + (1-p)Cd] = 0.92312 * 0.66658 * 7 = 4.3073
期权定价之B-S-M模型
基础B-S-M模型
B-S-M模型的思路是:在无套利机会的条件下,构造一个有股票和期权组成的无风险资产组合,这一组合的收益率必定为无风险利率r,由此得出期权价格满足的随机微分方程,进而求出期权价格。也有论文已经证明了,在极限条件下,多期的二叉树期权定价模型收敛为B-S-M模型。
B-S-M模型的六个基本假设:
- 标的资产价格服从几何布朗运动;
- 标的资产可以被自由买卖,无交易成本,允许卖空;
- 期权有效期内,无风险利率r和=预期收益率 μ \mu μ是常数,投资者可以以无风险利率无限借入或贷出资金;
- 标的资产价格是连续变动的,即不存在价格的跳跃;
- 标的资产的价格波动率 σ \sigma σ为常数;
- 市场为无套利市场;
B-S-M模型无红利资产欧式期权的价格公式为:
C = S * N(d1) - K * e-rT * N(d2)
P = K * e-rT * N(-d2) - S * N(-d1)
其实有了C的公式,根据买卖权平价关系公式 C + K * e-rT = P + S可以推导出P的公式的。
其中,S为标的资产当前价格,T为期权到期时间,K为期权执行价格;
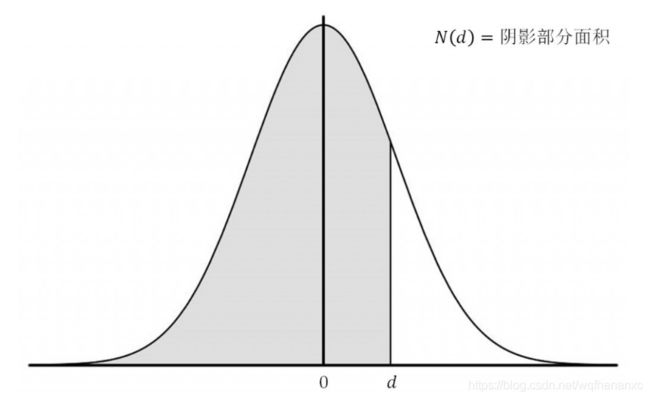
N(d)为标准正态分布小于d的概率,N(-d) = 1 - N(d);
d 1 = l n ( S / K ) + [ r + ( σ 2 / 2 ) ] T σ T d_1 =\frac{ln(S/K) + [r+(\sigma^2/2)]T}{\sigma\sqrt{T}} d1=σTln(S/K)+[r+(σ2/2)]T
d 2 = d 1 − σ T d_2 = d1 - \sigma\sqrt{T} d2=d1−σT
σ \sigma σ(sigma)为无收益标的资产的价格波动率,也即股票年收益率的标准差,用于度量资产所提供收益的不确定性。通常使用历史数据和隐含波动率来估计。
事实上,市场参与者往往从不同的角度来看期权定价问题。一般不是用所给的股票标准差按布莱克-斯科尔斯公式计算期权价格,而是将市场上的期权或权证交易价格代入权证理论价格模型,反推出来波动率的值,称之为隐含波动率。投资者可以判断实际的股票标准差是否超过了隐含波动率。如果超过了,则购买期权是一个好的选择,因为如果实际波动率高于隐含波动率,期权的公允价格就要高于观察到的价格。
另一个角度是比较到期日相同、执行价格不同的同一股票的期权。具有较高隐含波动率的期权相对贵一些,因为需要较高的标准差来调节价格。
期权价格与标的资产的价格波动率正相关。对于看涨期权来说,股价上升可以获利,股价下降时最大损失以期权费为限,两者不会抵消。因此,标的资产价格的波动率增加会使看涨期权价值增加;对于看跌期权来说,股价下降可以获利,股价上升时放弃执行,最大损失以期权费危险,两者不会抵消。因此,标的资产价格的波动率增加会使看跌期权的价值增加。
同时,期权价格与无风险收益率、期权期限也是正相关的。
例子:假设某只股票的市场价格为50,无风险利率为12%,股票的年波动率为10%,求执行价格为50、期限为1年的欧式看涨期权和看跌期权的价格。
解析: d 1 = l n ( 50 / 50 ) + [ 12 % + ( 10 % 2 / 2 ) ] ∗ 1 10 % 1 d_1 =\frac{ln(50/50) + [12\%+(10\%^2/2)]*1}{10\%\sqrt{1}} d1=10%1ln(50/50)+[12%+(10%2/2)]∗1 = 1.25
d 2 = d 1 − 10 % 1 d_2 = d1 - 10\%\sqrt{1} d2=d1−10%1 = 1.15
查累计正态分布表可得N(d1) = 0.8944, N(d2) = 0.8749
C = 50 * 0.8944 - 50 * e-12%*1 * 0.8749 = 5.92
P = C + K * e-rT - S = 5.92 + 50 * e-12%*1 - 50 = 0.27
存续期内支付红利的B-S-M模型
若存续期内,标的的资产支付红利已知,红利支付会导致资产价格下跌,看涨期权的价值也会随之下降。假设存续期内t时刻支付红利 I \Iota I,B-S-M模型带红利资产欧式期权的价格公式为:
C = (S - I \Iota I*e-rt) * N(d1*) - K * e-rT * N(d2*)
P = K * e-rT * N(-d2*) - (S - I \Iota I*e-rt) * N(-d1*)
其实就是把支付的红利折算为期初价格,从S中减去。
d 1 = l n ( ( S − I ∗ e − r t ) / K ) + [ r + ( σ 2 / 2 ) ] T σ T d_1 =\frac{ln((S - \Iota*e^{-rt})/K) + [r+(\sigma^2/2)]T}{\sigma\sqrt{T}} d1=σTln((S−I∗e−rt)/K)+[r+(σ2/2)]T
d 2 = d 1 − σ T d_2 = d1 - \sigma\sqrt{T} d2=d1−σT
股指期权定价
股指期权是以股票指数为标的物的期权产品。股票指数成分股分红的差异性以及该期权产品实行现金交割的特性,B-S-M模型定价进行修正如下:
C = ( S − ∑ i = 1 L w i I i e − r t i ) ∗ N ( d 1 ∗ ) − K ∗ e − r T ∗ N ( d 2 ∗ ) C = (S - \sum\limits_{i=1}^Lw_i\Iota_ie^{-rt_i}) * N(d_1^*) - K * e^{-rT} * N(d_2^*) C=(S−i=1∑LwiIie−rti)∗N(d1∗)−K∗e−rT∗N(d2∗)
P = K ∗ e − r T ∗ N ( − d 2 ∗ ) − ( S − ∑ i = 1 L w i I i e − r t i ) ∗ N ( − d 1 ∗ ) P = K * e^{-rT} * N(-d_2^*) - (S - \sum\limits_{i=1}^Lw_i\Iota_ie^{-rt_i}) * N(-d_1^*) P=K∗e−rT∗N(−d2∗)−(S−i=1∑LwiIie−rti)∗N(−d1∗)
其实也就是把所有成分股的红利加起来折算为期初价格,从S中减去。
d 1 = l n ( ( S − ∑ i = 1 L w i I i e − r t i ) / K ) + [ r + ( σ 2 / 2 ) ] T σ T d_1 =\frac{ln((S - \sum\limits_{i=1}^Lw_i\Iota_ie^{-rt_i})/K) + [r+(\sigma^2/2)]T}{\sigma\sqrt{T}} d1=σTln((S−i=1∑LwiIie−rti)/K)+[r+(σ2/2)]T
d 2 = d 1 − σ T d_2 = d1 - \sigma\sqrt{T} d2=d1−σT
其中,wi表示成分股i占股指的比重, I \Iota Ii和ti分别表示成分股i的分红和分红时间。
希腊字母
影响期权价格的主要因素有:标的资产的价格、标的资产的波动率、市场利率、期权到期时间等。我们常用Delta( Δ \Delta Δ)、Gamma( Γ \Gamma Γ)、Vega( ν \nu ν)、Theta( Θ \Theta Θ)、Rho( ρ \rho ρ)这五个希腊字母来描述这些因子对期权价格的影响。
| 名字 | 符号 | 风险因素 | 量化公式 |
|---|---|---|---|
| Delta | Δ \Delta Δ | 标的价格变化 | 权利金变动值/标的价格变动值 |
| Gamma | Γ \Gamma Γ | 标的价格变化 | Delta变动值/标的价格变动值 |
| Vega | ν \nu ν | 波动率变化 | 权利金变动值/波动率变动值 |
| Theta | Θ \Theta Θ | 到期时间变化 | 权利金变动值/到期时间变动值 |
| Rho | ρ \rho ρ | 利率变化 | 权利金变动值/利率变动值 |
Delta ( Δ \Delta Δ)
·Delta用来衡量标的资产价格变动对期权理论价格的影响程度,可以理解为期权价格对标的资产价格变动的敏感性。
看涨期权的Delta计算: Δ C = ∂ C ∂ S = N ( d 1 ) \Delta_C = \frac{\partial{C}}{\partial{S}} = N(d_1) ΔC=∂S∂C=N(d1) ( ∂ \partial ∂是偏微分,这里就是B-S-M期权价格公式对资产价格求偏微分)
看跌期权的Delta计算: Δ P = ∂ P ∂ S = N ( d 1 ) − 1 \Delta_P = \frac{\partial{P}}{\partial{S}} = N(d_1)-1 ΔP=∂S∂P=N(d1)−1
其中 d 1 = l n ( S / K ) + [ r + ( σ 2 / 2 ) ] T σ T d_1 =\frac{ln(S/K) + [r+(\sigma^2/2)]T}{\sigma\sqrt{T}} d1=σTln(S/K)+[r+(σ2/2)]T
回顾前面学习的B-S-M公式,其实Delta就是公式里面的S的系数。
Delta的特性如下:
特性1【取值范围】 看涨期权的Delta取值范围为0~1, 看跌期权的取值范围为-1~0。可以理解为,若资产价格上涨一个单位,则看涨期权的价格就会上涨一些,而看跌期权的价格就会下降一些。
特性2【随标的资产价格变动情况】 当标的价格大于行权价时,随着资产价格的上升,看涨期权的Delta值逐渐变大(趋于1),看跌期权的Delta值也逐渐变大(趋于0) ;
当标的价格小于行权价时,随着资产价格的下降,看涨期权的Delta值逐渐变小(趋于零),看跌期权的Delta值逐渐变小(趋于-1);
特性3【临近到期日时变动情况】 随着到期日的临近,Delta的变化:
看涨期权:
实值期权(标的价格>行权价):Delta收敛于1;
平值期权(标的价格=行权价):Delta收敛于0.5;
虚值期权(标的价格<行权价):Delta收敛于0;
看跌期权:
实值期权(标的价格<行权价):Delta收敛于-1;
平值期权(标的价格=行权价):Delta收敛于-0.5;
虚值期权(标的价格>行权价):Delta收敛于0;
特性4 投资者可以按照1单位资产和Delta单位期权做反向头寸来规避资产组合的价格波动风险。如果策略能完全规避组合的价格波动,则称为Delta中性策略。静态的Delta对冲不能完全规避风险,投资者需要不断依据市场变化调整对冲头寸。
例子:一个投资者持有5单位Delta=0.8的看涨期权和4单位Delta=-0.5的看跌期权,期权的标的相同。若逾期标的资产价格下跌,该投资者的组合是否面临价格波动风险?该如何对冲此类风险?
解析:该资产组合的Delta=5 * 0.8+4 *(-0.5) = 2,因此资产价格下跌将导致组合价值下跌,解决方案有:1.再购入4单位Delta=-0.5的看跌期权;或者2.卖空2单位的标的资产。两个方案都能实现Delta中性。
Gamma ( Γ \Gamma Γ)
Gamma是衡量Delta值对标的资产价格的敏感度,其数学表达式为:
看涨期权: Γ C = ∂ Δ ∂ S = ∂ 2 C ∂ S 2 \Gamma_C = \frac{\partial{\Delta}}{\partial{S}} = \frac{\partial^2{C}}{\partial{S^2}} ΓC=∂S∂Δ=∂S2∂2C
= N ′ ( d 1 ) S σ T = \frac{N'{(d_1)}}{S\sigma\sqrt{T}} =SσTN′(d1) (这一步没看懂,这个结果怎么算出来的?) (N’(d1)是指标准正态分布累积函数的导数,也即其密度函数)
看跌期权: Γ P = ∂ Δ ∂ S = ∂ 2 P ∂ S 2 \Gamma_P = \frac{\partial{\Delta}}{\partial{S}} = \frac{\partial^2{P}}{\partial{S^2}} ΓP=∂S∂Δ=∂S2∂2P
= N ′ ( d 1 ) S σ T = \frac{N'{(d_1)}}{S\sigma\sqrt{T}} =SσTN′(d1) (所以看跌期权的公式和看涨期权是一毛一样的)
Gamma的特性如下:
特性1【取值范围】 Gamma值均为正值;
特性2【随标的资产价格变动情况】 深度实值和深度虚值的Gamma较小, 只有当标的资产价格和执行价相近时Gamma较大,也就是说平值期权的Gamma最大。
特性3【临近到期日时变动情况】 临近到期日时,平价期权的Gamma值趋近于无穷大。实值和虚值期权的Gamma值先变大后变小,随着接近到期日收敛于0 。
特性4 波动率和Gamma的最大值成反比。想一下Gamma曲线,中间高,两头低。波动率越小,Gamma曲线中间部位凸出越高;波动率越大,Gamma曲线中间部位凸出越低。
Vega (v)
Vega用来度量期权价格对波动率的敏感性,该值越大,说明期权价格对波动率越敏感。
看涨期权: ν c = ∂ C ∂ σ = S T N ′ ( d 1 ) \nu_c = \frac{\partial{C}}{\partial{\sigma}} = S\sqrt{T}N'(d_1) νc=∂σ∂C=STN′(d1) (这里也即是B-S-M期权价格公式对波动率求偏微分)
看涨期权: ν c = ∂ P ∂ σ = S T N ′ ( d 1 ) \nu_c = \frac{\partial{P}}{\partial{\sigma}} = S\sqrt{T}N'(d_1) νc=∂σ∂P=STN′(d1) (所以看跌期权的公式和看涨期权是一毛一样的)
Vega的特性如下:
特性1【取值范围】 Vega值总为正值,也即是说期权价格与波动率成正比;
特性2【随标的资产价格变动情况】 深度实值和深度虚值的Vega较小, 只有当标的资产价格和执行价相近时Vegga较大,也就是说平值期权的Vegga最大。
特性3【临近到期日时变动情况】 越临近到期日,Vega越小 ,也即标的资产波动率对期权价格影响变小。
Theta ( Θ \Theta Θ)
Theta用来衡量期权价格对到期日的敏感度。
看涨期权: ν c = ∂ C ∂ t = S σ 2 T N ′ ( d 1 ) − K e − r T r N ( d 2 ) \nu_c = \frac{\partial{C}}{\partial{t}} = \frac{S\sigma}{2\sqrt{T}}N'(d_1) - Ke^{-rT}rN(d_2) νc=∂t∂C=2TSσN′(d1)−Ke−rTrN(d2) (这里也即是B-S-M期权价格公式对距离到期日的时间t求偏微分)
看涨期权: ν c = ∂ P ∂ t = S σ 2 T N ′ ( d 1 ) − K e − r T r ( N ( d 2 ) − 1 ) \nu_c = \frac{\partial{P}}{\partial{t}} = \frac{S\sigma}{2\sqrt{T}}N'(d_1) - Ke^{-rT}r(N(d_2)- 1) νc=∂t∂P=2TSσN′(d1)−Ke−rTr(N(d2)−1)
Theta的特性如下:
特性1【取值范围】 Theta值总为负值,也即是说期权价格随着到期日的临近而降低;
特性2【随标的资产价格变动情况】 深度实值和深度虚值的Theta绝对值较小, 只有当标的资产价格和执行价相近时Theta绝对值较大,也就是说平值期权的Theta绝对值最大。
Rho ( ρ \rho ρ)
Rho用来度量期权价格对利率变动的敏感程度。
看涨期权: ρ c = ∂ C ∂ r = K e − r T N ( d 2 ) \rho_c = \frac{\partial{C}}{\partial{r}} = Ke^{-rT}N(d_2) ρc=∂r∂C=Ke−rTN(d2)
看跌期权: ρ p = ∂ P ∂ r = K e − r T ( N ( d 2 ) − 1 ) \rho_p = \frac{\partial{P}}{\partial{r}} = Ke^{-rT}(N(d_2)-1) ρp=∂r∂P=Ke−rT(N(d2)−1)
Rho的特性如下:
特性1【取值范围】 看涨期权Rho是正值,看跌期权Rho是负值;
特性2【随标的资产价格变动情况】 Rho随标的资产价格单调递增。对于看涨期权,Rho是正值,单调递增就意味着标的资产价格越高,Rho值越大,也即利率对期权价格影响越大; 对于看跌期权,Rho是负值,单调递增意味着标的资产价格越低,Rho的绝对值越大,也即利率对期权价格影响越大。
特性3【临近到期日时变动情况】 随着期权到期,Rho值单调收敛至0。
波动率
期权交易的核心是关注波动率的波动,期权交易也被称为波动率交易。标准资产波动率与期权价格正相关。
历史波动率 σ H \sigma_H σH:使用持有期权之前的标的价格数据计算出来的,是过去真实存在的波动率。历史波动率是当前期权定价的重要参考。
实现波动率 σ R \sigma_R σR:使用持有期权期间的标的价格数据计算出来的,是持有期间真实存在的波动率。实现波动率是计算持有期权期间损益的主要指标。
隐含波动率 σ I \sigma_I σI:是通过已知的期权价格倒推出来的波动率,是隐含在期权价格里面的。隐含波动率是观察市场情绪的重要因素。如果计算出的隐含波动率上升,则意味着市场大多数参与者认为市场会出现大的波动。绝大多数情况下,下跌的速度是快于上涨的速度的,因此隐含波动率就成为预测市场下跌的恐慌性指标。VIX指数就是根据这一原理设计出来的。VIX(Volatility Index)也即波动率指数,是芝加哥期权交易所上市的品种。