图（最短路径算法————迪杰斯特拉算法和弗洛伊德算法）
一：
最短路径算法
1. 迪杰斯特拉算法
2. 弗洛伊德算法
二：
1.
迪杰斯特拉算法
求
从源点到其余各点的最短路径
依
最短路径的长度递增
的次序求得各条
路径
路径长度最短
的最短路径的特点：
在这条路径上，
必定只含一条弧
，并且这条
弧的
权值最小
。
下一条
路径长度次短
的最短路径的特点：
它只可能有两种情况：或是
直接从源点到该
点
(
只含一条弧
)
；
或者是
从源点经过顶点
v
1
，再到达该顶点
(
由两条弧组成
)
。
再下一条
路径长度次短
的最短路径的特点
:
它可能有三种情况：或者是
直接从源点到该
点
(
只含一条弧
)
；
或者是
从源点经过顶点
v
1
，再到达该顶点
(
由两条弧组成
)
；或者是
从源点经过顶点
v
2
，再到达该顶点。
其余最短路径的特点：
它或者是
直接从源点到该点
(
只含一条弧
)
；
或者是
从源点经过已求得最短路径的顶点，
再到达该顶点
。
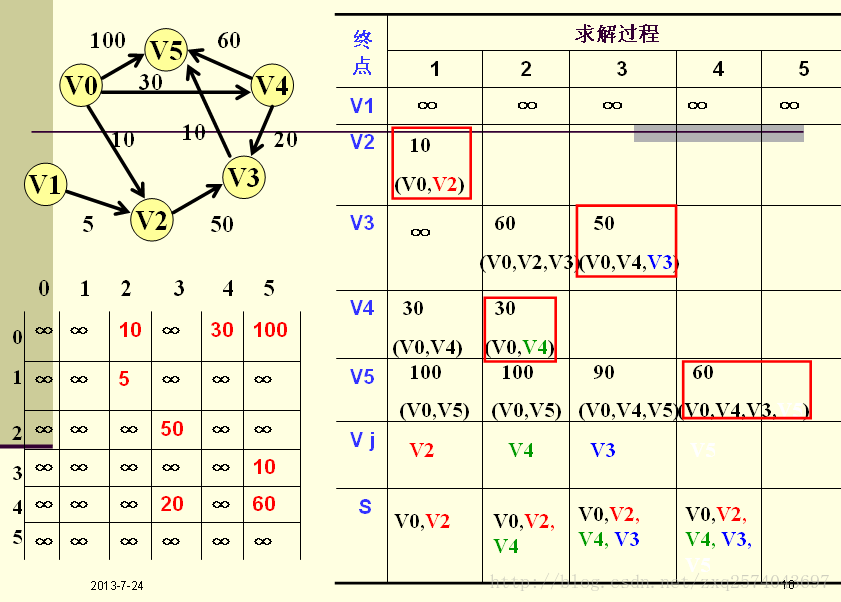
迪杰斯特拉算法
算法：
(a)
初始化：
用起点v到该顶点w的直接边(弧)初始化最短路径，否则设为∞；
(b)
从未求得最短路径的终点中选择路径长度最小的终点u：即求得v到u的最短路径；
(c)
修改最短路径：
计算u的邻接点的最短路径，若(v,…,u)+(u,w)<(v,…,w)，则以(v,…,u,w)代替。
(d)
重复
(b)-(c)
，直到求得v到其余所有顶点的最短路径。
特点：总是按照从小到大的顺序求得最短路径。
顶点
A
到其他顶点的最短路径
Dijkstra
算法可描述如下：
¶
初始化：
S
←
{
v
0
};
dist
[
j
]
←
Edge
[0][
j
],
j
= 1, 2, …,
n
-
1;
//
n
为图中顶点个数
·
求出最短路径的长度：
dist
[
k
]
←
min{
dist
[
i
] },
i
Î
V
-
S
;
S
←
S
U
{
k
};
¸
修改：
dist
[
i
]
←
min{
dist
[
i
],
dist
[
k
] +
Edge
[
k
][
i
] },
对于每一个
i
Î
V
-
S
;
¹
判断： 若S = V, 则算法结束，否则转
二：
弗洛伊德算法
求每对顶点之间的最短路径。
依次计算矩阵A(0)，A(1)，…，A(n)。
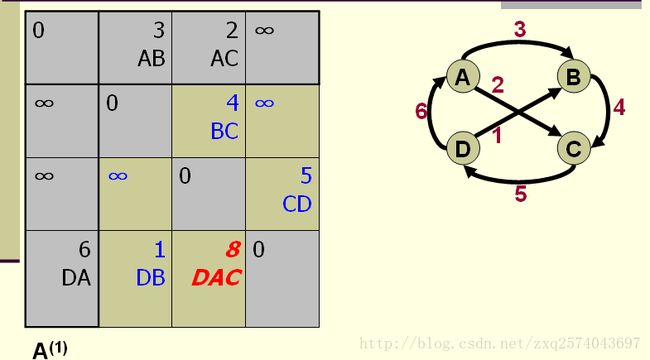
A
(0)
为邻接矩阵，
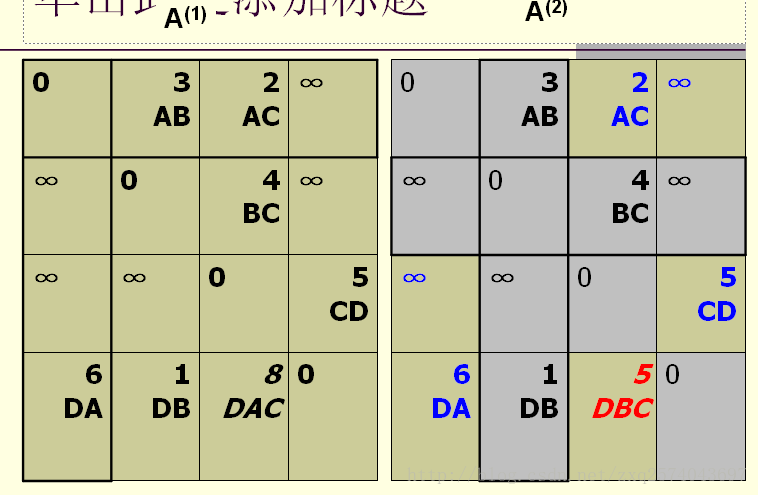
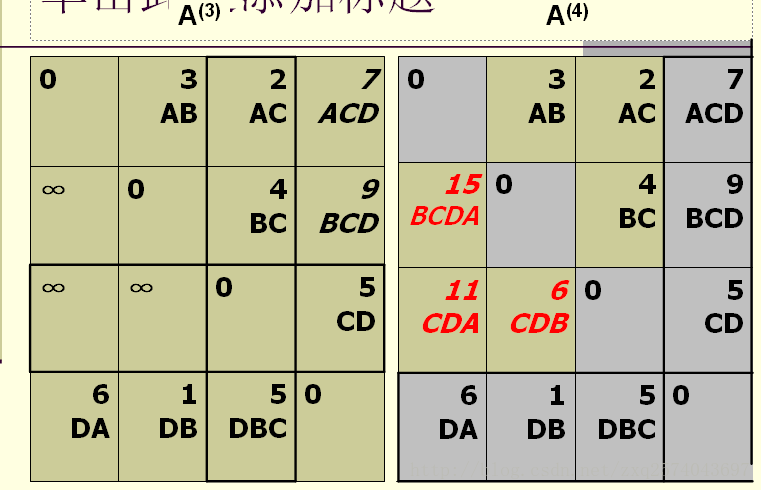
计算A(k)时，
A (k) (i,j)=min{A (k-1) (i,j), A (k-1) (i,k)+A (k-1) (k,j)} 。
A (k) (i,j)=min{A (k-1) (i,j), A (k-1) (i,k)+A (k-1) (k,j)} 。
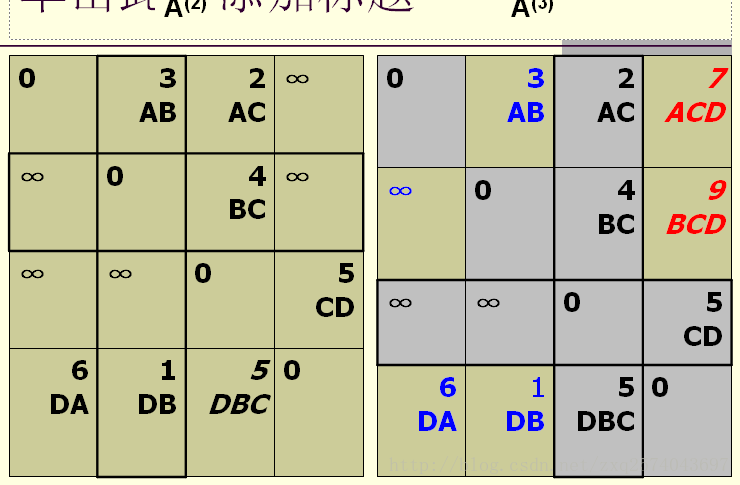
A(0) [i][j]是从顶点vi 到vj , 中间顶点是v0的最短路径的长度, A(k) [i][j]是从顶点vi 到vj , 中间顶点的序号不大于k的最短路径的长度, A(n-1)[i][j]是从顶点vi 到vj 的最短路径长度。
弗洛伊德算法的基本思想是：
从
v
i
到
v
j
的所有可能存在的路径中，选出
一条长度最短的路径
。
n
次试探
:
若
//
路径中不含其它顶点
若
//
路径中所含顶点序号不大于
0
若
{v
i
,…,v
1
}, {v
1
,…,v
j
}
存在，
则存在一条路径
{v
i
, …, v
1
, …v
j
}
//
路径中所含顶点序号不大于
1
…
依次类推，则
vi
至
vj
的最短路径应是上述
这些路径中，路径长度最小者
。
求每对顶点之间的最短路径
弗洛伊德算法
技巧：计算A(k)的技巧。
第
k
行、第
k
列、对角线的元素保持不变，
对其
余元素，考查
A(i,j)
与
A(i,k)+A(k,j)
（第k列i“行”元素加上第k行j“列”元素，简记为“行+列”），如果后者更小则替换A(i,j)，同时修改路径。
本节给出的求解最短路径的算法不仅适用于带权有向图，对带权无向图也可以适用。因为带权无向图可以看作是有往返二重边的有向图，只要在顶点vi 与vj 之间存在无向边(vi , vj )，就可以看成是在这两个顶点之间存在权值相同的两条有向边< vi , vj >和< vj , vi >。
试利用Dijkstra算法求下图中从顶点1到其他各顶点间的最短路径，写出执行算法过程中各步的状态