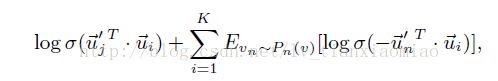LINE:Large-scale Information Network Embedding介绍
传统的network embedding的方法不太适用于大规模的网络运算
因为像MDS, LLE这样的线性映射方法都是需要矩阵操作的
凡是这样的操作,是比较难以实现分布式的处理,导致不能处理大的网络
但是在2015年微软的唐建等人提出了另一种network embedding的方式,能够处理大规模数据
这里就简单的记录一下这个LINE的处理方式,看有什么不一样的
LINE这种方式的出发点跟其他的算法差不多,都是对于一个大的网络G(V, E)
把网络中的所有的节点v, 映射到一个d维的向量中, 然后尽量保持原有网络的结构
在LINE中想要保持的结构就是1度关系和二度关系
先说1度关系:p1'代表的是原始的一度关系
p1'(i, j) = wij/W, 这里的wij是边的权值, W是所有边的权重之和
p1代表的是映射之后的1度关系表示, 那么p1(i, j) = 1/(1 + e^(-ui * uj))
ui代表点i映射后的向量, uj代表点j映射后的向量,ui*uj代表的是点积
O1 = d(p1'(., .), p1(., .))
这里的O1就是优化目标函数, d是距离公式, LINE中用的是KL散度,也就是
O1 = -∑wij*logp1(i, j)
这个优化的目标
然后再说一下2度关系, 定义p2'为原始图中的节点的二度关系
p2'(vj | vi) = wij /di wij表示i和j之间的权重, di表示的是节点i的outdegree , di = ∑wi·
ui就是vi映射后的向量, u’j 是vj映射后的上下文向量,这里作者也没有具体去描述, u‘k代表V中所有点的上下文向量
这里的上下文向量好像也是需要优化得到了
可以看到这个p2表示的二段关系其实也还是比较简单的, 基本上就是根据连接的近邻点来判断, 其实这里我也没看明白p2和p1到底有什么区别
主要是这个u'j向量说的不够清楚,不过这里可以自己脑补
优化的目标函数为:
有了目标函数了,那么接下来就是一个好的想法都要涉及到的地方,那就是优化
文中说道,要优化这个模型,特别是p2还是比较费时的,因为要计算每一个点同其他点的关系,这里提出了一种类似于negative sample的方式
我想这个边采样的方式就是所有连接的边都是正例, 而负例不需要用所有的节点来表示,而是采样一些不相干的节点来做噪声
最后是提出了下面的目标函数
此目标函数的含义很明确, 第一项是正例, 第二项是采样得到的负例, 第一项中的u'j 和ui越相似越好
第二项中的u'n与ui是越不相似越好, 这个可以说是O2的一个替代目标函数
点的问题解决了接下来提出了边的问题,因为O1和O2都是会乘上权重wij,所以呢如果wij比较大的话,那么会出现梯度问题
这样就不能够得到合适的学习率,针对这个问题,文中提出了一种edge sample的方法
据文中表达的观点,对于带权值的边最好转化成为不带权值的边,也就是连接就为1, 不连接就为0
权值转换可以表示为如果权值为5的话,那么相当于连接了五条边这样的方式
这样如果用全部边转换的话,那么数据量肯定会变的很大,所以才需要边采样来尽量保持一下分布
至于edge sample的具体过程,文中也没有具体的描述
最后讨论了两个问题,一个是对于那么邻居非常少的点是如何处理,另一个问题是对于新的点如何处理
到这里文章就进入了实验部分,可以说一篇论文也无法把所有的问题都讲清楚, 还有很多不清楚的估计都要自己脑补了