FPGA实现全流水arccos，arcsin，任意次开放操作

项目背景

因为算法需要降低难度，所以对算法进行了调整，调整过后需要使用arccos，arcsin，三次开平方根操作，所以查找资料编写了一下IP，用于使用，希望能帮到大家，如果对你有帮助请点赞，关注加收藏啊。

任意次开方根操作,单浮点精度，流水线操作

原理：就是对输入数据进行指数和对数变换，将开方根操作改成指数，对数和乘法运算，有因为ln是有输入范围的，所以需要先对输入数据进行sign判断。公式如下

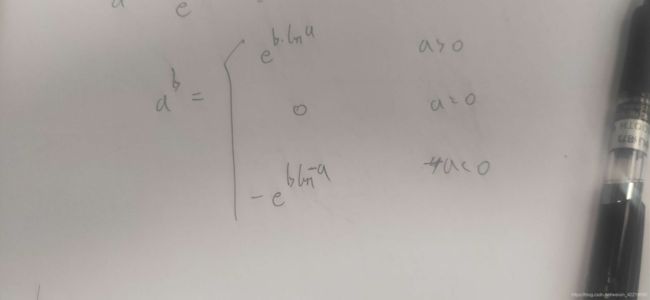
module cubicroot #(
    yinzi = 32'h3EAAAAAB    //开根号因子，对于三次开方根 = 1/3 ； 
)
(
/*
模块功能： root                 
任意幂次开方根备注： 
1.纯浮点计算
2.流水线计算    
*/
    // System
    input clk,
    input rst_n,
    // Input
    input din_en,
    input [31:0] din,
    input din_last,     // 略
    // Output 
    output dout_en,
    output [31:0] dout,
    output dout_last    //略
    );

//--------------- Step0 判断正负值----------------
reg din_en_r0 = 0;
reg [31:0] din_r0 = 0;
always @ (posedge clk)
    begin
        din_en_r0 <= din_en;
        din_r0 <= din;
    end

reg [1:0] result=0;// 0:表示输入为0； 1：表示输入为正数； 2：表示输入为负数
always @ (posedge clk) 
    begin
        if(din_en)
            begin
                if(din == 0)
                    begin
                        result <= 0;
                    end
                else if(din[31] == 0)
                    begin
                        result <= 1;
                    end
                else
                    begin
                        result <= 2;
                    end
            end
    end

//----------------Step1  取log|x|-------------------
wire dout_log_en;
wire [31:0] dout_log;
reg [1:0] result_r1 [22:0];
integer i;
always @ (posedge clk)
    begin
        for (i=0;i<22;i=i+1)
            begin
                result_r1[i+1] <=result_r1[i];
            end
        result_r1[0] <= result;
    end

//23延迟
floating_log log (
  .aclk(clk),                                  // input wire aclk
  .s_axis_a_tvalid(din_en_r0),            // input wire s_axis_a_tvalid
  .s_axis_a_tready(),            // output wire s_axis_a_tready
  .s_axis_a_tdata({1'b0,din_r0[30:0]}),              // input wire [31 : 0] s_axis_a_tdata
  .m_axis_result_tvalid(dout_log_en),  // output wire m_axis_result_tvalid
  .m_axis_result_tready(1'b1),  // input wire m_axis_result_tready
  .m_axis_result_tdata(dout_log)    // output wire [31 : 0] m_axis_result_tdata
);
wire [1:0] result_log = result_r1[22];

//---------------Step 取1/3*log|x|----------------
wire dout_mul_en;
wire [31:0] dout_mul;
reg [1:0] result_r3 [6:0];
integer k;
always @ (posedge clk)
    begin
        for (k=0;k<6;k=k+1)
            begin
                result_r3[k+1] <=result_r3[k];
            end
        result_r3[0] <=  result_log;
    end

floating_mul your_instance_name (
  .aclk(clk),                                  // input wire aclk
  .s_axis_a_tvalid(dout_log_en),            // input wire s_axis_a_tvalid
  .s_axis_a_tready(),            // output wire s_axis_a_tready
  .s_axis_a_tdata(dout_log),              // input wire [31 : 0] s_axis_a_tdata
  .s_axis_b_tvalid(dout_log_en),            // input wire s_axis_b_tvalid
  .s_axis_b_tready(),            // output wire s_axis_b_tready
  .s_axis_b_tdata(yinzi),              // input wire [31 : 0] s_axis_b_tdata             // 1/3
  .m_axis_result_tvalid(dout_mul_en),  // output wire m_axis_result_tvalid
  .m_axis_result_tready(1'b1),  // input wire m_axis_result_tready
  .m_axis_result_tdata(dout_mul)    // output wire [31 : 0] m_axis_result_tdata
);
wire [1:0] result_mul = result_r3[6];

//----------------Step3 取e.^(1/3*log|x|)---------------
wire dout_en_e;
wire [31:0] dout_e;
reg [1:0] result_r2 [20:0];
integer j;
always @ (posedge clk)
    begin
        for (j=0;j<20;j=j+1)
            begin
                result_r2[j+1] <=result_r2[j];
            end
        result_r2[0] <= result_mul;
    end

//21 延迟
floating_exponential exponeetial(
  .aclk(clk),                                  // input wire aclk
  .s_axis_a_tvalid(dout_mul_en),            // input wire s_axis_a_tvalid
  .s_axis_a_tready(),            // output wire s_axis_a_tready
  .s_axis_a_tdata(dout_mul),              // input wire [31 : 0] s_axis_a_tdata
  .m_axis_result_tvalid(dout_en_e),  // output wire m_axis_result_tvalid
  .m_axis_result_tready(1'b1),  // input wire m_axis_result_tready
  .m_axis_result_tdata(dout_e)    // output wire [31 : 0] m_axis_result_tdata
);

wire [1:0] result_e = result_r2[20];

//---------Step  选择输出------------------
assign dout_en = dout_en_e;
assign dout = result_e==0?0:(result_e==1?dout_e:({1'b1,dout_e[30:0]}));

endmodule

单浮点精度，流水线操作，已经验证过结果了，没有问题，采用vivado写的，
yinzi = 32’h3EAAAAAB //开根号因子，对于三次开方根 = 1/3 ；
如果需要开N次根，只需要给yinzi = 1/N(浮点表示就可以) ，关于如何表示可以使用浮点数转换小工具

acos 和 asin 的计算,定点操作，流水线操作

原理：采用毕达哥拉斯和三角比，需要用到的IP有cordic (其中的sqrt和arctan)

module arccos_atan(
/*
模块功能： acos   也可以用于求asin   
原理：毕达哥拉斯定理和三角比             
1.纯定点计算
2.流水线计算    
*/

// System
input clk,
input rst_n,
// Input
input din_en,
input signed [15:0] din,    //fix16_15 
input din_last,     // 略
// Output 
output dout_en,
output [17:0] dout,     //fix18_15
output dout_last    //略
    );

//------------------ Step0 x^2--------------- 定点
reg signed [30:0] X2 = 0;
reg dout_en_X2 = 0;     //fix31_30
reg [15:0] din_r1;
always @ (posedge clk)
    begin
        dout_en_X2 <= din_en;
        din_r1 <= din;
    end
always @ (posedge clk)
    begin
        if(din_en)
            begin
                X2 <= din * din; 
            end
        else
            begin
                X2 <= 0;
            end
    end

//---------------- Step1 1-x^2-----------  定点
reg signed [30:0] X2_1 = 0;     //fix31_30
reg [15:0] din_r2;
reg signed [30:0] One = {1'b0,30'h3fffffff};
reg dout_en_X2_1 = 0;
always @ (posedge clk)
    begin
        dout_en_X2_1 <= dout_en_X2;
        din_r2 <=  din_r1;
    end
always @ (posedge clk)
    begin
        X2_1 <= One - X2;
    end



//--------------- Step 2 root2(1-x^2)---------- 定点
wire dout_en_root2;
wire [15:0]dout_root_2;
reg [15:0] din_x [15:0];
integer i;
always @ (posedge clk)
    begin
        for (i=0;i<15;i=i+1)
            begin
                din_x[i+1] <=din_x[i];
            end
        din_x[0] <= din_r2;
    end

wire [15:0] dout_xx = din_x[15];
//16 延迟
cordic_root2    root2(      
  .aclk(clk),                                        // input wire aclk
  .s_axis_cartesian_tvalid(dout_en_X2_1 ),  // input wire s_axis_cartesian_tvalid
  .s_axis_cartesian_tdata({1'b0,X2_1}),    // input wire [31 : 0] s_axis_cartesian_tdata
  .m_axis_dout_tvalid(dout_en_root2),            // output wire m_axis_dout_tvalid
  .m_axis_dout_tdata(dout_root_2)              // output wire [31 : 0] m_axis_dout_tdata
);

//----------------- 四象限正切 ， 因为y一定是大于0，则输入定会在第一象限与第二象限，其输出也一定会是0-pi之间
wire dout_en_atan4;
wire [17:0] dout_atan4; //FIX 18_15
// 22 延迟
cordic_atan4 S4 (       
  .aclk(clk),                                        // input wire aclk
  .s_axis_cartesian_tvalid(dout_en_root2),  // input wire s_axis_cartesian_tvalid
  .s_axis_cartesian_tdata({7'd0,dout_root_2[15],dout_root_2,7'd0,dout_xx[15],dout_xx}),    // input wire [47 : 0] s_axis_cartesian_tdata
  .m_axis_dout_tvalid(dout_en_atan4),            // output wire m_axis_dout_tvalid
  .m_axis_dout_tdata(dout_atan4)              // output wire [23 : 0] m_axis_dout_tdata
);

assign dout_en = dout_en_atan4;
assign dout = dout_atan4;
endmodule

定点，流水线操作，已经验证过结果了，没有问题，采用vivado写的，不同位宽延迟略有不同，你需要根据实际生成IP延迟进行修改，以上是求arccos，求arcsin需要添加判断，因为四象限正切的值一定会是正值，而arcsin是-pi/2 到 pi/2之间，所以最后需要修改下，很简单。

一定要关注点赞加收藏啊