内存分配------------伙伴系统
首先(Buddy)伙伴的定义:
- 两个块大小相同
- 两个块地址连续
- 两个块必须是同一个大块中分离出来的
适用条件:
伙伴系统一般使用于大内存块的分配,并且是2的幂次
算法方式:
申请:从维护的数据结构中寻找合适所要求大小的块,如果满足,并且此块的剩余部分大于一半,那么就将剩下一半分割出来,供以后调用
释放:将此块释放,并且搜索此伙伴块是否也是空闲的,如果是,就合并,然后将合并后的块继续判断其伙伴是否是空闲的,依次向上递归合并
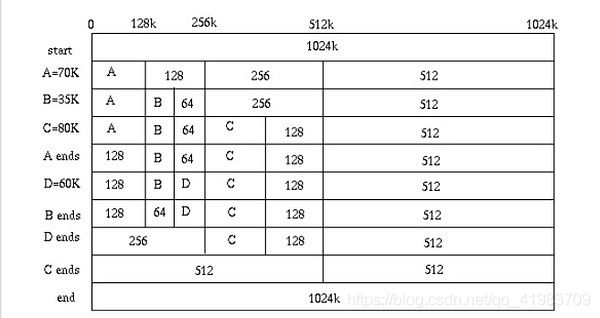
下面用图来简单查看申请和释放的过程:
上图中,首先我们假设我们一个内存块有1024K,当我们需要给A分配70K内存的时候,
1. 我们发现1024K的一半大于70K,然后我们就把1024K的内存分成两半,一半512K。
2. 然后我们发现512K的一半仍然大于70K,于是我们再把512K的内存再分成两半,一半是128K。
3. 此时,我们发现128K的一半小于70K,于是我们就分配为A分配128K的内存。
后面的,B,C,D都这样,而释放内存时,则会把相邻的块一步一步地合并起来(合并也必需按分裂的逆操作进行合并)。
我们可以看见,这样的算法,用二叉树这个数据结构来实现再合适不过了
比如总内存大小为:8
8 0
/ \
4 1 2
/ \ / \
2 3 4 5 6因此,我可以采用完全二叉树,来记录所分配的内存的大小,从而这个内存分配器是非入侵式的,即不在要分配的内存块中写 cookie,申请和释放的时间复杂度都是 O(log N)
实现思路:
伙伴算法的分配器的实现思路是,通过一个数组形式的完全二叉树来监控管理内存,二叉树的节点用于标记相应内存块的使用状态。
申请过程:
比如以上面的二叉树为例,索引为1的节点的内存大小是4,此时分配出去了,那么此时更新父节点的内存大小,即是左右孩子的最大值,即此时0处表示能用内存是4(即右孩子还剩的内存),高层节点对应大的块,低层节点对应小的块,在分配和释放中我们就通过这些节点的标记属性来进行块的分离合并。
释放过程:
比如释放索引为1的节点的内存,加入索引为2的节点处是未分配的,那么通过回溯父节点,来查看右孩子是否是已分配的,来进行合并,然后将索引为0的节点处的大小改为8.
时间复杂度:
由于这是一个完全二叉树,从而申请和释放的时间复杂度都在O(log N)内。
伙伴算法的优点:
对于申请的大内存来说,将是快速的,并且不会产生外部碎片,因为它采用的是最佳适配,因为输入的时候,会调整成2的次幂,从而一定会找到最满足此情况的节点。
缺点:
由于对申请的内存进行2的次幂的上调,那么对于分配65单位的内存来说,就需要分配128大小的内存块,从而造成很大的内部碎片。
下面贴出算法实现:
原始版本是云风的版本,wuwenbin做了改进,https://github.com/cloudwu/buddy
此算法实现是实现的wuwenbin的版本https://github.com/wuwenbin/buddy2
#ifndef __BUDDY_H__
#define __BUDDY_H__
#include
#include
using namespace std;
/*
可分配的最大内存,和保存完全二叉树的数组
class buddy
{
unsigned size;
vector longest;
};
*/
class buddy;
/*
size是整块的内存大小,然后通过数组的形式来构造完全二叉树,
并且每个节点记录了可分配的内存大小
*/
class buddy* buddy_new( int size );
/* 释放这个buddy管理内存 */
void buddy_destroy( class buddy* self );
/* 分配内存 ,返回的是这块内存相对于首位值得偏移量 */
int buddy_alloc(class buddy* self, int size);
/* 释放内存中得块 */
void buddy_free(class buddy* self, int offset);
/* 根据此偏移量,来计算此申请的大小 并返回 */
int buddy_size(class buddy* self, int offset);
/*
将分配的状态打印出来
通过'_ '来表示未分配的块,用 ' * '来表示已分配的块 */
void buddy_dump(class buddy* self);
/* 测试 */
void buddy_text(class buddy* self);
#endif//__BUDDY_H__
组织完全二叉树结构:
class buddy* buddy_new(int size)
{
buddy* self;
unsigned node_size;
int i;
if (size < 1 || !IS_POWER_OF_2(size))
return NULL;
self = new buddy(size);
node_size = size * 2;
//比如申请内存是4
// 8 0
// / \
// 4 1 2
// / \ / \
// 2 3 4 5 6
//这里的完全二叉树是用数组来实现的
//这里的size是2*size-1
for (i = 0; i < 2 * size - 1; ++i)
{
if (IS_POWER_OF_2(i + 1))
node_size /= 2;
self->longest[i] = node_size; //每个完全二叉树中的节点存储的是内存的大小
}
return self;
}分配内存,返回偏移量
int buddy_alloc(class buddy* self, int size)
{
unsigned index = 0;
unsigned node_size;
unsigned offset = 0;
if (self == NULL)
return -1;
if (size <= 0)
size = 1;
else if (!IS_POWER_OF_2(size))
size = Fixsize(size);
//如果此时大内存块中剩余的内存大小不满足申请的大小,就返回
if (self->longest[index] < size)
return -1;
//从根节点开始往下找,
//比如申请内存是4
// 8 0
// / \
// 4 1 2
// / \ / \
// 2 3 4 5 6
//从0的左右子节点开始往下找
//直到找到满足此次内存需求的节点,比如满足2的,应该是从3这个节点返回的
for (node_size = self->size; node_size != size; node_size /= 2)
{
if (self->longest[LEFT_LEAF(index)] >= size)
index = LEFT_LEAF(index);
else
index = RIGHT_LEAF(index);
}
//此内存被占用,从而置为0
self->longest[index] = 0;
offset = (index + 1) * node_size - self->size; //这个计算偏移量,很神奇
//修改其父节点的最大内存,时间复杂度不超过logn
while (index)
{
index = PARENT(index);
self->longest[index] =
MAX(self->longest[LEFT_LEAF(index)], self->longest[RIGHT_LEAF(index)]);
}
//这个offset是指相对于分配的这整块内存的位移,比如是从这整块的位移量4开始,那么offest就是4
return offset;
}释放内存:
void buddy_free(class buddy* self, int offset)
{
unsigned node_size, index = 0;
unsigned left_longest, right_longest;
//首先偏移量是肯定小于这整块内存的
assert(self && offset >= 0 && offset < self->size);
node_size = 1;
//根据偏移,计算处索引
index = offset + self->size - 1;
//通过上溯,将内存进行恢复
for (; self->longest[index]; index = PARENT(index))
{
node_size *= 2;
if (index == 0)
return;
}
self->longest[index] = node_size;
// 合并左右子节点,这个左右是伙伴,并且都是2的幂次,因为是通过完全二叉树实现的
while (index)
{
index = PARENT(index);
node_size *= 2;
left_longest = self->longest[LEFT_LEAF(index)];
right_longest = self->longest[RIGHT_LEAF(index)];
if (left_longest + right_longest == node_size)
self->longest[index] = node_size;
else
self->longest[index] = MAX(left_longest, right_longest);
}
}源代码: