Round18—排序树

知识点：

知道什么是排序树。

单选题：

2-1若二叉搜索树是有N个结点的完全二叉树，则不正确的说法是：(1分)

• 所有结点的平均查找效率是O(logN)
• 最小值一定在叶结点上
• 最大值一定在叶结点上
• 中位值结点在根结点或根的左子树上

解析：首先是审题，这个题说比仅仅是搜索树而且是一个完全二叉树。

那么我们知道这时的时间复杂度就是O（logN）的。

因为排序树的特点就是左边小右边大，因此最小值一定在叶节点上。

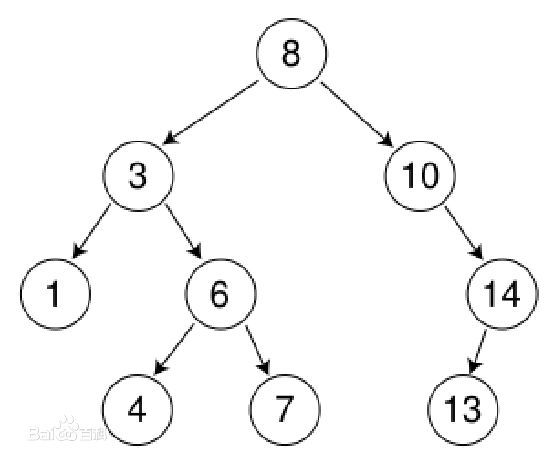
但是最大值就不一定了，如下图：

显然14是最大值所在的节点，但是显然不是叶节点。

完全二叉树的节点数目一点是左边的节点数目不少于右边的结点的数目，不然就不符合完全二叉树的定义了。

因此中位值必然是出现在根节点或者是出现在左子树上。

2-2若一棵二叉树的后序遍历序列是{ 1, 3, 2, 6, 5, 7, 4 }，中序遍历序列是{ 1, 2, 3, 4, 5, 6, 7 }，则下列哪句是错的？(3分)

• 这是一棵完全二叉树
• 2是1和3的父结点
• 这是一棵二叉搜索树
• 7是5的父结点

解析：根据后续遍历我们知道根节点，然后根据根节点在中序遍历当中的位置我们知道左子树与右子树的情况，递归下去我们就能得到整个二叉树。

2-3将{ 32, 2, 15, 65, 28, 10 }依次插入初始为空的二叉搜索树。则该树的前序遍历结果是：(3分)

• 2, 10, 15, 28, 32, 65
• 32, 2, 10, 15, 28, 65
• 10, 28, 15, 2, 65, 32
• 32, 2, 15, 10, 28, 65

解析：根据排序树的插入操作，左边小右边大我们知道第四个才是对的。

2-4下列二叉树中，可能成为折半查找判定树（不含外部结点）的是： (4分)

• 
• 
• 
• 

解析：之前我们分析过这个题目。

2-5若一棵二叉树的前序遍历序列是{ 4, 2, 1, 3, 6, 5, 7 }，中序遍历序列是{ 1, 2, 3, 4, 5, 6, 7 }，则下列哪句是错的？(3分)

• 这是一棵完全二叉树
• 所有的奇数都在叶子结点上
• 这是一棵二叉搜索树
• 2是5的父结点

解析：同样是建树。

2-6将{ 5, 11, 13, 1, 3, 6 }依次插入初始为空的二叉搜索树。则该树的后序遍历结果是：(3分)

• 3, 1, 5, 6, 13, 11
• 3, 1, 6, 13, 11, 5
• 1, 3, 11, 6, 13, 5
• 1, 3, 5, 6, 13, 11

解析：排序树的建树操作以及二叉树的后续遍历。

2-7对二叉搜索树进行什么遍历可以得到从小到大的排序序列？ (1分)

• 前序遍历
• 后序遍历
• 中序遍历
• 层次遍历

解析：因为排序树是左边小右边大，因此我们知道中序遍历输出就是我们的从大到小的排序。

2-8若二叉搜索树是有N个结点的完全二叉树，则不正确的说法是：(1分)

• 平均查找效率是O(logN)
• 最大值一定在最后一层
• 最小值一定在叶结点上
• 中位值结点在根结点或根的左子树上

解析：根据前面的分析我们知道第二个是错的。

2-9已知8个数据元素为（34，76，45，18，26，54，92，65），按照依次插入结点的方法生成一棵二叉搜索树后，最后两层上的结点总数为： (2分)

• 1
• 2
• 3
• 4

解析：考察排序树的建树操作。

2-10下列叙述正确的是（）。 (2分)

• 在任意一棵非空二叉搜索树，删除某结点后又将其插入，则所得二叉搜索树与删除前原二叉搜索树相同。
• 二叉树中除叶结点外, 任一结点X，其左子树根结点的值小于该结点（X）的值；其右子树根结点的值≥该结点（X）的值，则此二叉树一定是二叉搜索树。
• 虽然给出关键字序列的顺序不一样，但依次生成的二叉搜索树却是一样的。
• 在二叉搜索树中插入一个新结点，总是插入到最下层，作为新的叶子结点。

解析：

一颗n个节点的排序树必然是n个节点的值不同.

插入一定是找到无法找因此一定是叶子结点。

编程题：

 

7-1 是否同一棵二叉搜索树 (25 分)

给定一个插入序列就可以唯一确定一棵二叉搜索树。然而，一棵给定的二叉搜索树却可以由多种不同的插入序列得到。例如分别按照序列{2, 1, 3}和{2, 3, 1}插入初始为空的二叉搜索树，都得到一样的结果。于是对于输入的各种插入序列，你需要判断它们是否能生成一样的二叉搜索树。

输入格式:

输入包含若干组测试数据。每组数据的第1行给出两个正整数N (≤10)和L，分别是每个序列插入元素的个数和需要检查的序列个数。第2行给出N个以空格分隔的正整数，作为初始插入序列。最后L行，每行给出N个插入的元素，属于L个需要检查的序列。

简单起见，我们保证每个插入序列都是1到N的一个排列。当读到N为0时，标志输入结束，这组数据不要处理。

输出格式:

对每一组需要检查的序列，如果其生成的二叉搜索树跟对应的初始序列生成的一样，输出“Yes”，否则输出“No”。

输入样例:

4 2
3 1 4 2
3 4 1 2
3 2 4 1
2 1
2 1
1 2
0

输出样例:

Yes
No
No

AC代码： 

#include 
using namespace std;

struct node
{
    int data;
    node *lchild, *rchild;
    node(int data = 0, node *lchild = nullptr, node *rchild = nullptr) : data(data), rchild(rchild), lchild(lchild) {}
};
typedef node *Root;
typedef node *Node;
int N, L;
int a;

Node &Find(int data, Node &treenode)
{
    if(treenode == nullptr)
        return treenode;

    if(data < treenode->data)
        return Find(data, treenode->lchild);

    if(data > treenode->data)
        return Find(data, treenode->rchild);
}

void dfs(Node treenode)
{
    if(treenode == nullptr)
        return ;
    dfs(treenode->lchild);
    printf("%d\n", treenode->data);
    dfs(treenode->rchild);
}

Root buildtree()
{
    scanf("%d", &a);
    Root root = new node(a);
    for(int i = 1; i < N; i++)
    {
        scanf("%d", &a);
        Node &treenode = Find(a, root);
        treenode = new node(a);
    }
    return root;
}

void deleteTree(Node treenode)
{
    if(treenode == nullptr)
        return ;
    deleteTree(treenode->lchild);
    deleteTree(treenode->rchild);
    delete treenode;
}

bool isiDenticalTree(Node treenode1, Node treenode2)
{
    if(treenode1 == nullptr && treenode2 == nullptr)
        return true;
    if(treenode1 == nullptr && treenode2 != nullptr)
        return false;
    if(treenode1 != nullptr && treenode2 == nullptr)
        return false;

    if(treenode1->data != treenode2->data)
        return false;

    if(isiDenticalTree(treenode1->lchild, treenode2->lchild) && isiDenticalTree(treenode1->rchild, treenode2->rchild))
        return true;

    return false;
}

int main()
{
    while(scanf("%d", &N) && N)
    {
        scanf("%d", &L);

        Root root = buildtree();
        //dfs(root);
        for(int i = 0; i < L; i++)
        {
            Root root1 = buildtree();
            if(isiDenticalTree(root, root1))
                printf("Yes\n");
            else
                printf("No\n");
            deleteTree(root1);
        }
    }
    return 0;
}

7-2 是否完全二叉搜索树 (30 分)

将一系列给定数字顺序插入一个初始为空的二叉搜索树（定义为左子树键值大，右子树键值小），你需要判断最后的树是否一棵完全二叉树，并且给出其层序遍历的结果。

输入格式：

输入第一行给出一个不超过20的正整数N；第二行给出N个互不相同的正整数，其间以空格分隔。

输出格式：

将输入的N个正整数顺序插入一个初始为空的二叉搜索树。在第一行中输出结果树的层序遍历结果，数字间以1个空格分隔，行的首尾不得有多余空格。第二行输出YES，如果该树是完全二叉树；否则输出NO。

输入样例1：

9
38 45 42 24 58 30 67 12 51

输出样例1：

38 45 24 58 42 30 12 67 51
YES

输入样例2：

8
38 24 12 45 58 67 42 51

输出样例2：

38 45 24 58 42 12 67 51
NO

AC代码：

#include 
using namespace std;

const int maxn = 10000 + 5;
struct node
{
    int data;
    node *lchild, *rchild;
    node(int data = 0, node *lchild = nullptr, node *rchild = nullptr) : data(data), rchild(rchild), lchild(lchild) {}
};
typedef node *Root;
typedef node *Node;
int N, L;
bool isflag;
int a;

Node &Find(int data, Node &treenode)
{
    if(treenode == nullptr)
        return treenode;

    if(data > treenode->data)
        return Find(data, treenode->lchild);

    if(data < treenode->data)
        return Find(data, treenode->rchild);
}

void dfs(Node treenode)
{
    if(treenode == nullptr)
        return ;
    dfs(treenode->lchild);
    printf("%d\n", treenode->data);
    dfs(treenode->rchild);
}

Root buildtree()
{
    scanf("%d", &a);
    Root root = new node(a);
    for(int i = 1; i < N; i++)
    {
        scanf("%d", &a);
        Node &treenode = Find(a, root);
        treenode = new node(a);
    }
    return root;
}

void deleteTree(Node treenode)
{
    if(treenode == nullptr)
        return ;
    deleteTree(treenode->lchild);
    deleteTree(treenode->rchild);
    delete treenode;
}

void bfs(Node root)
{
    queue que;
    que.push(root);

    bool flag = false;
    while(!que.empty())
    {
        Node treenode = que.front();
        que.pop();
        if(flag)
            printf(" ");
        printf("%d", treenode->data);
        flag = true;

        Node lchild = treenode->lchild;
        Node rchild = treenode->rchild;
        if(lchild != nullptr)
            que.push(lchild);
        if(rchild != nullptr)
            que.push(rchild);
    }
    printf("\n");
}

bool isFull(Root root)
{
    queue que;
    que.push(root);

    bool flag = false;
    while(!que.empty())
    {
        Node treenode = que.front();
        que.pop();
        //printf("%d\n", treenode->data);

        if(flag && (treenode->lchild != nullptr || treenode->rchild != nullptr))
            return false;
        if(treenode->lchild == nullptr && treenode->rchild != nullptr)
            return false;

        Node lchild = treenode->lchild;
        Node rchild = treenode->rchild;
        if(lchild != nullptr)
            que.push(lchild);
        if(rchild != nullptr)
            que.push(rchild);

        if(rchild == nullptr && lchild == nullptr)
            flag = true;
        else if(rchild == nullptr && lchild != nullptr)
            flag = true;
    }

    return true;
}

int main()
{

    scanf("%d", &N);
    Root root = buildtree();

    bfs(root);

    //printf("%d\n", root->data);

    if(isFull(root))
        printf("YES\n");
    else
        printf("NO\n");

    return 0;
}

解析：这个题将判断是否是完全二叉树单独拿出来写得，看一下这个博客吧挺好的。