数据结构---栈和队列（结构体实现）

目录

 

栈（LIFO）

顺序栈(sequential stack)及其基本运算的实现

共享栈(share stack)

链栈及其基本运算的实现

队列（Queue，FIFO）

顺序队(sequential queue)及其基本运算的实现

环形队列（或循环队列，circular queue)及其基本运算的实现

用队列中元素个数代替队尾指针的环形队列及其基本运算的实现

链队(linked queue)及其基本运算的实现

不带头结点只有一个尾结点指针rear的循环单链表实现的链队及其基本运算的实现

---

栈（LIFO）

栈(stack)是一种只能在一端进行插入或删除操作的线性表。

栈顶(top)：允许进行插入、删除操作的一端

栈底(bottom)：另一端称为栈底

进栈或入栈(push)：插入操作

出栈或退栈(pop)：栈的删除操作

n个不同元素通过一个栈产生的出栈序列的个数为。

顺序栈(sequential stack)及其基本运算的实现

栈可以像线性表一样采用顺序存储结构进行存储，即分配一块连续的存储空间来存放栈中的元素，并用一个变量(如top)指向当前的栈顶元素，以反映栈中元素的变化。

顺序栈(SqStack)的声明

#define MaxSize 50
typedef int ElemType;

typedef struct{
    ElemType data[MaxSize];        //连续内存空间存放栈中元素
    int top;            //存放栈顶元素在data数组中的下标    
}SqStack;

采用栈指针 s (不同于栈顶指针top)的方式创建和使用顺序栈。

初始时，为空栈，设置s->top = -1，有：

栈空的条件：s->top == -1;

栈满的条件：s->top == MaxSize - 1;                                                 

元素e的进栈操作：先将栈顶指针top增1，然后将元素e放在栈顶指针处。

出栈操作：先将栈顶指针top处的元素取出放在e中，然后将栈顶指针减1。     \\栈顶指针top实际上是栈顶元素的数组下标

初始化栈 initStack(&s) —— 时间复杂度为

创建一个空栈，由s指向它。即分配一个顺序栈空间，并将栈顶指针设置为-1。

void initStack(SqStack* &s){
    s = (SqStack*)malloc(sizeof(SqStack));    //分配空间，首地址存放在s中
    s->top = -1;
}

 销毁栈 DestroyStack(&s) —— 时间复杂度为

void DestroyStack(SqStack* &s){
    free(s);
}

判断栈是否为空 StackEmpty(&s) —— 时间复杂度为

运用栈空判断条件是否成立

bool StackEmpty(SqStack *s){
    return s->top == -1;
}

进栈 Push(&s, e) —— 时间复杂度为

要先判断栈是否已满

bool Push(SqStack *s, ElemType e){
    if(s->top == MaxSize-1) return false;
    else
        s->top++;
        s->data[s->top] = e;
        return true;
}

出栈 Pop(&s, &e) —— 时间复杂度为

首先判断栈是否为空

bool Pop(SqStack* &s, ElemType &e){
    if(s->top == -1) return false;
    else
        e = s->data[s->top];
        s->top--;
        return false;
}

取栈顶元素 GetTop(s, &e) —— 时间复杂度为

首先判断栈是否为空

bool GetTop(SqStack *s, ElemTypee &e){
    if(s->top == -1) return false;
    e = s->data[s->top];
    return true;
}

应用：设计一个算法利用顺序栈判断一个字符串是否为对称串。所谓对称串指从左向右读和从右向左读的序列相同。

#include 
using namespace std;
#define MaxSize 50
typedef char ElemType;
typedef struct {
	ElemType data[MaxSize];
	int top;
}SqStack;
void initStack(SqStack* &s) {
	s = (SqStack*)malloc(sizeof(SqStack));
	s->top = -1;
}
void Push(SqStack* &s, ElemType e) {
	if (s->top != MaxSize - 1) {
		s->top++;
		s->data[s->top] = e;
	}
}
void Pop(SqStack* &s, ElemType &e) {
	if (s->top != -1) {
		e = s->data[s->top];
		s->top--;
	}
}
void ArrayCreateStack(SqStack* &s, ElemType a[], int n) {
	initStack(s);
	for (int i = 0; i < n; i++)
		Push(s, a[i]);
}
bool SymmetricArray(ElemType a[], int n) {
	SqStack *s;
	ArrayCreateStack(s, a, n);
	for (int i = 0; i < n/2; i++) {
		ElemType j;
		Pop(s, j);
		if (j != a[i]) return false;
	}
	return true;
}
int main() {
	char a1[] = "asdfggfdsa";
	char a2[] = "1234567890";
	cout << SymmetricArray(a1, 10) << endl;
	cout << SymmetricArray(a2, 10) << endl;

	system("pause");
}

共享栈(share stack)

用一个数组来实现两个栈。让一个栈的栈底为数组的始端，即下标为0处；另一个栈的栈底位数组的末端，即下标为MaxSize-1。这样， 在两个栈中进栈时，栈顶向中间伸展。

栈空的条件：栈1空为 top1 == -1；栈2空为 top2 == MaxSize。

栈满的条件：top1 == top2 - 1。

元素e进栈操作：进栈1操作为{ top1++；data[top1] = e; }；进栈2操作为{ top2--；data[top2] = e; }。

出栈e操作：出栈1操作为{ e = data[top1]；top1--; }；出栈2操作为{ e = data[top2]；top2++; }

该共享栈用data、top1、top2来标识。

共享栈的声明

typedef struct{
    ElemType data[MaxSize];
    int top1, top2;
}DStack;

在实现共享栈的基本运算算法时需要增加一个形参i，用来指出是对哪个栈进行操作。

链栈及其基本运算的实现

采用链式存储结构的栈称为链栈(linked stack)。这里采用带头结点的单链表来实现链栈。

链栈的优点是不存在栈满上溢出的情况。规定栈的所有操作都是在单链表的表头进行的（因为带有头结点，在其后插入或删除节点都很方便，时间复杂度为）

如图为头结点指针为s的链栈，首结点是栈顶结点，尾结点是栈底结点。

链栈的声明

typedef struct linknode{
    ElemType data;
    struct linknode* next;
}LinkStNode;

在以s为头结点指针的链栈（简称链栈s）中：

栈空的条件：s->next = NULL;

不存在栈满

元素e的进栈操作：新建一个结点存放元素e（由p指向它），将结点p插入到头结点之后。

出栈操作：取出首结点的data值并将其删除。

初始化栈 initStack(&s) —— 时间复杂度为

该运算创建出一个空链栈s。实际上是创建链栈的头结点，并将其next域置为NULL。

void initStack(LinkStNode* &s){
    s = (LinkStNode*)malloc(sizeof(LinkStNode));
    s->next = NULL;
}

销毁栈 DestroyStack(&s) —— 时间复杂度为

 释放链栈s占用的全部结点空间，和单链表的销毁算法完全相同。

void DestroyStack(LinkStNode* &s){
    LinkStNode *pre = s, *p = s->next;
    while(p!=NULL){
        free(pre);
        pre = p;
        p = pre->next;
    }
    free(pre);
}

 判断栈是否为空 StackEmpty(s)

bool StackEmpty(LinkStNode *s){
    return s->next==NULL;
}

进栈 Push(&s, e)  —— 时间复杂度为

新建一个结点，用于存放元素e（由p指向它），然后将其插入到头结点之后作为新的首结点。

void Push(LinkStNode* &s, ElemType e){
    LinkStNode *p;
    p = (LinkStNode*)malloc(sizeof(LinkStNode));
    p->data = e;
    p->next = s->next;
    s->next = p;
}

出栈 Pop(&s, &e)  —— 时间复杂度为

首先检查栈是否为空。

bool Pop(LinkStNode* &s, ElemType &e){
    LinkStNode* p;
    if(s->next==NULL) return false;
    p = s->next;
    e = p->data;
    s->next = p->next;
    free(p);
    return true; 
}

取栈顶元素 GetTop(s, &e)

首先检查栈是否为空。

bool GetTop(LinkStNode *s, ElemType &e){
    if(s->next==NULL) return false;
    e = s->next->data;
    return true;
}

应用：设计及一个算法判断输入的表达式中的括号是否配对（假设只含有左、右圆括号）。

#include 
using namespace std;
typedef int ElemType;
typedef struct linknode {
	ElemType data;
	struct linknode* next;
}LinkStNode;
void initStack(LinkStNode* &s) {
	s = (LinkStNode*)malloc(sizeof(LinkStNode));
	s->next = NULL;
}
void Push(LinkStNode* &s, ElemType e) {
	LinkStNode *p;
	p = (LinkStNode*)malloc(sizeof(LinkStNode));
	p->data = e;
	p->next = s->next;
	s->next = p;
}
bool Pop(LinkStNode* &s) {
	LinkStNode* p;
	if (s->next == NULL) return false;
	p = s->next;
	s->next = p->next;
	free(p);
	return true;
}
bool StackEmpty(LinkStNode *s) {
	return s->next == NULL;
}
bool Match(char a[], int n) {
	LinkStNode* st;
	initStack(st);
	for (int i = 0; i < n; i++) {
		if (a[i] == '(') Push(st, a[i]);
		else if (a[i] == ')') Pop(st);
	}
	if (StackEmpty(st)) return true;
	else return false;
}
int main() {
	char a1[] = "((3+1)/3+2)7*(5-3)1";
	char a2[] = "(12-3)*(3*(5+4)";
	cout << Match(a1, 18) << endl;
	cout << Match(a2, 15) << endl;

	system("pause");	
}

队列（Queue，FIFO）

队列仅允许在表的一端进行插入操作，而在表的另一端进行删除操作。

队尾(rear)：进行插入的一端。

队首或队头(front)：进行删除的一端。

进队或入队(enqueue)：向队列中插入新元素，新元素进队后就成为新的队尾元素。

出队或离队(dequeue)：从队列中删除元素，元素出队后，其直接后继元素就成为队首元素。

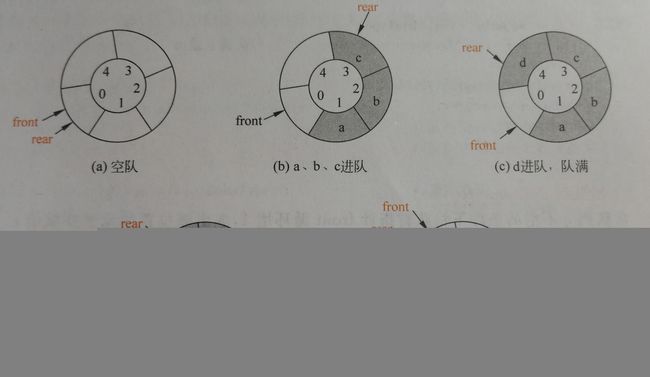
队空的条件：q->front == q->rear;

队满的条件：q->front == MaxSize - 1;                                                         //如图(b)、(c)

元素e进队操作：先将rear增1，然后将元素e放在data数组的rear位置；

出队操作：先将front增1，然后取出data数组中front位置的元素。

顺序队(sequential queue)及其基本运算的实现

顺序队的声明

#define MaxSize 50
typedef struct{
    ELemType data[MaxSize];
    int front, rear;
}SqQueue;

初始化队列 initQueue(&q)

构造一个空队列q，将front和rear均设置为-1

void initQueue(SqQueue* &q){
    q = (SqQueue*)malloc(sizeof(SqQueue));
    q->front = -1;
    q->rear = -1;
}

销毁队列 DestroyQueue(&q)

释放队列q占用的存储空间

void DestroyQueue(SqQueue* &q){
    free(q);
}

判断队列是否为空 QueueEmpty(q)

队空条件：q->front = q->rear;

bool QueueEmpty(SqQueue* q){
    return q->front==q->rear;
}

 进队列 enQueue(&q, e)

首先判断队列是否已满

bool enQueue(SqQueue* &q, ElemType e){
    if(q->rear==MaxSize-1) return false;
    q->rear++;
    q->data[q->rear] = e;
    return true;
}

出队列 deQueue(&q, &e)

首先判断队列是否为空

bool deQueue(SqQueue* &q, ElemType &e){
    if(q->front==q->rear) return false;
    q->front++;
    e = q->data[q->front];
    return true;
}

环形队列（或循环队列，circular queue)及其基本运算的实现

可以避免假溢出(false overflow)。

环形队列首尾相连后，当队尾指针 rear = MaxSize - 1后，在前进一个位置就到达0，于是就可以使用另一端的空位置存放队列元素。

循环队列初始时设置：front = rear = 0

循环队列队满和队空的条件都是 q->rear == q->front，因此不能因此区分。则将队满条件改为“队尾指针循环增1时等于队头指针”。这样，环形队列就要少用一个元素空间，即该队列中在任何时刻最多只能有MaxSize-1个元素。

队空条件：q->rear == q->front;

队满的条件：(q->rear + 1)%MaxSize == q->front;

进队时，队尾指针rear循环增1：rear = (rear + 1)%MaxSize;

出队时，队头指针front循环增1：front = (front + 1)%MaxSize;

初始化队列 InitQueue(&q)

构造一个空队列q，将front和rear指针均设置为初始状态，即为0

void InitQueue(SqQueue* &q){
    q = (SqQueue*)malloc(sizeof(SqQueue));
    q->rear = 0;
    q->front = 0;
}

销毁队列 DestroyQueue(&q)

释放队列q占用的存储空间

void DestroyQueue(SqQueue* &q){
    free(q);
}

判断队列是否为空 QueueEmpty(q)

队列为空条件为 q->front == q->rear;

bool QueueEmpty(SqQueue* q){
    return q->front==q->rear;
}

进队列 enQueue(&q, e)

首先判断队列是否已满

bool enQueue(SqQueue* &q, ELemType e){
    if((q->rear+1)%MaxSize==q->front) return false;
    q->rear = (q->rear+1)%MaxSize;
    q->data[q->rear] = e;
    return true;
}

出队列 deQueue(&q, &e)

首先判断队列是否为空

bool deQueue(SqQueue* &q, ElemType &e){
    if(q->front==q->rear) return false;
    q->front = (q->front+1)%MaxSize;
    e = q->data[q->front];
    return true;
}

用队列中元素个数代替队尾指针的环形队列及其基本运算的实现

对于环形队列来说，如果知道队头指针和队列中的元素个数，则可以计算出队尾指针。

初始时，qu->front = 0; qu->count = 0;

队空的条件：qu->count == 0;

队满的条件：qu->count == MaxSize;                               //因为不是通过qu->front与qu->rear的关系判断队空和队满

// 所以不存在因两种判断条件相同而需要少存储一个元素的情况，因此队满时 qu->count == MaxSize

进队操作：首先根据队首指针和元素个数求出队尾指针rear，将rear循环增1，然后将元素e放在rear处

出队操作：先将队首指针front 循环增1，然后取出该位置的元素

该环形队列最多可以放置MaxSize个元素

 该环形队列的结构体声明

#define MaxSize 50
typedef int ElemType;

typedef struct {
	ElemType data[MaxSize];
	int front;
	int count;
}QuType;

初始化该环形队列 InitQueue(&qu)

void InitQueue(QuType* &qu) {
	qu = (QuType*)malloc(sizeof(QuType));
	qu->front = 0;
	qu->count = 0;
}

进队操作 EnQueue(&qu, e)

bool EnQueue(QuType* &qu, ElemType e) {
	int rear;
	if (qu->count == MaxSize) return false;
	rear = (qu->front + qu->count) % MaxSize;
	rear = (rear + 1) % MaxSize;
	qu->data[rear] = e;
	qu->count++;
	return true;
}

出队操作 DeQueue(&qu, &e)

bool DeQueue(QuType* &qu, ElemType &e) {
	if (qu->count == 0) return false;
	qu->front = (qu->front + 1) % MaxSize;
	e = qu->data[qu->front];
	qu->count--;
	return true;
}

判断队列是否为空 QueueEmpty(qu)

bool QueueEmpty(QuType* qu) {
	return qu->count == 0;
}

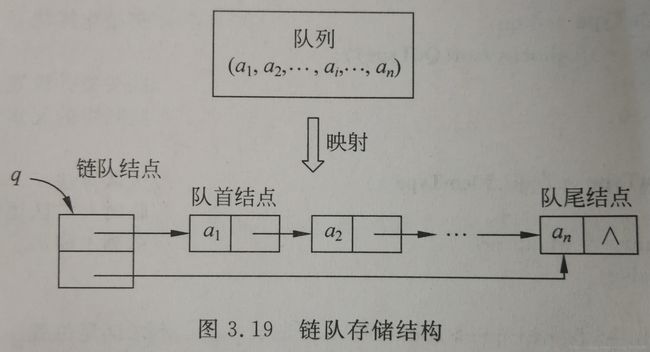
链队(linked queue)及其基本运算的实现

只允许在链表的表头进行出队操作，在表尾进行入操作，因此需要使用队头指针front和队尾指针rear，用front指向队首结点，用rear指向队尾结点。

初始时，q->front = NULL; q->rear = NULL;

队空的条件：q->rear == NULL (或 q->front == NULL)                       //只有一个数据结点时，也 q->front == q->rear;

进队操作：新建一个结点存放元素e（由p指向它），将结点p插入作为尾结点

出队操作：取出队首结点的data值，并将其删除

链队中数据结点的类型DataNode声明

typedef struct qnode{						
	ElemType data;
	struct qnode* next;
}DataNode;

链队头结点(或链队结点)的类型LinkQuNode声明

typedef struct{
	DataNode* front;
	DataNode* rear;
}LinkQuNode;

初始化队列 InitQueue(&q)

创建一个链队结点，其front和rear域均置为NULL。

void InitQueue(LinkQuNode* &q) {
	q = (LinkQuNode*)malloc(sizeof(LinkQuNode));
	q->front = NULL;
	q->rear = NULL;
}

销毁队列 DestroyQueue(&q)

释放链队占用的全部存储空间，包括链队结点和所有数据结点的存储空间。

void DestroyQueue(LinkQuNode* &q) {
	DataNode *pre, *p;
	pre = q->front;
	if (pre != NULL) {				//释放所有数据结点内存
		while (pre->next != NULL) {
			p = pre;
			pre = pre->next;
			free(p);
		}
		free(pre);
	}
	free(q);				//释放链队结点内存
}

判断队列是否为空 QueueEmpty(q)

不能用 q->front == q->rear 判断，因为大概链队中只有一个数据结点时，也有 q->front == q->rear。

bool QueueEmpty(LinkQuNode* q) {
	return q->rear == NULL;		   //或 return q->front == NULL;
}

进队列 enQueue(&q, e)

从队尾进队

void enQueue(LinkQuNode* &q, ElemType e) {		//从队尾进队
	DataNode* p;
	p = (DataNode*)malloc(sizeof(DataNode));
	p->data = e;
	p->next = NULL;
	if (q->rear == NULL)			//若原队列为空，则将q->front和q->rear都指向p
		q->front = q->rear = p;
	else
	{
		q->rear->next = p;		//先将当前尾结点(由q->rear指向)的next指向p
		q->rear = p;			//再将队尾指针q->rear指向p
	}
}

出队列 deQueue(q, e)

从队首出队

bool deQueue(LinkQuNode* &q, ElemType &e) {		 //从队首出队
	DataNode* t;
	if (q->front == NULL) return false;		 //若队空
	t = q->front;
	if (q->front == q->rear)			//原来只有一个数据结点时
		q->front = q->rear = NULL;
	else
		q->front = q->front->next;
	e = t->data;
	free(t);
	return true;
}

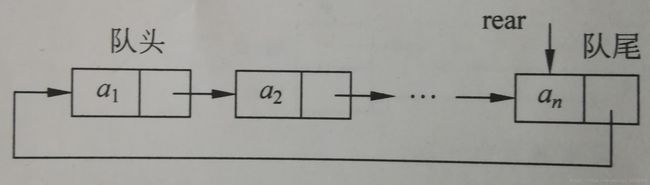
不带头结点只有一个尾结点指针rear的循环单链表实现的链队及其基本运算的实现

初始时，创建一个LinkNode类型结点rear，用来指向队尾数据结点。

队空的条件：rear == NULL;

进队操作：判断原队列是否为空/是否只有一个数据结点，新建一个结点存放元素e(由p指向它)，将结点p插入作为为尾结点，p->next指向原队列队首结点，让rear指向新结点p。

出队操作：判断原队列是否为空/是否只有一个数据节点，取出队首结点(rear所指结点的后继结点)的data值并将其删除。

数据结点类型的声明（同单链表）

typedef int ElemType;

typedef struct LNode{				//同单链表的数据结点类型声明
	ElemType data;
	struct LNode* next;
}LinkNode;

初始化 initQueue(&rear)

void initQueue(LinkNode* &rear) {
	rear = NULL;
}

判断队列是否为空 queueEmpty(rear)

bool queueEmpty(LinkNode* rear) {
	return rear == NULL;
}

进队操作 enQueue(&rear, e)

void enQueue(LinkNode* &rear, ElemType e) {
	LinkNode* p;
	p = (LinkNode*)malloc(sizeof(LinkNode));
	p->data = e;
	if (rear == NULL) {            //若原队列为空，插入后首尾相接
		p->next = p;
		rear = p;
	}
	else {                            //若原队列不为空
		p->next = rear->next;
		rear->next = p;
		rear = p;
	}
}

出队操作 deQueue(&rear, &e)

bool deQueue(LinkNode* &rear, ElemType &e) {
	LinkNode* t;
	if (rear == NULL) return false;            //若原队列为空
	if (rear == rear->next) {            //若原队列只有一个数据结点，将其删除后rear置为NULL
		e = rear->data;
		free(rear);
		rear = NULL;
	}
	else                        //若原队列有两个及以上数据结点
	{
		t = rear->next;
		e = t->data;
		rear->next = t->next;
		free(t);
	}
	return true;
}