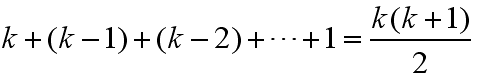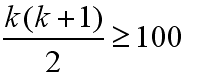N个鸡蛋从M楼层摔(2个鸡蛋从100层摔)
转载自: http://blog.csdn.net/wolinxuebin/article/details/47057707
http://www.cnblogs.com/yangai/p/5391533.html
一、题目:
有一栋楼共100层,一个鸡蛋从第N层及以上的楼层落下来会摔破, 在第N层以下的楼层落下不会摔破。给你2个鸡蛋,设计方案找出N,并且保证在最坏情况下, 最小化鸡蛋下落的次数。
二、思路:
先假设,最小的次数为x次。
首先在x层摔,那么会出现两个结果:
1、碎了,为了找出那一层碎了,第二个鸡蛋必须从1~x-1进行遍历的摔
2、没碎,那么第二次就在x+(x-1)楼层摔。
为什么是x+x-1楼层呢?
首先我们已经假设了通过x步我们就能得到答案,现在我们在x层已经用了一次了,那么就只剩下x-1步了。所以我们选择x+(x-1)层,如果碎了,我们就能通过x-2步,遍历x+1~x+(x-1)-1的所有楼层。
3、如果在x+(x-1)楼碎了,那么同1,遍历x+1~x+(x-1)-1
4、没碎,那么同2,就在x+(x-1)+(x-2)层摔
…
最后我们将会得出这样一个楼层公式x+(x-1)+(x-2)+…+1 = x(x+1)/2。
这个公式有什么意义呢?
有, x(x+1)/2 >= 100,这样才能顺利的解除x。
有人说,x(x+1)/2 = 99就可以,如果鸡蛋在99层都没碎,那么必定是100层。 我想说谁告诉你记得一定会碎!
那么我们就顺利的解除 x=14。
三、扩展
此题还有一个扩展,就是为N个鸡蛋从M层摔找出最小值。
那就不是很好手解了,所以写了代码,使用动态规划原理。动态规划式子如下:
f[n][m] = 1+max(f[n-1][k-1],f[n][m-k]) k属于[1,m-1]
解释下原理:
1、当手里有n个的时候,鸡蛋从k层往下摔,如果破了,那么手里只有n-1鸡蛋了,那么就需要测试f[n-1][k-1]楼层。或者更通俗好理解点的,我们运用2个鸡蛋100楼层的题目举例子。以上式子变为:f[2][m] = 1+max(f[1][k-1],f[2][m-k])
那么当手里有2个鸡蛋的时候,在k层摔,碎了。那么现在手里也就只有一个鸡蛋了,此时我们必须遍历1~k-1找出第一次碎的楼层。所以为1+f[1][m-k],前面的1代表在k层的操作。
2、没破,那么手里还有n个鸡蛋,那么需要测试k+1~m这些楼层。此时我想问下,当手里有2个鸡蛋测试1~m-k层和手里有2个鸡蛋测试k+1~m有什么区别?
有人说有,因为楼层越高越容易碎,那其实是你个人的想法罢了。其实并没有区别,所以第一个公式可以写为f[n][m-k]。
最后附上代码,为了理解方便,而不必从数组从0开始而困扰,这里就空间多开了点,所以如果拿去用的话,可以优化下:
public class Eggs{
public int countMinSetp(int egg,int num){
if(egg < 1 || num < 1) return 0;
int[][] f = new int[egg+1][num+1];//代表egg个鸡蛋,从num楼层冷下来所需的最小的次数
for(int i=1;i<=egg; i++){
for(int j=1; j<=num; j++)
f[i][j] = j;//初始化,最坏的步数
}
for(int n=2; n<=egg; n++){
for(int m=1; m<=num; m++){
for(int k=1; k//这里的DP的递推公式为f[n][m] = 1+max(f[n-1][k-1],f[n][m-k]) k属于[1,m-1]
//从1-m层中随机抽出来一层k
//如果第一个鸡蛋在k层碎了,那么我们将测试1~k-1层,就可以找出来,也即1+f[1][k-1]
//如果第一个鸡蛋在k层没有碎,那么我们将测试k+1~m也即m-k层,
// 这里也是重点!!!!
// 现在我们手里有2个鸡蛋,要测试m-k层,那么我想问,此时和你手里有2个鸡蛋要测试1~m-k层有什么区别?
// 没有区别!是的在已知k层不碎的情况下,测试k+1~m层的方法和测试1~m-k没区别,所以可以写成 1+f[n][m-k] 其中1表示为 在k层的那一次测试
f[n][m] = Math.min(f[n][m],1+Math.max(f[n-1][k-1],f[n][m-k]));
}
}
}
return f[egg][num];
}
public static void main(String[] args) {
Eggs e = new Eggs();
System.out.println(e.countMinSetp(2,100));
}
} - 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
参考文章:
100层楼2个鸡蛋,如何得知鸡蛋能承受几层的撞击
两个鸡蛋100层楼(DP)
有一栋楼共100层,一个鸡蛋从第N层及以上的楼层落下来会摔破, 在第N层以下的楼层落下不会摔破。给你2个鸡蛋,设计方案找出N,并且保证在最坏情况下, 最小化鸡蛋下落的次数。
我们先假设最坏情况下,鸡蛋下落次数为x,即我们为了找出N,一共用鸡蛋做了x次的实验。 那么,我们第一次应该在哪层楼往下扔鸡蛋呢?先让我们假设第一次是在第y层楼扔的鸡蛋, 如果第一个鸡蛋在第一次扔就碎了,我们就只剩下一个鸡蛋,要用它准确地找出N, 只能从第一层向上,一层一层的往上测试,直到它摔坏为止,答案就出来了。 由于第一个鸡蛋在第y层就摔破了, 所以最坏的情况是第二个鸡蛋要把第1到第y-1层的楼都测试一遍,最后得出结果, 噢,原来鸡蛋在第y-1层才能摔破(或是在第y-1层仍没摔破,答案就是第y层。) 这样一来测试次数是1+(y-1)=x,即第一次测试要在第x层。OK, 那如果第一次测试鸡蛋没摔破呢,那N肯定要比x大,要继续往上找,需要在哪一层扔呢? 我们可以模仿前面的操作,如果第一个鸡蛋在第二次测试中摔破了, 那么第二个鸡蛋的测试次数就只剩下x-2次了(第一个鸡蛋已经用了2次)。 这样一来,第二次扔鸡蛋的楼层和第一次扔鸡蛋的楼层之间就隔着x-2层。 我们再回过头来看一看,第一次扔鸡蛋的楼层在第x层,第1层到第x层间共x层; 第1次扔鸡蛋的楼层到第2次扔鸡蛋的楼层间共有x-1层(包含第2次扔鸡蛋的那一层), 同理继续往下,我们可以得出,第2次扔鸡蛋的楼层到第3次扔鸡蛋的楼层间共有x-2层, ……最后把这些互不包含的区间数加起来,应该大于等于总共的楼层数量100,即
x + (x-1) + (x-2) + ... + 1 >= 100 (x+1)*x/2 >= 100 得出答案是14。
即我先用第1个鸡蛋在以下序列表示的楼层数不断地向上测试,直到它摔破。 再用第2个鸡蛋从上一个没摔破的序列数的下一层开始,向上测试, 即可保证在最坏情况下也只需要测试14次,就能用2个鸡蛋找出从哪一层开始, 往下扔鸡蛋,鸡蛋就会摔破。
14, 27, 39, 50, 60, 69, 77, 84, 90, 95, 99, 100
比如,我第1个鸡蛋是在第77层摔破的,那么我第2个鸡蛋就从第70层开始,向上测试, 第二个鸡蛋最多只需要测试7次(70,71,72,73,74,75,76),加上第1个鸡蛋测试的 7次(14,27,39,50,60,69,77),最坏情况只需要测试14次即可得出答案。
这个问题还有一个泛化的版本,即d层楼,e个鸡蛋,然后设计方案找出N, 使最坏情况下测试的次数最少。这个要用动态规划(DP)来解。
f[d][e]表示d 层楼,e个鸡蛋时,最坏情况下的测试次数,则:
f[d][e]=min{max(f[d-i][e]+1,f[i-1][e-1]+1)},i=1,2,...,d;
f[k][1]=k,0<=k<=d,f[0][0...e]=0;
实现代码如下:
int min_testnumber(int d, int e)
{
int **f=new int *[d+1];
int i,j,k;
for(i=0;i<=d;i++)
f[i]=new int[e+1]; for(i=0;i<=d;i++) f[i][1]=i; for(i=0;i<=e;i++) f[0][e]=0; for(i=1;i<=e;i++) { for(j=1;j<=d;j++) { int tmp; int min_test=0x7FFFFFFF; for(k=1;k<=j;k++) { tmp=f[j-k][i]+1>f[k-1][i-1]+1?f[j-k][i]+1:f[k-1][i-1]+1; if(tmp>min_test) min_test=tmp; } f[j][i]=min_test; } } return f[d][e]; }
两个软硬程度一样但未知的鸡蛋,它们有可能都在一楼就摔碎,也可能从一百层楼摔下来没事。
有座100层的建筑,要你用这两个鸡蛋确定哪一层是鸡蛋可以安全落下的最高位置。可以摔碎两个鸡蛋。
最少需要几次测试,才能得到摔碎鸡蛋的楼层?方案如何?
=================================================
对于这个问题,如果从编程角度而言,最简单的思路是用动态规划的思想来解决,不过本文不将其从编程角度分析,而是从数学角度对问题进行论述。
================================================
对这个问题,原始问题——【100层楼,最少需要几次测试,才能得到摔碎鸡蛋的楼层】,直接考虑不容易考虑,但是,如果将这个问题进行一种等价的转换,这个问题将会变得非常容易解答。个人认为,这个转换是解决这个问题的核心,这个转换是:
转换问题——【两个鸡蛋,进行k次测试,最多可以测试几层楼】
如果大家能想到将“原始问题”变为“转换问题”,这个问题个人认为已经解决一半了,转换后,这个问题豁然开朗,思路全开。
现在我们以“转换问题”为模板进行考虑,有两个鸡蛋,第一个鸡蛋如果破碎,第二个鸡蛋就必须只能一层一层的测试了,而且,我们要求进行k次测试就将摔碎鸡蛋的楼层必须找到.
=====================================================
考虑第一次测试。第一次测试的时候,第一个鸡蛋不能放置的楼层太高了,否则,如果第一个鸡蛋破碎,第二个鸡蛋可能不能在k次测试后得到结果。但是也不能放置的矮了,因为如果放置的矮了,第一个鸡蛋破碎了还好说,如果没破,我们浪费了一次测试机会,也不能说是完全浪费了,不过至少是让效用没有最大化。所以,第一次测试的时候必须让第一个鸡蛋放置的不高不矮。
不高不矮是多高?高到如果第一个鸡蛋破碎后第二个鸡蛋刚好能完成k次测试得到结果这个目标。由此可知,第一次测试所在的楼层高度为k,如果第一次测试第一枚鸡蛋破碎,则剩下k-1层楼,一层一层的试,k次一定能完成目标。
如果第一次测试,第一枚鸡蛋没有破碎,则我们现在只有k-1次测试机会了,而且直到了k楼及其以下都是安全的了。我们消耗了一次测试机会,但是一次就测试了k层楼。
然后只有k-1次机会了,第二次测试,我们可以在k层的基础上再增加k-1层了,注意,这个时候由于我们只有k-1次机会,所以这次只能再增加k-1层,以保证测试的时候第一枚鸡蛋破碎的情况下仍然能完成任务。
于是,重复上述过程,直到最后一次机会,我们总共测试的楼层数为:
然后,再回到“原始问题”,100层楼,如果需要k次测试才能测试完成,则必须有
则可以得到,k≥14
也就是需要14次测试才能得到结果,而且这个过程也将测试方案一并得出来,就是第一次在14楼测试,如果第一枚蛋碎,则剩余13次机会,13层未知楼层,恰好,第二次在14+13=27楼测试,如此。
如果不是100层,而是N层,需要的测试次数为k,则有
=========================================================
然后,这个问题这个时候还可以扩展了,如果我们有三个鸡蛋,有k次机会,我们最大可以测试多少层楼?
思路同前面一样,第一次测试,不能太高也能太矮,必须恰到好处,也就是第一枚鸡蛋如果破碎,剩余k-1次机会能将剩余楼层给测试完。
由上面结论,k-1次机会最多可以测试k(k-1)/2层楼,所以第一次在k(k-1)/2+1层楼,第一次如果第一枚鸡蛋不碎,第二次在此基础上增加(k-1)(k-2)/2+1层楼,于是,三个鸡蛋k次机会总共测试楼层数为
k=9.
至于四个鸡蛋,五个鸡蛋,以至于M个鸡蛋,可以以此类推,方法同上。