笔试——编程&算法

1、子序列最大和

给定整数序列A1 A2….An,长度为n,其中整数可能为负数，现在要求A1~An的一个子序列Ai~Aj，使得Ai到Aj的和最大，并输出最大的和。

int MAXseq(const int a[], int n)
{
    int s1,s2,j;
    s1 = s2 = 0;

    for(j=0;j//s1记录累加和
        if(s1 > s2)
        {
            s2 = s1;
        }
        else if(s1 < 0)
        {
            s1 = 0;
        }
    }

    return s2;
}

2、求链表中间结点

最简单的想法：先遍历链表统计结点个数，然后结点数/2就是中间结点的位置，再遍历就可以指向中间结点
如果只能遍历一次呢？
优化算法：设定两个指向第一个结点的指针，一个(p)一次走一个，一个(q)一次走两个。当走的快的到达链表尾部（q->next==NULL ||q->next->next==NULL）时，慢的就指向中间结点。当然要特别考虑结点个数为0 1 2的情况。
REF: http://blog.csdn.net/dgglx/article/details/7486362

3、排序-折半插入排序

//折半插入排序
void Binary_insert_sort(node *a,int n)
{
    int i,j,head,tail,mid;
    node tmp;

    for(i=1;i
    {
        if(a[i].a < a[i-1].a)
        {
            copy(&tmp,a[i]);
            head = 0;
            tail = i-1;

            /*  mid的计算应该在tail/head改变之前计算
            **  避免当tail/head为负值的情况
            mid = (head + tail)/2;
            while(tail >= head)
            {
                if(tmp.a < a[mid].a)
                {
                    tail = mid -1;
                }
                else
                {
                    head = mid +1;
                }
                mid = (head + tail)/2;
            }
            */
            while(tail >= head)
            {
                mid = (head + tail)/2;  //mid可能为负数
                if(tmp.a < a[mid].a)
                {
                    tail = mid -1; //tail可能为负数
                }
                else
                {
                    head = mid +1;
                }
            }           
            //插入在**tail后**的位置(tail可能为负数)
            //for(j=i-1;j>tail;j--) 这种写法是错误的j>tail可能永远成立
            for(j=i-1;j>=**tail+1**;j--)
            {
                copy(a+j+1,a[j]);
            }
            copy(a+j+1,tmp);
        }
    }
}

4、二叉树-递归算法

求深度：

int BiTreeDepth(const BiTree t)
{
    int ld,rd;
    if(!t)
        return 0;   //递归退出的地方。
    ld = Depth(t->left);
    rd = Depth(t->right);

    return ld>rd?ld+1:rd+1; //树的深度为其左右子树的深度中最大者+1
}

5、计算1/0的位数，奇偶校验

奇偶校验：

unsigned int v;       // 待检测的数字
bool parity = false;  //初始判断标记
int num_of_1 = 0;
while (v)
{
  parity = !parity;
  v = v & (v - 1);
  num_of_1 ++;
}

v = v & (v - 1); 每执行一次，v中的1的个数减少一个。

REF: http://www.cnblogs.com/cpoint/p/3367375.html#top

6、周期串

如果一个字符串可以由某个长度为k的字符串重复多次得到，则该串以k为周期。例如，abcabcabcabc以3为周期（注意，它也以6和12为周期）。输入一个长度不超过80的串，输出它的最小周期。

样例输入：helpshelpshelpshelps
样例输出：5

#include 
#include 
#include 

void cycle_length(char *a,int length)
{
    int i,j;
    int flag;
    for (i=1;iif (length%i == 0)  //如果i为最小周期，那么字符串长度必定是i的整数倍
        {
            flag = 1;
            for (j=i;j//判断数组是否已i为周期
            {
                if (a[j-i] != a[j])
                {
                    flag = 0;
                }
                else 
                    break;
            }
            if (flag)
            {
                printf("%d \n",i); //输出对应的周期
                break; //如果flag不为0，那么退出循环
            }
        }
    }
}
//测试函数
void main()
{
    char *a="abcabcabc";
    cycle_length(a,strlen(a));

    system("pause");

}

7、走格子问题 非递归/递归实现

程序员面试宝典 P88
解法1：
我们可以把棋盘的左下角看做二维坐标的原点(0,0)，把棋盘的右上角看做二维坐标(M,N)(坐标系的单位长度为小方格的变长)
用f(i,j)表示移动到坐标f(i,j)的走法总数，其中0=

int process(int m, int n) 
{
    if (m == 0 && n == 0)
        return 0;
    if (m==0 || n==0)
        return 1;
    return process(m, n - 1) + process(m - 1, n);
}

int processNew(int m,int n){
    int **Q=new int*[m+1];
    for(int i=0; i<=m; ++i){
        Q[i]=new int[n+1]();
    }
    //初始化
    Q[0][0]=0;
    for(int j=1; j<=n; ++j)
        Q[0][j]=1;
    for(int i=1; i<=m; ++i)
        Q[i][0]=1;
    //迭代计算
    for(int i=1; i<=m; ++i){
        for(int j=1; j<=n; ++j){
            Q[i][j]=Q[i-1][j]+Q[i][j-1];
        }
    }
    int res=Q[m][n];
    delete [] Q;
    return res;
}

8、反转二进制位

C和指针 P89
例如在32位机器上，25为：
0000 0000 0000 0000 0000 0000 0001 1001
反转后为：
1001 1000 0000 0000 0000 0000 0000 0000
并且不能依赖于机器的整形长度。

unsigned int reverse_bits(unsigned int value)
{
    unsigned int i;
    unsigned int answer;  //返回的反转后的结果整形值。

    answer = 0;
    for(i = 1;i != 0;i <<= 1)  //当机器为N位时,此for循环将执行N次。
    {
        answer << 1;        //为下一个位留下空间，即将旧值移向高位。

        if(value & 1 == 1)  //若value的最低位，即当前处理位为1时
            answer |= 1;    //answer的最低位同样需要置1。

        value >> 1;         //当前位处理完成,移走之,进行下一位的处理。
    }

    return answer;
}

9、打印美元数据——字符串处理

C和指针 P191
输入 0 1 12 1234 123456789 分别打印出： 0.00 0.01 0.12 12.34 $1,234,567.89

void dollars(char *dest, char const *src)
{
    int len = strlen(src);
    int i;

    //处理符号
    *dest++ = '$';

    //处理小数点前面的数值
    if(len > 2)
    {
        for(i=len-2;i>0;)
        {
            *dest++ = *src++;
            if(--i && i%3 == 0)  //只有当能被3整除时才需要添加逗号
                *dest++ = ',';
        }
    }
    else
        *dest++ = '0';

    *dest++ = '.';
    //处理小数点后面的数值
    *dest++ = len < 2 ? '0':*src++;   //当len=1时，添加0 当len=2时，添加*src
    *dest++ = len < 1 ? '0':*src;     //当len=1时，添加*src 当len=2时，添加*src
    *dest = '\0';
}

10、输出后续遍历二叉树

《算法竞赛入门经典》 P106
题目：输入二叉树的先序遍历和中序遍历，输出其后续遍历。

//n为节点数，s1先序，s2中序，s后序
void build(int n, char *s1, char *s2, char *s)
{
    if(n <= 0)
        return;
    int root_idx = strchr(s2,s1[0]) - s2;  //根节点在中序遍历的位置

    build(root_idx, s1+1, s2+1, s);
    build(n - root_idx -1, s1+root_idx+1, s2+root_idx+1, s+root_idx);

    s[n-1] = s1[0];  //根节点放到最后
}

通过先序中序构造二叉树：
一个先序遍历序列和一个中序遍历序列可以确定一颗唯一的二叉树。
根据先序遍历的特点, 知先序序列(PreSequence)的首个元素(PreSequence[0])为二叉树的根(root), 然后在中序序列(InSequence)中查找此根(root), 根据中序遍历特点, 知在查找到的根(root) 前边的序列为根的左子树的中序遍历序列, 后边的序列为根的右子树的中序遍历序列。 设在中序遍历序列(InSequence)根前边有left个元素. 则在先序序列(PreSequence)中, 紧跟着根(root)的left个元素序列(即PreSequence[1…left]) 为根的左子树的先序遍历序列, 在后边的为根的右子树的先序遍历序列.而构造左子树问题其实跟构造整个二叉树问题一样，只是此时先序序列为PreSequence[1…left]), 中序序列为InSequence[0…left-1], 分别为原序列的子串, 构造右子树同样, 显然可以用递归方法解决。

自己编写的有错误的代码：

//DBACEGF ABCDEFG  先序中序建立二叉树
void build(BiTree **t, int n, char *pre, char *in)
{
    BiTree * q = *t;
    if(n <= 0)
        return;

    q = (BiTree *)malloc(sizeof(BiTree));
    if(!q)
        return;    
    q->s = pre[0];

    int root_idx;
    root_idx = strchr(in, pre[0]) - in;

    build(&(q->left), root_idx, pre+1, in);
    build(&(q->right), n-root_idx-1, pre+root_idx+1, in+root_idx+1);    
}

当用这段代码构造二叉树后，再遍历二叉树时会出现段错误，因为构造的二叉树没有分配内存。
这段代码错误的关键在于，先用q指向了*t，但是当分配内存后，q指向了另外一块内存，跟 *t或者说t没什么关系了，因此调用此函数后， *t所指向的二叉树根本就是空的。

修改为：

    BiTree * q;
    q = (BiTree *)malloc(sizeof(BiTree));
    if(!q)
        return;
    *t = q;//用q指向*t,或者不用定义q,直接使用*t处理。

11、二叉树中序遍历非递归算法

《数据结构算法解析》 P141 142
算法一：

void inorder_traverse(BiTree *t)
{
    BiTree stack[Q_LEN],*p;
    int top,btn;
    top = btn = 0;

    while(t || top != btn)  //二叉树不空或者栈不空时
    {
        if(t)  //二叉树不空,则根指针进栈,遍历左子树 
        {
            stack[top++] = t;
            t = t->left;
        }
        else  //二叉树为空,访问根节点遍历右子树
        {
            p = stack[--top];
            printf("%d ", p->index);
            t = t->right;
        }
    }
}

算法二：

void inorder_traverse2(BiTree *t)
{
    BiTree stack[Q_LEN],*p;
    int top,btn;
    top = btn = 0;

    stack[top++] = t;  //先入栈根指针

    while(top != btn)  //当栈不空时
    {
        while((p = stack[top-1]))  //取栈顶元素且自己和其左子树不空
            stack[top++] = p->left;  //向左走到尽头,入栈左孩子指针

        top--;  //弹出最后入栈的空指针。

        if(top != btn)
        {
            p = stack[--top];     //出栈并访问
            visit(p);
            stack[top++] = p->right;     //入栈右孩子指针
        }        
    }
}

以下为对算法二的改变：
不对任何空的指针进行入栈的操作。
中序遍历的操作是：左中右。
我们先把所有左孩子入栈。
然后在出栈一个节点，此时的节点就是最左边的孩子，访问之，而在它之前的栈中元素就是它的父节点，也可以访问之，此时左中都访问完毕；
再入栈右孩子，如此重复对右子树的操作。

void inorder_traverse2(BiTree *t)
{
    BiTree stack[Q_LEN],*p;
    int top,btn;
    top = btn = 0;

    stack[top++] = t;  //先入栈根指针

    while(top != btn)  //当栈不空时
    {
        while((p = stack[top-1]) && p->left != NULL)  //取栈顶元素且自己和其左子树不空
            stack[top++] = p->left;  //向左走到尽头,入栈左孩子指针

        while(top != btn)
        {
            p = stack[--top];     //出栈并访问
            visit(p);
            if(p->right)
            {
                stack[top++] = p->right;     //入栈右孩子指针
                break;
            }
        }        
    }
}

12、分数拆分

《算法竞赛入门经典》 P115
题目：
输入正整数k，找到所有的正整数x>=y，使得 1/k = 1/x + 1/y。
耗时大的代码：

void fraction()
{
    int k;
    scanf("%d",&k);
    int x,y,i,j;

    x=y=1;
    j = 2*k;
    while(x >= y)
    {
        for(y=1;y<=x&&y<=j;y++)
        {
            i=x*y;
            if(i%k == 0 && i/k == x+y)
            {
                printf("1/%d = 1/%d + 1/%d\n",k,x,y);
            }
        }
        x++;
    }   
}

此时x的循环非常大，而y<=2*k的结论是根据x>=y得来的，1/x <= 1/y => 1/x + 1/y <= 2/y。但是，我们可以根据k，y计算出x而不需要循环测试x。

void fraction()
{
    int k;
    scanf("%d",&k);

    int x,y,i,j;

    x=1;
    for(y=1;y<=2*k;y++)
    {
        j = k*y;
        i = y-k;
        if(i && j%i == 0)  //必须判断分母不为零。
        {
            x = j/i;
            if(x>=y)
            {
                printf("1/%d = 1/%d + 1/%d\n",k,x,y);
            }    
        }
    }      
}

13、十进制转n进制

//十进制a转换成n(2~10)进制数
void sys_trans(int a, int n, int *p, int *len)
{
    while(a)
    {
        *p++ = a%n;
        a /= n;
        tmp ++;
        (*len) ++;  //原来错误的写法为*len++，此时是取len所指的内容，然后丢弃，len往后移一位。
    }
}

14、 杨氏矩阵算法

杨氏矩阵：m行n列

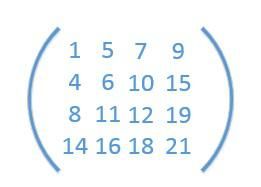
杨氏矩阵类似下面这个样子，行从左到右越来越小，列从上到下越来越大，让你找一个元素x,如何在O（n)时间内找到，n表示行列个数总和，如下，找9
10 6 4 2 0
12 7 6 3 1
13 8 7 5 2
这种情况下，可以从左上角开始比较，如果比x大，那么第一列都得去除，变成
6 4 2 0
7 6 3 1
8 7 5 2
接着从左上角比较，如果小，就把第一行去除，
7 6 3 1
8 7 5 2
再比较，比9小，去除第一行
8 7 5 2
再比较去除8，去除7，5，2
这样的话每次去除最多一行或者一列，时间复杂性是O(m+n)。

17、zigzag数组

《程序员面试宝典》 P92
ZigZag数组就是形如下图的，依次沿对角线增加->减小交替变换的数组

0 1 5 6 14 15 27 28
2 4 7 13 16 26 29 42
3 8 12 17 25 30 41 43
9 11 18 24 31 40 44 53
10 19 23 32 39 45 52 54
20 22 33 38 46 51 55 60
21 34 37 47 50 56 59 61
35 36 48 49 57 58 62 63

18、螺旋队列问题

《程序员面试宝典》 P95
设1的坐标是（0，0），x方向向右为正，y方向向下为正，例如，7的坐标为（-1，-1），2的坐标为（1，0）。编程实现输入任意一点坐标（x，y），输出所对应的数字！

关键点：
1、第t层从(2t-1)²+1开始，1为第零层。
2、给定坐标(x,y)，可求得其所在的层次，t=max(|x|,|y|)

参考：http://blog.csdn.net/yhmhappy2006/article/details/2934435

19、蛇形矩阵

《程序员面试宝典》 P97

【思路】：领用前面方向的数是否为0来判断是否达到尽头。

void p_fun(int n)
{
    int i,j,tmp = 1,n2 = n*n;
    memset(za,0,100*100*sizeof(int));

    i=j=0;
    za[i][j] = tmp++;
    while(tmp <= n2)
    {
        while(j+11]) za[i][++j] = tmp++;  //j+11]没有越界错误，不会错误的去判断za[i][n]位置的数。
        while(i+11][j]) za[++i][j] = tmp++;
        while(j>0 && !za[i][j-1]) za[i][--j] = tmp++;
        while(i>0 && !za[i-1][j]) za[--i][j] = tmp++;
    }

    for(i=0;ifor(j=0;jprintf("%d ",za[i][j]);
        printf("\n");
    }

}

20、并查集算法

题目：ACM 畅通工程 http://acm.nyist.net/JudgeOnline/problem.php?pid=608
参考：http://blog.csdn.net/dellaserss/article/details/7724401

#define MAX_TOWN_NUM 1000
int pre[MAX_TOWN_NUM];

//找根节点(找自己的老大)
int find(int x)
{
    if(pre[x] == x)  //老大是自己
        return x;
    else
    {
        find(pre[x]);
    }
}

//将两点连到一个集合中
int join(int x, int y)
{
    int pre_x,pre_y;

    pre_x = find(x);
    pre_y = find(y);

    if(pre_x != pre_y)
    {
        pre[pre_x] = pre_y;   //把y的老大变成x的老大的老大
    }
}

//初始化并查集,让每个人都是自己一个人的集合,即每个人的老大是自己
void init(int n)
{
    int i;
    for(i=1; i<=n; ++i)
        pre[i] = i;
}

int main()
{
    int town_cnt,road_cnt,count;
    int x,y,i,j;
    int *tmp;

    scanf("%d",&town_cnt);
    while(town_cnt > 0)
    {
        init(town_cnt);
        tmp = (int*)malloc(sizeof(int)*(town_cnt+1));
        if(!tmp)
            continue;
        memset(tmp,0,town_cnt);
        count = 0;

        scanf("%d",&road_cnt);
        while(road_cnt--)
        {
            scanf("%d%d",&x,&y);
            join(x,y);
        }

        //加入人员进来后,进行【路径压缩】
        for(i=1;i<=town_cnt;++i)
        {
            j = find(pre[i]);  //找到i的老大
            if(tmp[j] == 0)
            {
                count++;
                tmp[j] = 1;
            }
        }        
        scanf("%d",&town_cnt);        
    }
}

21、itoa实现算法 integer to alphanumeric

char* itoa(int value, char* string, int radix);
将任意类型的数字转换为字符串 int radix 转换进制数，如2,8,10,16 进制等
int atoi(const char *nptr);
把字符串转换成整型数
【注意点】num是负数时，需要特殊处理负号。然后再进行进制转换，还需要逆置转换后的内容。

char* itoa(int num,char*str,int radix)
{   
    /*索引表*/
    char index[]="0123456789ABCDEFGHIJKLMNOPQRSTUVWXYZ";   //可求10进制向1~36进制的转换
    unsigned unum;
    int i=0,j,k;

    /*确定unum的值*/
    if(radix==10 && num<0)/*十进制负数*/
    {
        unum=(unsigned)-num;
        str[i++]='-';
    }
    else                /*其他情况*/
        unum=(unsigned)num;

    /*转换*/
    do
    {
        str[i++] = index[unum%(unsigned)radix];  //进制转换
        unum /= radix;
    }while(unum);

    str[i]='\0';

    /*逆序*/
    if(str[0] == '-')
        k=1;/*十进制负数*/
    else
        k=0;

    char temp;
    for(j=k;j<=(i-1)/2;j++)
    {
        temp=str[j];
        str[j]=str[i-1+k-j];
        str[i-1+k-j]=temp;
    }

    return str;
}

22、卡特兰数

公式：
令h(0)=1,h(1)=1，catalan数满足递推式：
h(n) = h(0)* h(n-1)+h(1)*h(n-2) + … + h(n-1)h(0) (n>=2)
h(n) = C(2n,n)/(n+1) (n=0,1,2,…)
应用：
出栈次序
1、一个栈(无穷大)的进栈序列为1，2，3，…，n，有多少个不同的出栈序列?
h(n)种。
2、买票找零：有2n个人排成一行进入剧场。入场费5元。其中只有n个人有一张5元钞票，另外n人只有10元钞票，剧院无其它钞票，问有多少中方法使得只要有10元的人买票，售票处就有5元的钞票找零？(将持5元者到达视作将5元入栈，持10元者到达视作使栈中某5元出栈)
3、给定N个节点，能构成多少种不同的二叉树？h(n)
实现

void catalan() //求卡特兰数
{
    int i, j, len, carry, temp;
    a[1][0] = b[1] = 1;
    len = 1;
    for(i = 2; i <= 100; i++)
    {
        for(j = 0; j < len; j++) //乘法
        a[i][j] = a[i-1][j]*(4*(i-1)+2);
        carry = 0;
        for(j = 0; j < len; j++) //处理相乘结果
        {
            temp = a[i][j] + carry;
            a[i][j] = temp % 10;
            carry = temp / 10;
        }
        while(carry) //进位处理
        {
            a[i][len++] = carry % 10;
            carry /= 10;
        }
        carry = 0;
        for(j = len-1; j >= 0; j--) //除法
        {
            temp = carry*10 + a[i][j];
            a[i][j] = temp/(i+1);
            carry = temp%(i+1);
        }
        while(!a[i][len-1]) //高位零处理
        len --;
        b[i] = len;
    }
}

23、扔玻璃球求最高楼层

题目：
某幢大楼有100层。你手里有两颗一模一样的玻璃珠。当你拿着玻璃珠在某一层往下扔的时候，一定会有两个结果，玻璃珠碎了或者没碎。这幢大楼有个临界楼层。低于它的楼层，往下扔玻璃珠，玻璃珠不会碎，等于或高于它的楼层，扔下玻璃珠，玻璃珠一定会碎。玻璃珠碎了就不能再扔。现在让你设计一种方式，使得在该方式下，最坏的情况扔的次数比其他任何方式最坏的次数都少。也就是设计一种最有效的方式。

首先，为了保存下一颗玻璃珠自己玩，就采用最笨的办法吧：从第一层开始试，每次增加一层，当哪一层扔下玻璃珠后碎掉了，也就知道了。不过最坏的情况扔的次数可能为100。
当然，为了这一颗玻璃珠代价也高了点，还是采取另外一种办法吧。随便挑一层，假如为N层，扔下去后，如果碎了，那就只能从第一层开始试了，最坏的情况可能为N。假如没碎，就一次增加一层继续扔吧，这时最坏的情况为100-N。也就是说，采用这种办法，最坏的情况为max{N, 100-N+1}。之所以要加一，是因为第一次是从第N层开始扔。
不过还是觉得不够好，运气好的话，挑到的N可能刚好是临界楼层，运气不好的话，要扔的次数还是很多。不过回过头看看第二种方式，有没有什么发现。假如没摔的话，不如不要一次增加一层继续扔吧，而是采取另外一种方式：把问题转换为100-N，在这里面找临界楼层，这样不就把问题转换成用递归的方式来解决吗？看下面：
假如结果都保存在F[101]这个数组里面，那么：
F[N]=100-N，
F[100]=min（max（1，1+F[N-1]），max（2，1+F[N-2]），……，max（N-1，1+F[1]））;
看出来了没有，其实最终就是利用动态规划来解决这个问题。
下面是自己随便写的C++代码：

#include  
using namespace std;  
int dp[101] = { 0 };  

void solve()  
{  
    int i , j , k;  
    for(i = 2 ; i < 101 ; ++i)  
    {  
        dp[i] = i;  
        for(j = 1 ; j < i ; ++j)  
        {  
            k = (j>=(1 + dp[i-j])) ? j : (1 + dp[i-j]);  
            if(dp[i] > k)  
                dp[i] = k;  
        }  
    }  
}    
int main(void)  
{  
    dp[0] = 0 , dp[1] = 1;  
    solve();  
    printf("%d\n",dp[100]);  
    return 0;  
}

输出结果为14。也就是说，最好的方式只要试14次就能够得出结果了。
答案是先从14楼开始抛第一次；如果没碎，再从27楼抛第二次；如果还没碎，再从39楼抛第三次；如果还没碎，再从50楼抛第四次；如此，每次间隔的楼层少一层。这样，任何一次抛棋子碎时，都能确保最多抛14次可以找出临界楼层。
证明如下：
1、第一次抛棋子的楼层：最优的选择必然是间隔最大的楼层。比如，第一次如果在m层抛下棋子，以后再抛棋子时两次楼层的间隔必然不大于m层（大家可以自己用反证法简单证明）
2、从第二次抛棋子的间隔楼层最优的选择必然比第一次间隔少一层，第三次的楼层间隔比第二次间隔少一层，如此，以后每次抛棋子楼层间隔比上一次间隔少一层。（大家不妨自己证明一下）
3、所以，设n是第一次抛棋子的最佳楼层，则n即为满足下列不等式的最小自然数：
不等式如下： 1+2+3+…+(n-1)+n >= 100
由上式可得出n=14
即最优的策略是先从第14层抛下，最多抛14次肯定能找出临界楼层。
REF: http://www.cnblogs.com/sooner/p/3252439.html

24、走台阶问题

题目：一个楼梯有50个台阶,每一步可以走一个台阶,也可以走两个台阶,请问走完这个楼梯共有多少种方法？
REF：http://blog.csdn.net/weiwangchao_/article/details/6880128