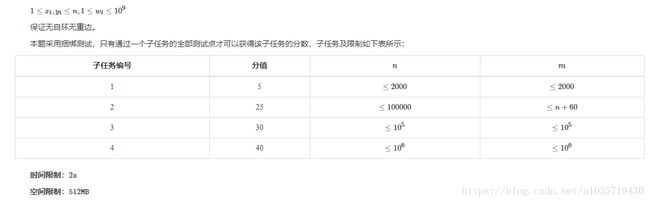
2018.7.30T2（lca+并查集+贪心）（另有主席树与LCT做法）

描述
蔡老板决定进军外卖行业。他刚刚高薪聘请了两位外卖小哥丁某和朱某，准备在 Q 城先做试点。

Q城一共有 n个节点组成，有 m 条街道连接这 n 个节点。对于第 i 条街道，它连接着 ui 和 vi 两个节点，并且有一个拥挤程度 wi。

如果蔡老板的外卖总部在第 x 号节点，那么每天两个外卖小哥需要从 x 点出发，经过这 nn 个点至少一次后再回到 x 号节点。他们可以经过一条边多次。但是如果他们没有在遍历完所有节点前经过了节点 x，那么他们就会被蔡老板认为是在偷懒而被扣工资。两个外卖小哥每次选择的方案会是在不被扣工资的前提下最小化经过的所有边的最大拥挤程度。

现在，两个外卖小哥想要知道，如果蔡老板的总部设在 i∈[1,n]中，他们所经过的所有边的最大拥挤程度最小值能是多少。但是他们并不会算，所以向你求助。特殊地，如果不能在遍历完所有节点之后再回到点 x ,我们认为点 x 的答案为-1。

为了减少输出时间，你只需要输出这 n 个数的和即可。

输入格式
第一行两个正整数 n,m。

第二行 m 个正整数 xi,yi,wi。

输出格式
你需要求出 n 个整数，第 i 个整数表示当蔡老板的总部设在点 i 时，他们所经过的所有边的最大拥挤程度最小值能是多少。特殊地，如果不能在遍历完所有节点之后再回到点 x，我们认为点 x 的答案为 −1。

为了减小输出量，你只需要输出它们的和。

样例1
input
5 6
1 3 3
1 2 2
2 3 5
2 4 2
3 4 4
3 5 1

output
13

---

对这题值得一提的是有LCA维护线段树以及主席树更新答案的两种做法

我们就来说说比较好写的做法

首先我们可以发现一个很显然的做法（5分）
去掉每个点其余点做最小生成树，答案就是每个最小生成树里面最小的边
当然也有一个原理相同的做法
从小到大加边，每次用 tarjan t a r j a n 判一下割点，每次从割点变为非割点，那则更新答案
到这里我们其实能想到30分的做法了。
我们肯定要等到整张图连通之后才会开始统计答案。
那我们先做一个最小生成树，一次加入其它的边即可算得答案。

考虑正解
我们考虑把所有点的答案放在一起统计
对于一个点，我们把他删掉，意味着最小生成树种的点会分成 di d i 个连通块
我们要做的就是选出一些非树边连接这些连通块并使花费最小
怎么统计答案？

一条边对一个点有连接连通块的贡献只有两种情况：
①这条边是连接这个点两个子树的边
②这条边从这个点的子树连到子树外
对于①我们发现这条边只会对他的LCA产生贡献

我们从小到大加入这些非树边，用并查集维护连通性，并更新LCA点对于的答案

那对于②呢？
对于除了LCA外的其它点它会把这个点的某个儿子连通块与父亲连通块连接起来，同时下次再有某条边要连接这两个连通块时我们就可以跳过了。（我们显然只会取小的这次）
那我们只要每次更新并查集并且更新①和②的答案就行了

因为每个连通块只会被合并一次，并且是用并查集
这一部分时间复杂度为 O(n) O ( n )

上述所有过程都可以用并查集来维护
故总时间复杂度为 O(nα(n)) O ( n α ( n ) )

AC代码：

#include
using namespace std;
#define maxn 1001000
#define ll long long
int n , m , linkk[maxn] , t , ola[4 * maxn] , cntw , mn[4 * maxn][30] , first[maxn];
int F[maxn] , mx_st , cnt;
int du[maxn] , has[maxn];
int dep[maxn] , f[maxn] , ans[maxn];
struct node{int n , y , x , v;}e[4 * maxn]; 
struct data{int x , y , v;}in[maxn],q[maxn];
int read()
{
    int sum = 0;char c = getchar();bool flag = true;
    while( c < '0' || c > '9' ) {if(c == '-') flag = false;c = getchar();}
    while( c >= '0' && c <= '9' ) sum = sum * 10 + c - 48 , c = getchar();
    if(flag)  return sum;
     else return -sum;
}  
void insert(int x,int y,int z)
{
    e[++t].y = y;e[t].x = x;e[t].n = linkk[x];e[t].v = z;linkk[x] = t;
    e[++t].y = x;e[t].x = y;e[t].n = linkk[y];e[t].v = z;linkk[y] = t;
    du[x]++;du[y]++;
    return;
}
bool mycmp(data a,data b){return a.v < b.v;}
int get(int x){return x == F[x] ? x : F[x] = get(F[x]);}
void dfs(int x,int fa)
{
    ola[++cntw] = x;first[x] = cntw;dep[x] = dep[fa] + 1;f[x] = fa;
    for(int i = linkk[x];i;i = e[i].n)
        if(e[i].y != fa)
        {
            int y = e[i].y;
            dfs(y , x);
            ola[++cntw] = x; 
        }
    return;
}
int Lca(int x,int y)
{
    if(first[y] < first[x]) swap(x,y);
    int k = log2(first[y] - first[x] + 1);
    return dep[ mn[first[x]][k] ] > dep[ mn[first[y] - (1<1][k] ] ? mn[first[y] - (1<1][k] : mn[first[x]][k];
}
void pre()
{
    dfs(1 , 0);
    for(int i = 1;i <= cntw;++i) mn[i][0] = ola[i];
    for(int j = 1;(1<for(int i = 1;i + (1<1];
            if(dep[ mn[ i + (1<<(j - 1)) ][j - 1] ] < dep[mn[i][j - 1]])
                mn[i][j] = mn[i + (1<<(j-1))][j-1];
        }
    return;
}
void change(int down,int up,int v)
{
    int now;down = get(down);now = f[down];
    while(dep[now] > dep[up])
    {
        ans[now] = v;
        has[now]++;
        F[down] = now;
        down = get(down);
        now = f[down];
    }
    return;
}
void solve()
{
    for(int i = 1;i <= cnt;++i)
    {
        int x = q[i].x , y = q[i].y , z = q[i].v;
        if(dep[x] > dep[y]) swap(x , y);
        int lca = Lca(x,y);
        change(y , lca , z);
        if(x == lca) continue;
        change(x , lca , z);   //返祖边更新
        x = get(x);y = get(y);
        if(dep[x] < dep[y]) swap(x,y);
        if(x != y) 
            F[F[x]] = F[y] , ans[lca] = z , has[lca]++;
    }
    return;
}
void work()
{
    n = read();m = read();
    for(int i = 1;i <= m;++i)
        in[i].x = read() , in[i].y = read() , in[i].v = read();
    sort(in + 1,in + m + 1,mycmp);
    for(int i = 1;i <= n;++i) F[i] = i;
    int sum = 0;
    for(int i = 1;i <= m;++i)
    {
        int x = in[i].x , y = in[i].y , z = in[i].v;
        if(get(x) != get(y)) F[F[x]] = F[y] , insert(x , y , z) , mx_st = z , sum++;
        else q[++cnt] = in[i];
    }
    if(sum < n - 1) {printf("%d\n",-n);exit(0);} 
    for(int i = 1;i <= n;++i) F[i] = i;
    pre();
    solve();
    return;
}
void print()
{
    ll sum = 0;
    for(int i = 1;i <= n;++i)
    {
        if(du[i] == 1) sum += mx_st;
        else if(has[i] >= du[i] - 1) sum += max(ans[i] , mx_st);
        else sum--;
    }
    printf("%lld",sum);
    return;
}
int main()
{
    work();
    print();
    return 0;
}