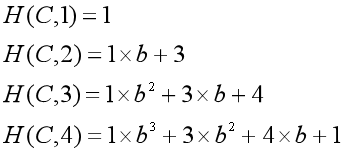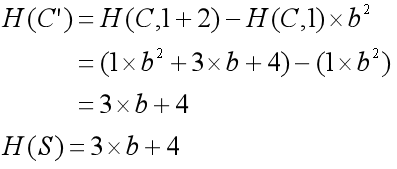介绍
哈希算法是通过一个哈希函数,将一段数据(也包括字符串、较大的数字等)转化为能够用变量表示或是直接就可作为数组下标的数字,这样转化后的数值我们称之为哈希值, 也就是算出一个数来代表一个字符串。
我们通过哈希值从而实现很快地查找和匹配,
常用:字符串Hash和哈希表。
字符串Hash流程
如果我们用O(m)的时间来计算长度为m的字符串的哈希值,则总的时间复杂度并没有改观,这里就需要用到一个叫做滚动哈希的优化技巧。
我们选取两个合适的互素常数b(进制)和h(模数)(b < h),假设字符串C =c1c2...cm,那么我们定义哈希函数:
正常的数字是十进制的,这里b是基数,相当于把字符串看做是b进制数。
这一过程是递推计算的,设H(c, k)为前k个字符的构成的字符串的哈希值,则:(以下均不考虑取模的情况)
如字符串C=“ACDA”(为方便处理,我们令‘A’表示1,‘B’表示2,以此类推),则:
通常题目要求的判断字符串C 从位置k+1开始的长度为n的子串C'=ck+1ck+2...ck+n的哈希值与另一匹配串S = s1s2...sn的哈希值是否相等,则:
于是只要预处理出bn,就能在O(1)时间内得到任意的字符串子串哈希值,从而完成字符串匹配,那么上述字符串匹配问题的总复杂度就为O(n + m)。
如字符串C=“ACDA”,S=”CD”,当k=1, n=2时:
因此子串C'与匹配串S匹配。
在实现时,可以利用64位无符号整数计算哈希值,即取h=2^64,通过自然溢出省去求模运算。
字符串Hash正确性
字符串Hash对于任意不同的字符串所产生的哈希值必然是互不相同的吗?显然不是的,但概率很低,在竞赛中我们常常认为这种情况不会发生。
即便如此,我们还可以再用“双哈希”降低出现相同哈希值的概率,即取不同的模数,把不同模数算出的哈希值都记下来,只有几个哈希值都一样,我们才能判定匹配。我们通常用双哈希就可以将冲突的概率降到很低,如果分别取h=10^9+7和h=10^9+9,就几乎不可能发生冲突,因为他们是一对“孪生素数”。
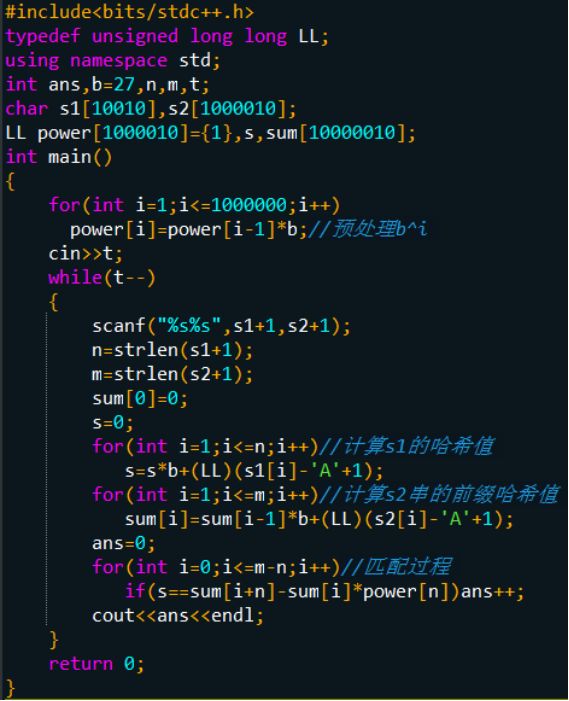
【例题1】Oulipo(信息学奥赛一本通 1455)
【题目描述】
给出两个字符串s1,s2((只有大写字母),求s1在s2中出现多少次。 例如:s1="ABA",s2="ABAABA",答案为2。
【输入】
输入T组数据,每组数据输出结果。
【输出】
如题述。
【输入样例】
3
BAPC
BAPC
AZA
AZAAZAAZA
VEEDI AVERDXIVYERDLAN
【输出样例】
1
3
0
哈希表流程
现在要存储和使用下面的线性表:A(1,75,324,43,1353,91,40)。
定义一个一维数组A[1...n],此时n=7,将表中元素按大小顺序存储在A[i]中,但这样就算使用二分查找,我们仍需要用O(log n)的时间去查找某个元素。
为了用O(1)的时间实现查找,可以开一个一维数组A[1...1353],使得A[key]=key,但显然造成了空间上的很大浪费,尤其是数据范围很大时。
为了使空间开销减少,我们可以对第二种方法加以优化,设计一个哈希函数H(key) = key mod 13,然后令A[H(key)]=key,这样一来定义一个一维数组A[0...12]就已足够,这种方法就是哈希表。
但刚才那样的存储是有问题的,如H(1)=H(40)=1,在存储40时又把1给覆盖掉了,那么查询就会出现错误,这种不同的数据产生相同哈希值的情况我们称之为冲突。
这里与字符串Hash有所不同,可能不论我们怎样选用哈希函数,还是很难避免产生冲突。
因此我们考虑对每一个哈希值记一个链表(其实也就相当于邻接表),把所有等于同一个哈希值的数字都存储下来,而查询只要遍历对应的链表即可,这样实际复杂度取决于查询的链表长度,也可以看做是常数级。
例如我们定义哈希函数H(x) = x mod 16,插入一些数据的效果如下图。
哈希函数的构造
通常情况下,我们用除余法来构造哈希函数。 ·即选择一个适当的正整数b,用其对取模的余数作为哈希值。
其关键是b的选取,为了尽量避免冲突,一般选为能够存储下并且尽量大的素数(一般情况下我们根据空间取10^6左右的素数)。一般地说,如果b的约数越多,那么冲突的几率就越大。
using namespace std;
const int N = 50000; //定义总共存入哈希表的数字个数
const int b = 999979; //定义哈希函数中的模数
int tot, adj[H], nxt[N], num[N]];
void insert(int key) //将一个数字插入哈希表
{
int h = key % b; //除余法
for (int e = adj[h]; e; e = nxt[e]) { if (num[e] == key) return ; }
//如果链表中已经出现过当前的数字就不用再存储一遍
nxt[++tot] = adj[h], adj[h] = tot;
num[tot] = key; //建立链表,存储下所有哈希值等于h的数字
}
bool query(int key) //查询数字x是否存在于哈希表中
{
int h = key % b; //同样先进行取余,求其哈希值
for (int e = adj[h]; e; e = nxt[e])
if (num[e] == key) return true; //查询对应链表,查询到则表示存在
return false; //不存在返回 false
}
}
【例题2】图书管理(信息学奥赛一本通 1456)
【题目描述】
图书管理是一件十分繁杂的工作,在一个图书馆中每天都会有许多新书加入。为了更方便的管理图书(以便于帮助想要借书的客人快速查找他们是否有他们所需要的书),我们需要设计一个图书查找系统。 该系统需要支持 2 种操作: add(s) 表示新加入一本书名为 s 的图书。 find(s) 表示查询是否存在一本书名为 s 的图书。
【输入】
第一行包括一个正整数 n,表示操作数。 以下 n 行,每行给出 2 种操作中的某一个指令条,指令格式为:add s 或 find s 在书名 s 与指令(add,find)之间有一个隔开,我们保证所有书名的长度都不超过 200。可以假设读入数据是准确无误的。
【输出】
对于每个 find(s) 指令,我们必须对应的输出一行 yes 或 no,表示当前所查询的书是否存在于图书馆内。 注意:一开始时图书馆内是没有一本图书的。并且,对于相同字母不同大小写的书名,我们认为它们是不同的。
【输入样例】
4
add Inside C#
find Effective Java
add Effective Java
find Effective Java
【输出样例】
no
yes