分别用拓扑排序和动态规划实现关键路径

关键路径：

所谓关键路径，就是例如工程的进展顺序问题，为了合理地安排和调度各活动，这样我们就可以用拓扑排序把每件事的先后顺序理出来。我们来看一个例子：

每个活动的最早完成时间就是直接相邻的之前活动中最晚的的最早完成时间加上二者持续时间。所谓机动时间就是在每个顶点的最晚完成时间与最早完成时间的差值，也就是这个工程因为其他工程的工期较长而目的地又相同，可以等一等再做。

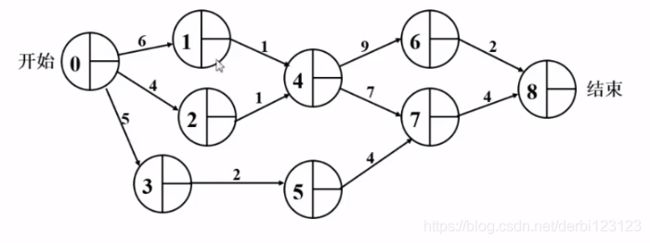
首先我们来看，这个工程图中在4、5处显然必须要4、5->7都完工后才能进行7->8，如果我们要求工期。显然我们必须等4、5中工期长的那个（4）都完工后才能继续进行，所以我们不妨让二者中最早完成时间短的顶点也有一条指向最早完成时间长的顶点的边，边权为0，来表示只有进行完工期长的才能继续。而每个顶点的最早完成时间就是前一个最晚顶点的最早完成时间加上两顶点间的时间，对于4、5这样需要都完成才能进行下一步的（7），7的最早完成时间应该都是二者间最早完成时间+持续时间大的那个。

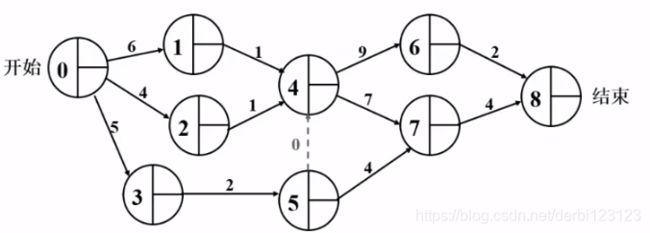
到此分析就结束了，下面是用两种方法实现的关键路径：

拓扑排序的实现方法

（1）实现拓扑排序得到工程顺序以及如何得到所有活动的最早完成时间

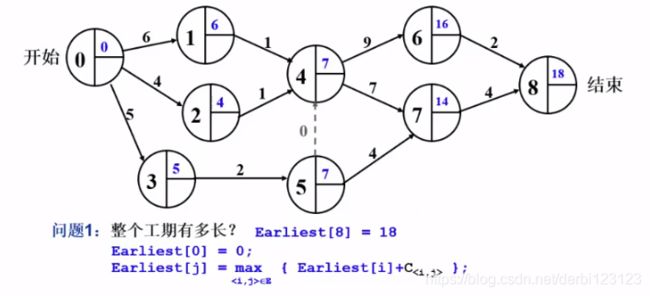
每个活动的最早完成时间就是之前直接相邻的活动中最晚的最早完成时间加上二者持续时间。根据图中的公式可以得到所有顶点的最早完成时间，最后一个顶点的最早完成时间就是整个工期的长度。 所以我们可以把这一步放到拓扑排序中完成：

#include 
#include 
#include 
#define maxn 1000
using namespace std;
struct node{
	int v;
	int weight;
};
vector<node> G[maxn];//邻接表表示图 
bool TopSort(int N)
{
	int Earliest[N]={0};//记录每个节点的最早完成时间
	queue<int> q;//存度为0的顶点的队列 
	stack<int> TopOrder;//存拓扑排序结果的序列
	
	int Indegree[N]={0},v,w;
	//遍历图得到每个顶点的入度 
	for(v=0;v<N;w++){
		for(w=0;w<G[v].size();w++){
			Indegree[G[v][w].v]++;
		}
	}
	//入度为0的顶点入队 
	for(v=0;v<N;v++){
		if(Indegree[v]==0){
			q.push(v);
		}
	}
	//入度为0的顶点出队 
	int cnt=0;//记录入队顶点个数 
	while(!q.empty()){
		int v=q.front();
		TopOrder[cnt++]=v;//放入结果序列 
		q.pop();
		//每次度为0的顶点出队后它指向的邻接点的度就会-1，如果-1后度为0就入队。 
		for(int w=0;w<G[v].size();w++){
			if(--Indegree[w]==0){
				q.push(w);
			} 
			if(Earliest[w]<Earliest[v]+G[v][w].weight){
				Earliest[w]=Earliest[v]+G[v][w].weight;
			}
		} 
	} 
	//如果不是所有顶点都入队，那么说明图不连通 
	if(cnt==N)
		return true;
	else
		return false;
}

（2）如何得到所有活动的最晚完成时间

最后一个活动的最早完成时间就是整个工期的长度也是其最晚完成时间。

注意最晚完成时间是倒着往回推。就是当前活动的最晚完成时间就等于所有后一活动的最晚完成时间减去二者间的持续时间中的最小值。

由于要倒着往回推，我们可以把上一步的结果数组改为栈存储，这样就可以利用栈先进后出的特点实现逆序输出。

//stack  TopOrder;假设上一步用的是栈存储结果序列
int Latest[n];
for(int i=0;i<n;i++)
	Latest[i]=Earlist[n-1];//每个节点的最晚完成时间都初始化为整个工程完成的最晚时间
while(!TopOrder.empty()){
	int v=TopOrder.top();
	TopOrder.pop();
	for(int w=0;w<G[v].size();w++){
		if(Latest[v]>Latest[w]-G[v][w].weight){
			Latest[v]=Latest[w]-G[v][w].weight;
		}
	}
}

（3）如何得到所有活动的机动时间和关键路径

再从0开始每次按公式计算完得到的绿色就是机动时间（可以拖延的时间）。所谓机动时间就是在每个顶点的最晚完成时间与最早完成时间的差值，也就是这个工程因为其他工程的工期较长而目的地又相同，可以等一等再做。


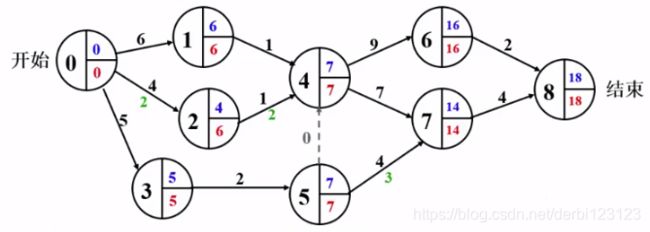
每个路径的机动时间也就是可以延误的时间，我们发现有些路径（活动、工程）是不能被耽误，也就是那些最早开始时间和最晚开始时间相同的活动（机动时间为0的活动），因为只要他们的工期延长就会导致整个工期延长，这些绝对不允许延误的活动组成的路径称为关键路径。 下面是求机动时间和关键路径的代码：

struct node{//为了便于表示机动时间，我们把它放入图的结构体中
	int v,weight,D;//D为机动时间
}
for(int v=0;v<n;v++){
	for(int w=0;w<G[v].size();w++){
		G[v][w].D=Latest[w]-Earliest[v]-G[v][w].weight;//得到机动时间
		if(G[v][w].D==0){
			cout<<v<<w;//输出关键路径
		}
	}
}

动态规划的实现方法

（1）求整个图中的最长路径：

也就是不固定起点和终点。
我们知道动态规划最重要的就是每一步的转换，也就是相邻顶点间的关系的表示。对于当前情况，我们可以让dp[i]表示从i号顶点出发能获得的最长路径，显然它和它的相邻顶点的关系是，dp[i]=max（dp[j]+G[i][j]），j可以有很多个故取最大值，当然是在i的所有相邻顶点的dp值都知道的前提下。
显然如果使用拓扑排序来解决，我们需要逆序的拓扑序列，因为要从没有出度的边界顶点开始往回推，但是如果用动态规划，要想实现这种逆序的想法，需要使用递归，先将问题分解到边界顶点，再开始运算。
这样我们就可以得到代码了：

int dp[maxn]={0};//从i号顶点出发能获得的最长路径初始化为0
int DP(int i)
{
	if(dp[i]>0) return dp[i];
	for(int j=0;j<n;j++){
		if(G[i][j]!=INF){
			dp[i]=max(dp[i],DP(j)+G[i][j]);//递归会在j是边界顶点时停止
		}
	}
	return dp[i];
}

如果我们还想得到具体的从i号顶点出发的最长路径，我们可以像求最短路径中的path数组一样，每一步都存上一步的顶点（前驱顶点），只不过在这里我们存的是下一步的顶点（后继顶点）：

int dp[maxn]={0};//从i号顶点出发能获得的最长路径初始化为0
int choice[maxn]={-1};
int DP(int i)
{
	if(dp[i]>0) return dp[i];
	for(int j=0;j<n;j++){
		if(G[i][j]!=INF){
			int tmp=DP(j)+G[i][j];
			if(dp[i]<tmp){
				dp[i]=tmp;
				choice[i]=j;//i的后继顶点是j
			}
		}
	}
	return dp[i];
}
//输出i的最长路径
void PrintPath(int i)
{
	cout<<i;
	while(choice[i]!=-1){
		i=choice[i];
		cout<<i;
	}
}

（2）求整个图中终点为T的最长路径：

现在不是所有顶点都可以到自己的路径为0了，因为了有了固定的终点，dp[i]表示的是i号顶点到T的最长路径，显然我们需要初始化dp[T]=0，而其他的顶点dp[i]=负的INF（自己想想为什么不能是负的），来表示无法到达终点。此外还需要一个visited数组来标识dp[i]是否被计算过，因为dp[i]的正负已经不能标识了（若i无法到达T则为-INF）。

bool visited[maxn]={false};
int DP(int i)
{
	if(visited[i]) return dp[i];
	visited[i]=true;
	for(int j=0;j<n;j++){
		if(G[i][j]!=INF){
			dp[i]=max(dp[i],DP(j)+G[i][j]);//递归会在j是边界顶点时停止
		}
	}
	return dp[i];
}

如果想得到i到T的具体最长路径还是和第一种情况一样，加一个存后继顶点的数组就行了

显然动态规划的写法要比拓扑排序容易多了，但是理解起来还是拓扑排序更加清晰。
下面来看一个经典的嵌套矩阵的例子：

对于这道题的实际应用，我们可以把每个矩形看做一个顶点，如果矩形i能嵌套于矩形j内，则j有一条指向i的路径，权值为1，不能嵌套的在初始化时就是0了，这样遍历矩阵序列，就能构成一个有向无环图，之后用最长路径的方式解决即可。那么有多条最长路径时怎样输出字典序最小的呢？ 其实在上面的代码中，我们已经是按照邻接点从小到大的顺序在遍历了，所以这个问题其实自动解决了。