数据结构与算法｜最小生成树算法（普里姆算法、克鲁斯卡尔算法）

最小生成树算法

C语言代码部分来自小甲鱼的《数据结构与算法》

最小生成树：一个有 n 个结点的连通图的生成树是原图的 极小连通子图，且包含原图中的所有 n 个结点，并且有保持图连通的最少的边。

​ 最小生成树可以用kruskal（克鲁斯卡尔）算法或prim（普里姆）算法求出，它们考虑问题的出发点是：为使生成树上边的权值之和达到最小，则应使生成树中每一条边的权值尽可能的小。

​ 普里姆算法是以某个顶点为起点，逐步找到每个顶点上最小权值的边来构建最小生成树。克鲁斯卡尔算法则换一种思路，从边出发，因为权值是在边上，所以直接去找最小权值的边来构建生成树。

区别：当边较多顶点较少时，用普里姆算法比较快；当边较少顶点较多时，用克鲁斯卡尔算法比较有优势

一、普里姆(Prim)算法

​

1.C语言代码

#include "math.h"
#include "stdio.h"

#define MAXVEX 50


typedef struct MGraph
{
    char vex[MAXVEX];       // 顶点集合
    int numVertexes;           // 顶点数
    int numedg;           // 边数
    int arc[MAXVEX][MAXVEX]; // 邻接矩阵
}MGraph;
//=============================================//
//=============================================//


//Prim算法生成最小生成树
void MiniSpanTree_Prim(MGraph G)
{
    int min,i,j,k;
    int adjvex[MAXVEX]; //保存相关顶点下标
    int lowcost[MAXVEX]; //保存相关顶点间边的权值

    lowcost[0]=0;       //V0作为最小生成树的根开始遍历，权值为0（当走到哪里时，显示所有联结的边）
    adjvex[0]=0;        //V0第一个加入(这是路径)

    //初始化操作
    for(i=1;i<G.numVertexes;i++)
    {
        lowcost[i]=G.arc[0][i];  //将邻接矩阵第0行所有权值先加入数组
        adjvex[i]=0;             //初始化全部先为V0的下标
    }


    //真正构造最小生成树的过程
    for(i=1;i<G.numVertexes;i++)
    {
        min=INFINITY;  //初始化最小权值为不可能数值inf
        j=1;
        k=0;

        //遍历全部顶点
        while (j<G.numVertexes)
        {
            //找出lowcaost数组已存储的最小权值（查找最小可走边）
            if(lowcost[j]!=0 && lowcost[j]<min)
            {
                min=lowcost[j];
                k=j;        //将发现的最小权值的下标存入k，以待使用。
            }
            j++;
        }

        //打印当前顶点边权值最小的边
        printf("(%d,%d)",adjvex[k],k);  //adjvex是路径
        lowcost[k]=0;  //将当前顶点的权值设置为0，表示此顶点已经完成任务，进行下一个顶点的遍历

        //邻接矩阵k行逐个遍历全部顶点
        for(j=1;j<G.numVertexes;j++)
        {
            if(lowcost!=0 && G.arc[k][j]<lowcost[j])
            {
                lowcost[j]=G.arc[k][j];
                adjvex[j]=k;
            }
        }

    }
}

2.算法思路

1. 定义lowcost[i]为**“当前”**最小生成树所能达到图中（非“当前”最小生成树中的）第i个顶点的最小权值；定义 adjvex[i]为“当前”最小生成树中第i个顶点与的第adjvex[i]个顶点相连接。
2. 初始化：设置“当前”最小生成树仅包括第一个顶点，lowcost[i]设为之该顶点到图中顶点的距离；adjvex[i]=0，因为此时“当前”最小生成树中仅有一个顶点。
3. 循环（不包括第一个顶点，因为第一个顶点已经在初始化中包含在了最小生成树中）：从lowcost[i]中选出最小非零权值，并将相应的该顶点加入最小生成树，输出并更新lowcost数组和adjvex数组。

---

二、克鲁斯卡尔(Kruskal)算法

1.C语言代码

#include "math.h"
#include "stdio.h"

#define MAXVEX 50
#define MAGEDGE MAXVEX*MAXVEX/2

typedef struct Edge
{
    int begin;//边的起点
    int end;//边的终点
    int weight;//边的权值

}Edge;    //权值非0的边的存储结构

typedef struct MGraph
{
    char vex[MAXVEX];       // 顶点集合
    int numVertexes;           // 顶点数
    int numEdges;           // 边数
    int arc[MAXVEX][MAXVEX]; // 邻接矩阵
}MGraph;


//Kruskal算法生成最小生成树
int Find(int *parent, int f)  //若f在"当前"最小生成树中，则f顺位至生成树的叶结点
{
    while(parent[f] > 0)
    {
        f=parent[f];
    }
    return f;
}

void MiniSpanTree_Kruskal(MGraph G)
{
    int i,n,m;
    Edge edges[MAGEDGE];  //定义边集数组
    int parent[MAXVEX];   //定义parent数组用来判断边与边是否形成环路

    //初始化
    for(i=0;i< G.numVertexes;i++)
    {
        parent[i]=0;
    }

    for(i=0;i<G.numEdges;i++)
    {
        n=Find(parent,edges[i].begin);
        m=Find(parent,edges[i].end);

        if(n!=m)    //如果n==m，则形成环路，不满足！
        {
            //将此边的结尾顶点放入下标为起点的parent数组中，表示此顶点已经在生成树集合中
            parent[n]=m;   //"当前"最小生成树中，叶结点m的父母为n，
            printf("(%d,%d) %d",edges[i].begin,edges[i].end,edges[i].weight);
        }
    }
}

2.算法思路

宗旨

在形成最小生成树的过程中：新添边相应的（在树中的）结点仅仅可能是叶结点与叶结点、叶结点与孤立结点、孤立结点与孤立结点

在建立最小生成树时，不断向“当前”最小生成树中添加新边，添加顺序按照边的权值从小到大排列：

• 若添加的边相应的顶点都不在树中，则直接添加；

• 若添加的边的仅有一个相应的顶点是在树中的结点，则通过Find不断寻找该结点在树中的孩子而得到的叶结点，与另一个结点（孤立顶点）相连；

• 若添加的边相应的顶点都是树中的结点，且通过Find函数不断寻找树中这两个结点在树中的孩子，而顺位到叶结点时，这两个结点相等，则不添加（若添加会形成环），若不相等，则添加。

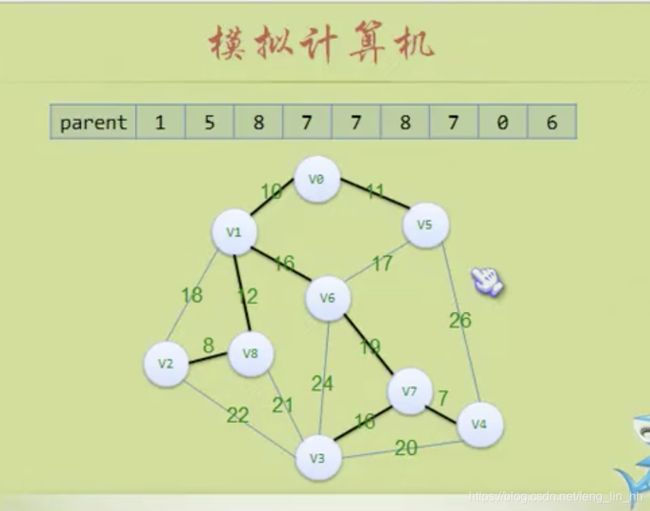
#根据上图的例子所进行的演示
              parent数组
              0 1 2 3 4 5 6 7 8
              -----------------
 1.初始化      0|0|0|0|0|0|0|0|0
 
 2.对每一条边的顶点运行Find函数，并更新parent数组
              -----------------
(4,7)->(4,7)  0|0|0|0|7|0|0|0|0   #孤立结点与孤立结点之间的边（经过Find函数后不变）
              -----------------
(2,8)->(2,8)  0|0|8|0|7|0|0|0|0
              -----------------
(0,1)->(0,1)  1|0|8|0|7|0|0|0|0
              -----------------
(0,5)->(1,5)  1|5|8|0|7|0|0|0|0  
              -----------------
(1,8)->(5,8)  1|5|8|0|7|8|0|0|0
              -----------------
(3,7)->(3,7)  1|5|8|7|7|8|0|0|0   #叶结点与孤立结点之间的边（经过Find函数后不变）
              -----------------
(1,6)->(8,6)  1|5|8|7|7|8|0|0|6
              -----------------
(5,6)->(6,6)  1|5|8|7|7|8|0|0|6
              -----------------
(1,2)->(6,6)  1|5|8|7|7|8|0|0|6
              -----------------
(6,7)->(6,7)  1|5|8|7|7|8|7|0|6   #此时是两个叶结点相连接（经过Find函数后不变）
              -----------------
(3,4)->(7,7)  1|5|8|7|7|8|7|0|6
              -----------------
(3,8)->(7,7)  1|5|8|7|7|8|7|0|6
              -----------------
(2,3)->(7,7)  1|5|8|7|7|8|7|0|6
              -----------------
(3,6)->(7,7)  1|5|8|7|7|8|7|0|6
              -----------------
(4,5)->(7,7)  1|5|8|7|7|8|7|0|6
#=====================================
#=====================================
#由parent数组建立的最小生成树             
 0 > 1 > 5 > 8 > 6 > 7 < 4
             ^       ^
             2       3