n皇后（单个解） 马周游问题 回溯法 分治法

##备注：这次有六道题目，所以分成三次来写题目
这两题都涉及到了剪枝法加回溯法，这次题目比较难，我也不太懂其实，讲的不好附上我在网上找到的优秀解析的链接，建议看别人的解析好点。
第一次：https://blog.csdn.net/lil_junko/article/details/92759922
第二次：https://blog.csdn.net/lil_junko/article/details/92759977

题目（1）

时间限制: 1000 ms 内存限制: 64 MB 代码长度限制: 16 KB
给定一个n×n的棋盘和n个皇后，要求在棋盘上放置n个皇后使得任意两皇后的位置满足不同行、不同列且不在同一条对角线（斜率为45度或135度的直线）上，这样的放置位置构成问题的一个解。现约定第1个皇后放置在棋盘的第1行、第2个皇后放置在棋盘的第2行、… 、第n个皇后放置在棋盘的第n行。下图是n=8的情形。因此，n个皇后的一种放置位置可用每个皇后放置位置的列号序列来表示。要求快速给出n皇后问题的一个解。
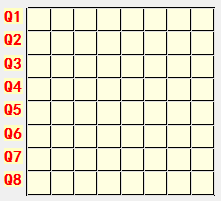输入格式: 输入为在一行中给出一个正整数n(8≤n≤100)。
输出格式: 对每一个输入n，在一行中输出问题的一个解（即这n个皇后放置位置的列号序列）。如果问题有多个解，输出任意一个解即可；如果问题没有解，则输出0。
输入样例: 8
输出样例: 4 6 8 2 7 1 3 5

简单解析

他人的优秀解答：https://www.cnblogs.com/fstang/archive/2013/05/12/3073598.html
1.用随机的思想初始化放置结果（随机找到其中一个位置才开始删枝）。
2.处于同一对角线的位置进行标记，如点C(u,v) ， u+v 和 |u-r| 这两个方向进行标记，这样可以快速查找是否满足所有对角线不存在两个皇后（详情可见《算法竞赛入门经典第二版》刘汝佳著的P193）
3.在根据上面的一步步调整解，直至没有冲突（指存在两个皇后能互相攻击的情况）
（但是为什么这样可以迭代步数变成这么少，也没有解释，如果有证明的方法或者过程，请麻烦发我一份，谢谢）

代码

#include 
#include 
#include 
#define MAX 1000 //最多可能皇后数
#define swap(a,b) {int t = a; a = b; b = t;}
//row[i]表示当前摆放方式下第i行的皇后数，col[i]表示当前摆放方式下第i列的皇后数
int row[MAX];
int col[MAX];

int N; //放置N个皇后在N*N棋盘上

//从左上到右下的对角线上row-col值是相同的，但是这个值有可能是负值，最小为-(N-1)，
//所以可以做个偏移，统一加上N-1，这样这个值就在[0,2*N-2]范围内，将这个值作为该对角线的编号
//pdiag[i]表示当前摆放方式下编号为i的对角线上的皇后数
int pdiag[2 * MAX];//principal diagonal,主对角线，左上到右下（表示和主对角线平行的2N-1条对角线）

//从右上到左下的对角线row+col的值相同，取值范围为[0, 2 * MAX - 2]，作为对角线编号
//cdiag[i]表示编号为i的对角线上的皇后数
int cdiag[2 * MAX];//counter diagonal,副对角线

//R[]用来存储皇后放置位置，R[row] = col表示(row,col)处,即“第row行第col列”有个皇后
int R[MAX];

//给定二维矩阵的一个点坐标，返回其对应的左上到右下的对角线编号
int getP(int row, int col) {
    return row - col + N - 1;
}

//给定二维矩阵的一个点坐标，返回其对应的右上到左下的对角线编号
int getC(int row, int col) {
    return row + col;
}

//返回begin, begin + 1, ... , end - 1 这end - begin个数中的随机的一个
int my_rand(int begin, int end) {//左闭右开[begin, end)
    return rand() % (end - begin) + begin;
}

//原地shuffle算法，算法导论中的randomize in place算法
void randomize(int a[], int begin, int end)// 左闭右开
{
    for(int i = begin; i <= end - 2; i++){
        int x = my_rand(i, end);
        swap(a[i], a[x]);
    }
}

//初始化皇后的摆放，同时初始化row,col,pdiag,cdiag数组
void init()
{
    for(int i = 0; i < N; i++){//N queens
        R[i] = i;
    }
    randomize(R, 0, N);//初始化N个皇后对应的R数组为0~N-1的一个排列，即没有任意皇后同列，也没有任何皇后同行
    for(int i = 0; i < N; i++){
        row[i] = 1;//每行恰好一个皇后
        col[i] = 0;
    }
    for(int i = 0; i < 2 * N - 1; i++){//N queens
        pdiag[i] = 0;
        cdiag[i] = 0;
    }
    for(int i = 0; i < N; i++){//N queens
        col[R[i]]++;
        pdiag[getP(i, R[i])]++;
        cdiag[getC(i, R[i])]++;
    }
}

bool adjust_row(int row);
void print_result();
bool qualify();

int main(int argc, const char *argv[])
{
    srand((unsigned)time(NULL));
    scanf("%d", &N);
    init();
    if (qualify()) {//运气很好，初始化后就满足终止条件
        print_result();
        return 0;
    }
    bool can_terminate = false;
    while (!can_terminate) {
        for (int i = 0; i < N; i++) {
            if(adjust_row(i)) {
                can_terminate = true;
                break;
            }
        }
    }
    print_result();
    return 0;
}
//用最小冲突算法调整第row行的皇后的位置（初始化时每行都有一个皇后，调整后仍然在第row行）
//调整过后check一下看看是否已经没有冲突，如果没有冲突（达到终止状态），返回true
bool adjust_row(int row) {
    int cur_col = R[row];
    int optimal_col = cur_col;//最佳列号，设置为当前列，然后更新
    int    min_conflict = col[optimal_col] + pdiag[getP(row, optimal_col)] - 1
        + cdiag[getC(row, optimal_col)] - 1;//对角线冲突数为当前对角线皇后数减一
    for (int i = 0; i < N; i++) {//逐个检查第row行的每个位置
        if (i == cur_col) {
            continue;
        }
        int conflict = col[i] + pdiag[getP(row, i)] + cdiag[getC(row, i)];
        if (conflict < min_conflict) {
            min_conflict = conflict;
            optimal_col = i;
        }
    }
    if (optimal_col != cur_col) {//要更新col,pdiag,cdiag
        col[cur_col]--;
        pdiag[getP(row, cur_col)]--;
        cdiag[getC(row, cur_col)]--;

        col[optimal_col]++;
        pdiag[getP(row, optimal_col)]++;
        cdiag[getC(row, optimal_col)]++;
        R[row] = optimal_col;
        if (col[cur_col] == 1 && col[optimal_col] == 1 
                && pdiag[getP(row, optimal_col)] == 1 && cdiag[getC(row, optimal_col)] == 1) {
            return qualify();//qualify相对更耗时，所以只在满足上面基本条件后才检查
        }
    }
    //当前点就是最佳点，一切都保持不变
    return false;//如果都没变的话，肯定不满足终止条件，否则上一次就应该返回true并终止了
    //return qualify();
}
bool qualify() {
    for(int i = 0; i < N; i++){//N queens
        if(col[R[i]] != 1 ||
                pdiag[getP(i, R[i])] != 1 ||
                cdiag[getC(i, R[i])] != 1) {
            return false;
        }
    }
    return true;
}
void print_result()
{
    for(int i = 0; i < N; i++){
        printf("%d ", R[i] + 1);
    }
}

题目（2）

时间限制: 1200 ms 内存限制: 64 MB 代码长度限制: 16 KB
任给大小为n×n(8≤n≤1000)的棋盘， 在棋盘上任意设定马的初始位置，试快速找出一种马能跳到每个棋格恰好一次的棋步（要求最后回到初始位置）。注意，棋盘上马按照跳“日”的规则移动。例如，在8×8的棋盘， 当马位于第3行第4列的方格时，下一步可以跳到箭头所指的八个方格之一。
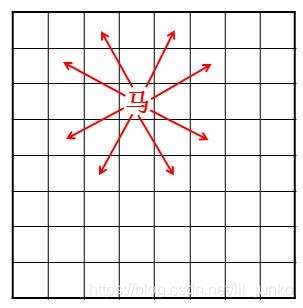输入格式: 在一行中给出三个正整数n,a,b，其中n(8≤n≤1000)为棋盘的行列大小, a和b(1≤a,b≤n)分别是马的初始位置所在方格的行号和列号。
输出格式: 输出占n行，每行含有n个正整数，组成一个n× n方阵。该方阵的n​2​​个元素由正整数1,2,…,n​2​​组成，其中马走第i步前所处方格其内对应的数为i(i=1,2,…,n​2​​) (马在初始位置所处方格内数为1）。
输入样例: 8 3 4
输出样例:
54 57 44 25 64 59 42 9
45 2 55 58 43 8 63 60
56 53 24 1 26 61 10 41
3 46 19 28 21 12 7 62
52 29 4 23 6 27 40 11
47 18 49 20 13 22 37 34
30 51 16 5 32 35 14 39
17 48 31 50 15 38 33 36

简单分析

他人的优秀解答：
https://blog.csdn.net/yuanyirui/article/details/3892583
https://blog.csdn.net/qq_38882906/article/details/80959816

1. 这是找一条哈密顿回路（指定的起点前往指定的终点，途中经过所有其他节点且只经过一次。）
2. 因为马只能走“日”字，每移动一次棋子，(x+y)%2都会进行改变，所以如果能回去的话，棋盘大小必定为偶数
3. 通过链接中的特殊解的方法，运用分治法把大规模的解划分成小规模的问题，下面附上别人的逻辑图：
   单块棋盘满足下面的图片
   
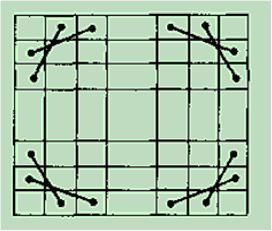
   则四块棋盘可以依靠下述的方法调整为一整块棋盘
   
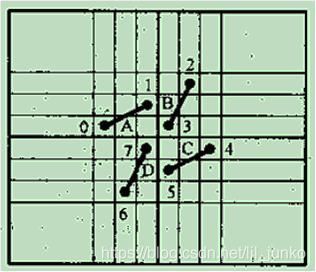
   4.通过重排原理，选择分支数量少的点开始跳，能更快的得到小规模的棋盘的哈密顿回路，再用数组来保存这些路径到程序中，提前计算好避免路径的运算来加快时间。

代码

#include 
#include 
#include 
using namespace std;
//下面代表对于规模的大小的棋盘的路径，其中保存来回路径方便遍历
//保存的数字代表下一步的方向，8种方向用8个数字代表
int ans6_6[6][6][2] = {
{{3,4},{4,5},{3,6},{6,3},{4,6},{5,6}},
{{2,3},{5,2},{2,7},{2,4},{5,7},{7,6}},
{{1,4},{8,3},{7,8},{2,3},{4,1},{5,8}},
{{4,1},{5,4},{6,3},{7,1},{8,4},{7,5}},
{{3,2},{8,3},{3,6},{3,6},{7,1},{6,8}},
{{2,1},{2,8},{8,7},{7,2},{1,7},{8,7}}};
int ans6_8[6][8][2] = {
{{3,4},{3,5},{6,3},{6,3},{3,5},{5,3},{6,4},{6,5}},
{{3,2},{5,2},{5,7},{3,7},{7,2},{7,2},{4,7},{7,6}},
{{1,4},{8,3},{4,7},{1,4},{4,1},{2,7},{1,4},{8,5}},
{{4,1},{5,1},{6,5},{7,5},{5,6},{5,4},{6,4},{5,8}},
{{3,2},{8,3},{2,6},{3,8},{8,2},{3,8},{1,6},{8,6}},
{{2,1},{1,8},{1,7},{7,1},{2,1},{2,7},{8,1},{8,7}}};
int ans8_8[8][8][2] = {
{{3,4},{4,5},{6,4},{3,6},{4,6},{6,3},{4,6},{5,6}},
{{4,2},{2,5},{2,7},{5,2},{2,5},{2,7},{4,5},{7,6}},
{{1,4},{8,5},{6,8},{8,4},{4,3},{2,8},{4,1},{5,8}},
{{1,2},{4,8},{4,1},{1,3},{6,5},{1,3},{7,4},{5,8}},
{{1,4},{8,5},{6,2},{3,4},{8,5},{7,8},{4,1},{7,8}},
{{4,2},{4,5},{3,8},{1,8},{3,4},{4,7},{4,1},{8,5}},
{{1,3},{8,3},{6,3},{1,6},{8,7},{6,3},{6,7},{6,8}},
{{1,2},{2,8},{7,8},{7,2},{7,2},{8,2},{1,8},{7,8}}};
int ans8_10[8][10][2] = {
{{3,4},{3,5},{6,3},{3,6},{3,6},{5,6},{6,3},{3,6},{4,6},{5,6}},
{{3,2},{2,5},{2,7},{2,7},{7,2},{2,7},{2,7},{2,3},{7,4},{5,7}},
{{1,3},{8,5},{5,7},{5,6},{3,1},{3,5},{4,6},{5,4},{4,1},{7,8}},
{{1,4},{2,4},{7,4},{5,3},{2,4},{4,6},{3,7},{6,7},{4,1},{8,6}},
{{1,4},{5,1},{6,1},{2,4},{1,3},{7,2},{6,1},{2,8},{8,7},{5,8}},
{{4,2},{8,5},{8,1},{8,5},{4,2},{8,6},{7,8},{3,4},{6,4},{5,8}},
{{3,1},{8,3},{6,3},{2,6},{8,3},{6,3},{6,2},{3,6},{6,1},{6,7}},
{{1,2},{2,8},{1,7},{7,2},{7,2},{2,8},{7,2},{7,2},{8,1},{8,7}}};
int ans10_10[10][10][2] = {
{{3,4},{3,5},{4,6},{5,3},{3,6},{5,6},{4,6},{6,3},{4,6},{5,6}},
{{2,3},{5,3},{2,7},{2,7},{2,4},{7,2},{2,7},{2,3},{4,5},{7,5}},
{{1,3},{8,5},{7,1},{7,8},{3,1},{6,5},{4,5},{5,8},{4,1},{7,8}},
{{3,1},{4,5},{7,5},{4,2},{4,3},{8,3},{3,7},{1,5},{1,4},{5,8}},
{{1,4},{3,4},{6,7},{4,3},{1,5},{1,4},{7,1},{7,8},{5,7},{5,8}},
{{1,2},{1,5},{6,8},{4,7},{6,8},{7,8},{1,5},{5,6},{5,1},{8,6}},
{{4,2},{8,5},{8,2},{1,6},{4,8},{2,6},{8,6},{2,1},{4,1},{5,6}},
{{1,4},{2,5},{5,4},{2,6},{2,8},{1,6},{5,1},{2,1},{4,5},{5,6}},
{{1,3},{2,8},{6,3},{2,3},{6,3},{6,8},{6,3},{2,3},{6,1},{6,8}},
{{1,2},{8,1},{7,2},{8,2},{7,2},{7,1},{7,2},{1,2},{7,1},{7,8}}};
int ans10_12[10][12][2] = {
{{3,4},{3,5},{5,6},{3,6},{4,5},{3,6},{4,6},{3,6},{3,5},{3,6},{4,5},{5,6}},
{{2,4},{2,5},{6,7},{2,7},{2,5},{2,7},{5,6},{2,7},{4,5},{2,7},{4,7},{5,7}},
{{1,2},{8,1},{6,5},{1,5},{2,3},{6,8},{5,4},{1,8},{6,4},{1,3},{4,1},{5,8}},
{{1,2},{8,5},{4,3},{1,2},{6,3},{6,1},{7,2},{1,6},{6,4},{5,8},{4,1},{7,8}},
{{3,4},{1,5},{1,2},{4,2},{7,3},{2,1},{7,2},{8,6},{3,5},{8,6},{4,1},{5,8}},
{{1,3},{3,4},{6,7},{5,8},{3,5},{2,5},{7,6},{2,5},{4,1},{8,5},{6,7},{5,8}},
{{1,2},{8,5},{7,6},{4,7},{2,8},{3,5},{6,7},{1,3},{6,2},{3,4},{4,1},{5,8}},
{{2,4},{4,5},{8,1},{1,6},{1,2},{5,4},{1,2},{4,7},{1,6},{7,8},{4,1},{5,7}},
{{1,3},{2,3},{6,3},{6,3},{1,8},{6,3},{2,3},{6,3},{6,3},{6,3},{8,1},{6,8}},
{{1,2},{8,2},{7,8},{7,2},{7,1},{7,2},{8,2},{7,2},{7,8},{7,2},{7,1},{7,8}}};
//ceshi数组储存棋盘的往下走的方向变量，sign作为标记数组作为调转的中间变量
//answer数组存储由ceshi数组转换为的顺序数组
int ceshi[1005][1005], sign[1005][1005];
int answer[1005][1005];
//cheng_area输入x,y的范围，用来调转矩阵的方向
void change_area(int x_low, int x_high, int y_low, int y_high)
{
    for(int tmpa = x_low; tmpa <= x_high; tmpa++)
        for(int tmpb = y_low; tmpb <= y_high;tmpb++)
        {
        if(ceshi[tmpa][tmpb] == 1)
            sign[tmpa - 2][tmpb + 1] = 5;
        if(ceshi[tmpa][tmpb] == 2)
            sign[tmpa - 1][tmpb + 2] = 6;
        if(ceshi[tmpa][tmpb] == 3)
            sign[tmpa + 1][tmpb + 2] = 7;
        if(ceshi[tmpa][tmpb] == 4)
            sign[tmpa + 2][tmpb + 1] = 8;
        if(ceshi[tmpa][tmpb] == 5)
            sign[tmpa + 2][tmpb - 1] = 1;
        if(ceshi[tmpa][tmpb] == 6)
            sign[tmpa + 1][tmpb - 2] = 2;
        if(ceshi[tmpa][tmpb] == 7)
            sign[tmpa - 1][tmpb - 2] = 3;
        if(ceshi[tmpa][tmpb] == 8)
            sign[tmpa - 2][tmpb - 1] = 4;
        }
    for(int tmpa = x_low; tmpa <= x_high; tmpa++)
        for(int tmpb = y_low; tmpb <= y_high;tmpb++)
            ceshi[tmpa][tmpb] = sign[tmpa][tmpb];
}
//找到与其对应的数组将方向填入ceshi数组中
void marry(int x_low, int x_high, int y_low, int y_high)
{
    int x_dif = x_high - x_low + 1;
    int y_dif = y_high - y_low + 1;
    if(x_dif == 6)
        if(y_dif == 6)
        {
            for(int tmpa = x_low; tmpa <= x_high; tmpa++)
                for(int tmpb = y_low; tmpb <= y_high; tmpb++)
                    ceshi[tmpa][tmpb] = ans6_6[tmpa - x_low][tmpb - y_low][0];
        }
        else if(y_dif == 8)
        {
            for(int tmpa = x_low; tmpa <= x_high; tmpa++)
                for(int tmpb = y_low; tmpb <= y_high; tmpb++)
                    ceshi[tmpa][tmpb] = ans6_8[tmpa - x_low][tmpb - y_low][0];
        }
    if(x_dif == 8)
        if(y_dif == 6)
        {
            for(int tmpa = 0; tmpa <= x_high - x_low; tmpa++)
                for(int tmpb = 0; tmpb <= y_high - y_low; tmpb++)
                {
                    ceshi[x_low + tmpa][y_high - tmpb] = ans6_8[tmpb][tmpa][0] + 2;
                    if(ceshi[x_low + tmpa][y_high - tmpb] > 8)
                        ceshi[x_low + tmpa][y_high - tmpb] -= 8;
                }
        }
        else if(y_dif == 8)
        {
            for(int tmpa = x_low; tmpa <= x_high; tmpa++)
                for(int tmpb = y_low; tmpb <= y_high; tmpb++)
                    ceshi[tmpa][tmpb] = ans8_8[tmpa - x_low][tmpb - y_low][0];
        }
        else if(y_dif == 10)
        {
            for(int tmpa = x_low; tmpa <= x_high; tmpa++)
                for(int tmpb = y_low; tmpb <= y_high; tmpb++)
                    ceshi[tmpa][tmpb] = ans8_10[tmpa - x_low][tmpb - y_low][0];
        }
    if(x_dif == 10)
        if(y_dif == 8)
        {
            for(int tmpa = 0; tmpa < x_dif; tmpa++)
                for(int tmpb = 0; tmpb < y_dif; tmpb++)
                {
                    ceshi[x_low + tmpa][y_high - tmpb] = ans8_10[tmpb][tmpa][0] + 2;
                    if(ceshi[x_low + tmpa][y_high - tmpb] > 8)
                        ceshi[x_low + tmpa][y_high - tmpb] -= 8;
                }
        }
        else if(y_dif == 10)
        {
            for(int tmpa = x_low; tmpa <= x_high; tmpa++)
                for(int tmpb = y_low; tmpb <= y_high; tmpb++)
                    ceshi[tmpa][tmpb] = ans10_10[tmpa - x_low][tmpb - y_low][0];
        }
        else if(y_dif == 12)
        {
            for(int tmpa = x_low; tmpa <= x_high; tmpa++)
                for(int tmpb = y_low; tmpb <= y_high; tmpb++)
                    ceshi[tmpa][tmpb] = ans10_12[tmpa - x_low][tmpb - y_low][0];
        }
    if(x_dif == 12)
        if(y_dif == 10)
        {
            for(int tmpa = 0; tmpa < x_dif; tmpa++)  //12
                for(int tmpb = 0; tmpb < y_dif; tmpb++)  //10
                {
                    ceshi[x_low + tmpa][y_high - tmpb] = ans10_12[tmpb][tmpa][0] + 2;
                    if(ceshi[x_low + tmpa][y_high - tmpb] > 8)
                        ceshi[x_low + tmpa][y_high - tmpb] -= 8;
                }
        }
}
//分治，将棋盘规模大的划分成小的
void dp(int x_low, int x_high, int y_low, int y_high)
{
    int x_dif = x_high - x_low + 1;
    int y_dif = y_high - y_low + 1;
    //若长和宽之和大于22，则需要分治成四份小的棋盘进行计算
    if(y_dif + x_dif <= 22)
    {
        marry(x_low,x_high,y_low,y_high);
        return;
    }
    int x_mid, y_mid;
    if(x_dif % 4 == 0)
        x_mid = x_low + x_dif/2;
    else
        x_mid = x_low + x_dif/2 + 1;
    if(y_dif % 4 == 0)
        y_mid = y_low + y_dif/2;
    else
        y_mid = y_low + y_dif/2 + 1;
    dp(x_low, x_mid - 1, y_low, y_mid - 1);
    dp(x_low, x_mid - 1, y_mid, y_high);
    dp(x_mid, x_high, y_low, y_mid - 1);
    dp(x_mid, x_high, y_mid, y_high);
    //将四块棋盘调整方向，让他们可以和上面的图一样可以结合到一起
    if(ceshi[x_mid - 2][y_mid - 1] != 6)
        change_area(x_low, x_mid - 1, y_low, y_mid - 1);
    if(ceshi[x_mid - 1][y_mid] != 1)
        change_area(x_low, x_mid - 1, y_mid, y_high);
    if(ceshi[x_mid + 1][y_mid] != 2)
        change_area(x_mid, x_high, y_mid, y_high);
    if(ceshi[x_mid][y_mid - 1] != 5)
        change_area(x_mid, x_high, y_low, y_mid - 1);
    //四块棋盘互相连接
    ceshi[x_mid - 2][y_mid - 1] = 2;
    ceshi[x_mid - 1][y_mid] = 3;
    ceshi[x_mid + 1][y_mid] = 6;
    ceshi[x_mid][y_mid - 1] = 7;
}
//由存储方向的棋盘数组，逐步转换为遍历顺序的answer数组
void zhuanhuan(int a, int b,int step)
{
    while(answer[a][b] == 0)
    {
        step++;
        answer[a][b] = step;
        if(ceshi[a][b] == 1)
        {
            a -= 2;
            b += 1;
        }
        else if(ceshi[a][b] == 2)
        {
            a -= 1;
            b += 2;
        }
        else if(ceshi[a][b] == 3)
        {
            a += 1;
            b += 2;
        }
        else if(ceshi[a][b] == 4)
        {
            a += 2;
            b += 1;
        }
        else if(ceshi[a][b] == 5)
        {
            a += 2;
            b -= 1;
        }
        else if(ceshi[a][b] == 6)
        {
            a += 1;
            b -= 2;
        }
        else if(ceshi[a][b] == 7)
        {
            a -= 1;
            b -= 2;
        }
        else if(ceshi[a][b] == 8)
        {
            a -= 2;
            b -= 1;
        }
    }
}
int main()
{
    //取消关联加速输出
    std::ios::sync_with_stdio(false);
    //初始化数组
    for(int tmp = 0; tmp < 1000; tmp++)
    {
        memset(answer[tmp],0,sizeof(answer[tmp]));
        memset(ceshi[tmp],0,sizeof(ceshi[tmp]));
    }
    int length, x_len, y_len;
    cin >> length >> x_len >> y_len;
    length--;
    dp(0,length, 0,length);
    zhuanhuan(x_len - 1, y_len - 1,0);
    for(int tmpa = 0; tmpa <= length; tmpa++)
    {
        for(int tmpb = 0; tmpb <= length; tmpb++)
            cout <<  answer[tmpa][tmpb] << " ";
        cout <

小声讲一句， 我自己都看不懂自己的代码