算法-手动推演八皇后问题-python3递归实现

0.摘要

本文介绍八皇后问题的解决思路，并使用python3实现。

 

1.问题阐述

目标： 8×8 的国际象棋棋盘上放置八个皇后

规则：任两个皇后都不能处于同一条横行、纵行或斜线上

显然可知：

• 由于任意皇后不能同行，所以每一行最多放置一位皇后；
• 由于行数=皇后数，所以每一行至少放置一位皇后

故：正确的放置方式，一定是每行有且只有一位皇后（1）

为了方便读者了解规则，我们先以4皇后问题为例，推演出可行的解题思路。

本文以图示的方式进行说明，当一个皇后确定位置后，她的同行、同列、同斜线方向不可以再放置其他皇后。

不能放置皇后的位置，我们用灰色表示。

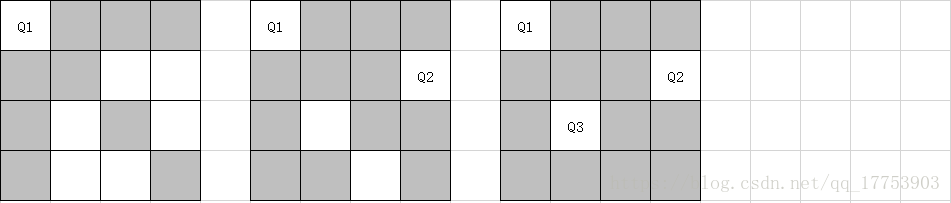
step1：放置第一位皇后：现将第一为皇后放在第一列，那么其同一条横行、纵行或斜线位置将不能再放置其她皇后；

step2：放置第二位皇后：第二位皇后只可以放置在第三列或第四列，先尝试放置在第三列；

step3：放置第三位皇后：由于第三行所有位置都无法放置第三位皇后，这与上文（1）出给出的结论相悖，故该放置方式不合理。

重复上述分析过程，可知，无法正确放置第四位皇后，故该方法亦不可行；

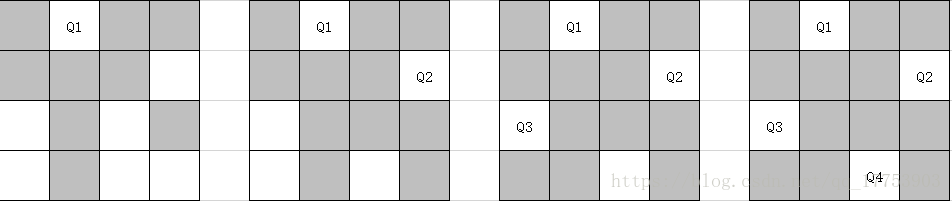
 通过图示方法，我们发现所有皇后都正确放置，因此我们得到了第一种解法。

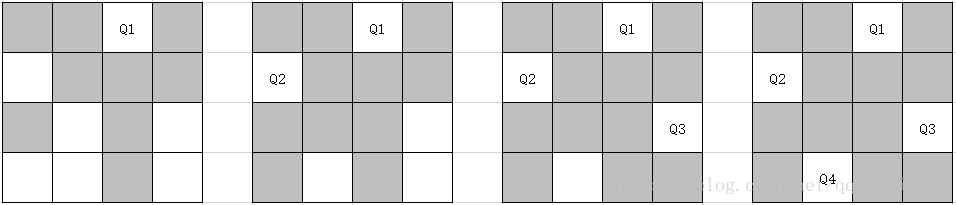
继续改变Q1的位置，我们得到了第二种解法。

这时候，我们仔细观察一下，发现第一种和第二种解法是完全对称的！

继续思考一下易得，N皇后问题，当N=偶数时，其解法个数必将是偶数。

 

2.解题思路

通过上一节对四皇后问题的手动推演，我们可以将问题分为三个子问题：

• 每一行必定有且只有一位皇后。因此，我们只要确定的是，每一行的皇后所处列数。
• 确定一位皇后，其同行、同列、同斜线位置不能再放置其他皇后。标记处这些位置，才能减少需要遍历的状态，从而减小运算量。
• 需要将遍历的步骤抽象成可递归的操作。

我们知道，是否在同行同列，只需要根据行数和列数的下表即可判断；

那同斜线方向的位置，如何判定？

简单的方式，仍然是遍历，判断y1-y2 == x1-x2是否成立即可。但如果每个位置都要先遍历一遍位置阵列，这样的方法计算量太大。是否有更加简单的方法呢？请读者看下面两端代码：

def left_diagonal(n):
    arr = [[0 for _ in range(n)] for _ in range(n)]
    for i in range(n):
        for j in range(n):
            arr[i][j] = i + j
    return arr

if __name__ == '__main__':
    arr = left_diagonal(8)
    for a in arr:
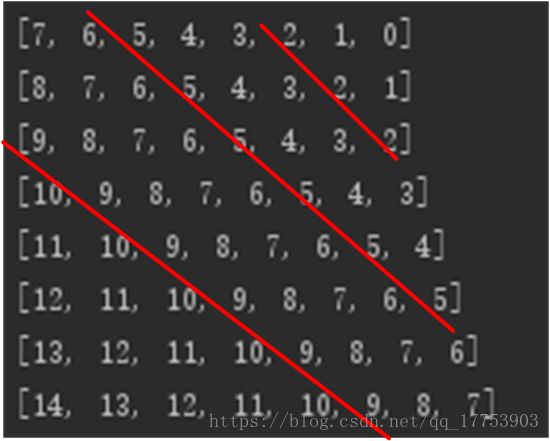
        print(a)

程序运行后的结果为： 

 

可见，每一个位置的行列值相加，同一左斜线上的和都相等。

这就表明，我们如果想要判定两个元素是否在同一条左斜线上，将其行列值相加，观察和是否相等即可。

并且，这样的斜边共有15条。

在看另外一个程序：

def left_diagonal(n):
    arr = [[0 for _ in range(n)] for _ in range(n)]
    for i in range(n):
        for j in range(n):
            arr[i][j] = i + j
    return arr

def right_diagonal(n):
    arr = [[0 for _ in range(n)] for _ in range(n)]
    for i in range(n):
        for j in range(n):
            arr[i][j] = i - j + (n - 1)
    return arr

if __name__ == '__main__':
    arr = right_diagonal(8)
    for a in arr:
        print(a)

运行结果：

可见，每一个位置的行列值的差，同一右斜线上的和都相等。

这就表明，我们如果想要判定两个元素是否在同一条右斜线上，将其行列值相减，观察和是否相等即可。

同样，右斜线也有15条。

 

3.使用递归解决八皇后问题：

先看代码

#coding=utf-8

num = 8
result = [-1 for _ in range(num)]
enable0 = [True for _ in range(num)]
enable1 = [True for _ in range(2*num-1)]
enable2 = [True for _ in range(2*num-1)]
result = [-1 for _ in range(num)]
out_list = []

def queen(r):
    if (r == 8):
        # print(result)
        out_list.append(result.copy())
        return 0
    else:
        for c in range(num):
            if (enable0[c] and enable1[r+c] and enable2[r-c+num-1]):
                enable0[c] = False
                enable1[r+c] = False
                enable2[r-c+num-1] = False
                result[r] = c
                queen(r+1)
                result[r] = -1
                enable0[c] = True
                enable1[r + c] = True
                enable2[r - c + num-1] = True

queen(0)
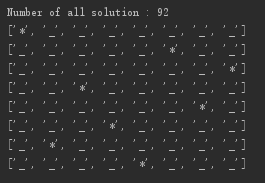
print('Number of all solution :',len(out_list))
one_solution = out_list[1]
for index in one_solution:
    temp = ['_' for _ in range(8)]
    temp[index] = '*'
    print(temp)

本代码，通过设置三个辅助数组，enable0，enable1,enalbe2分别表示8列、15条左斜线，15条右斜线的位置可用状态。

通过递归，可以实现所有情况的遍历。

结果:

最终，程序得到了92中解法，并对其中一种做了展示。