最短路上的统计（Floyed-Warshall算法）

如果还不是很清楚Floyed-Warshall算法的大佬们请去看一看本蒟蒻的Floyed算法博客，链接：

blog.csdn.net/qq_41735385/article/details/86705022

Problem: 最短路上的统计

Time Limit: 1 Sec Memory Limit: 128 MB

Description

一个无向图上，没有自环，所有边的权值均为1，对于一个点对（a,b）
我们要把所有a与b之间所有最短路上的点的总个数输出。

Input

第一行n,m,表示n个点，m条边
接下来m行，每行两个数a,b,表示a,b之间有条边
在下来一个数p,表示问题的个数
接下来p行，每行两个数a,b,表示询问a,b
n<=100，p<=5000

Output

对于每个询问，输出一个数c,表示a,b之间最短路上点的总个数

Sample Input

5 6
1 2
1 3
2 3
2 4
3 5
4 5
3
2 5
5 1
2 4

Sample Output

4//对于第一个询问有2,3,4,5这四个点
3
2

HINT

题目分析：

1.题目大意

本题就是说给我们一个无向图，再p次访问，让我们求每次访问的两点之间，最短路径所经过的点的的总个数。

2.解题思路

本题毫无疑问是最短路问题，而且是无向图，多源的最短路。
所以是妥妥的Floyed-Warshall算法。

But!!!

本题有点特殊，它说的是总个数，也就是说本题的最短路不止一条，而且恶心的是要我们求点的个数！
别慌，我一开始也懵逼，那么我们先看看样例：

Sample Input

5 6
1 2
1 3
2 3
2 4
3 5
4 5
3
2 5
5 1
2 4

Sample Output

4//对于第一个询问有2,3,4,5这四个点
3
2

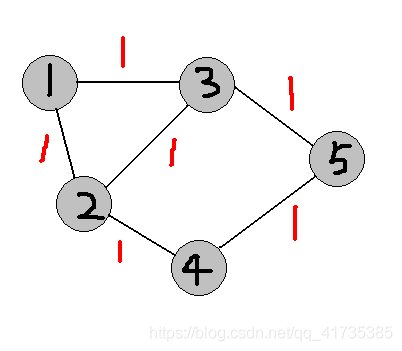
样例1：
2 to 5的最短路：
2–3--5 or 2–4--5
那么有两条，则经过的总点数就是4[2,3,4,5]，完全没问题。
那么样例弄清楚后，到底应该怎么做呢？

步骤：

1.用Floyed-Warshall算法求出最短路，但要注意，这里的每条边权都是1，那么我们易知：

最短距离==最短距离所经过的边的数量

[显然并没有什么用]

2.在每次询问后，都要去暴力枚举(本蒟蒻很蠢真的想不出怎样便捷)，也就是说，从这个算法的根源出发——枚举中转点！具体代码如下：

int ans=2;//注意起始点都算，所以ans赋初值
for (int d=1;d<=n;d++)
	if (d!=a&&d!=b&&w[a][d]+w[d][b]==w[a][b])
		//d!=a&&d!=b是为了防止枚举的中转点与起始点重合
		/*w[a][d]+w[d][b]==w[a][b]这里的意思是:
		  从a to d的最短路与d to 的最短路之和等于a to b的最短路
		  即必为最短路所经过的点
		*/
		ans++;

所以这道题就轻易地AC了。

最终代码：

#include 
#include 
#include 
#pragma GCC optmize(2)
using namespace std;

int n,m,a,b,p;
int w[101][101]; //说明i to j的最短路

bool check(int x,int y,int z)//这里不再赘述
{
	return (x!=y)&&(y!=z)&&(x!=z)&&(w[x][z]+w[z][y]<w[x][y]);
}

inline void read(int &x) //quickly read快读
{
	x=0;int f=1;char c=getchar();
	while (c<'0'||c>'9') {if (c=='-') f=~(f-1);c=getchar();}
	while (c>='0'&&c<='9') x=(x<<1)+(x<<3)+(c^48),c=getchar();
	x*=f;
}

int main()
{
	read(n);read(m);
	for (int i=1;i<=n;i++)
		for (int j=1;j<=n;j++)
			if (i!=j) w[i][j]=101; //i!=j说明不能走到自己这个点
			//给w赋初值，代表仍两点之间都未有路
	for (int i=0;i<m;i++)
	{
		read(a),read(b);
		w[a][b]=w[b][a]=1;
		//注意无向图,a to b与b to a都要赋值为1
		//还要注意这里的1不仅代表a,b之间的距离，也是指边的个数
	}
	for (int d=1;d<=n;d++)
		for (int i=1;i<=n;i++)
			for (int j=1;j<=n;j++)
				if (check(i,j,d))
					w[i][j]=w[i][d]+w[d][j];
	//朴素的Floyed-Warshall算法
	read(p);
	for (int i=0;i<p;i++)
	{
		int ans=2;
		read(a),read(b);
		for (int d=1;d<=n;d++)
			if (d!=a&&d!=b&&w[a][d]+w[d][b]==w[a][b]) ans++;
			//前面已经解释
		printf("%d\n",ans);
	}
	return 0;
}

如有不好之处，还请各位神犇指出来，不吝赐教！