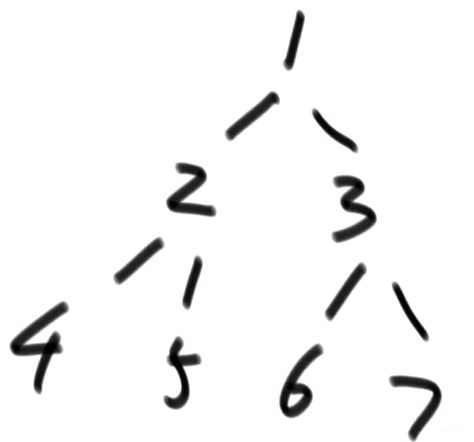数据结构与算法（二）：堆，大根堆，小根堆，堆排序，比较器详解

堆

什么是堆？

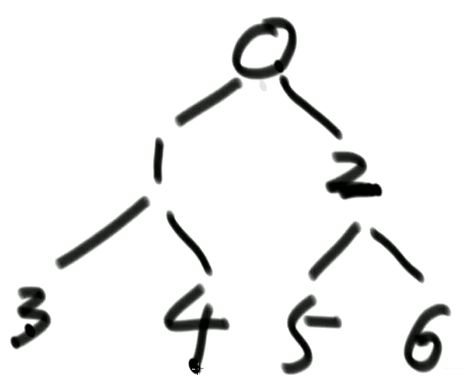
堆 是一棵 完全二叉树：即使它不是满二叉树，也是正在从左往右变满的过程中。

1）堆结构就是用数组实现的完全二叉树结构

2）完全二叉树中，如果每棵子树的 最大值都在顶部，是 大根堆

3）完全二叉树中，如果每棵子树的 最小值都在顶部，是 小根堆

4）堆结构的 heapInsert 与 heapify 操作

5）堆结构的增大和减少

6）优先级队列结构，就是堆结构

7）特点：由 N 个数 组成的堆，高度是 log(n)

如何用数组存放堆？

如果从 0 位置开始：

i 层，则

• 左孩子：2 * i + 1
• 右孩子：2 * i + 2
• 父节点：(i - 1) / 2

如果从 1 位置开始：

正是由于可以使用 位运算 来代替 算数运算，效率更高，所以有时候让下标从 1 开始。

• 左孩子：2 * i （i << 1）
• 右孩子：2 * i + 1 （i << 1 | 1）
• 父节点：i / 2 （i >> 1）

如何将数组转化成大根堆？—— heapInsert 操作

每在 i 位置加入一个新的节点，都与它的 (i - 1) / 2 位置的父节点比较，如果比父节点大，则交换（并while比较父节点与父父节点）

private void heapInsert(int[] arr, int index) {
    while (arr[index] > arr[(index - 1) / 2]) {
        swap(arr, index, (index - 1) / 2);
        index = (index - 1) / 2;
    }
}
private void swap(int[] arr, int i, int j) {
    int tmp = arr[i];
    arr[i] = arr[j];
    arr[j] = tmp;
}

如何返回并删除大根堆的最大值，剩余数字依然保持大根堆？—— heapify 操作

1. 将顶部元素取出
2. 将大根堆的最后位置上的元素覆盖到顶部
3. while 循环
   1. 如果左右孩子中较大的数比当前节点更大，则交换当前节点和较大的孩子节点
   2. 如果左孩子下标越界，或左右孩子都不比当前节点大，就停止

// 返回最大值，并在大根堆中把最大值删掉，剩下的数依然保持大根堆形态
public int pop() {
    int ans = heap[0];
    swap(heap, 0, --heapSize);
    heapify(heap, 0, heapSize);
    return ans;
}
// 从index位置开始，不断的下沉，直到我的孩子都不再比我大，或者我已经没孩子了，就停止
private void heapify(int[] arr, int index, int heapSize) {
    int left = index * 2 + 1;
    while (left < heapSize) {
        // largest存储左右孩子 较大者 的下标
        int largest = left + 1 < heapSize && arr[left + 1] > arr[left] ? left + 1 : left;
        // largest存储两个孩子与父节点 较大者 的下标
        largest = arr[largest] > arr[index] ? largest : index;
        if (largest == index) { // 不需要交换的情况
            break;
        }
        swap(arr, largest, index);
        index = largest;
        left = index * 2 + 1;
    }
}

堆排序

1. 先让整个数组都变成大根堆结构，建立堆的过程:
   1. 从上到下的方法，时间复杂度为O(N*logN)
   2. 从下到上的方法，时间复杂度为O(N)
2. 把堆的最大值和堆末尾的值交换，然后减少堆的大小之后，再去调整堆，一直周而复始，时间复杂度为O(N*logN)
3. 堆的大小减小成0之后，排序完成！

public static void heapSort(int[] arr) {
    if (arr == null || arr.length < 2) {
        return;
    }
    // 方法1：对数组进行堆排序 O(N*logN)
    for (int i = 0; i < arr.length; i++) { // O(N)
        heapInsert(arr, i); // O(logN)
    }
    // 方法2：仅将数组转化成大顶堆 O(n) 
    for (int i = arr.length - 1; i >= 0; i--) {
        heapify(arr, i, arr.length);
    }
}

语言提供的堆结构 vs 手写的堆结构，怎么选择？

取决于你有没有 动态改信息 的需求！

• 语言提供的堆结构，如果你动态改数据，不保证依然有序

• 手写堆结构，因为增加了对象的位置表，所以能够满足动态改信息的 resign 需求（以后我们的 Dijskra 会用到），而系统自带的堆结构即使是实现了对数据的修改，时间复杂度也不会好，因为它没有 hashmap，只能从顶部开始，遍历每个元素进行 heapify

  public static class MyHeap<T> {
      private ArrayList<T> heap;			  	  // 用动态数组存堆
      private HashMap<T, Integer> indexMap; 	  // 对象的位置表
      private int heapSize;	              	  // 堆大小
      private Comparator<? super T> comparator; // 自定义比较器
      
      /*...省略push,pop,heapInsert,heapify等...*/
      public void resign(T value) { // resign操作不需要全量遍历整个堆
         int valueIndex = indexMap.get(value);
         heapInsert(valueIndex); // 这个heapInsert和下面的heapify，只会命中一个，另一个直接返回
         heapify(valueIndex, heapSize);
      }
  }
  public static void main(String[] args) {
      myHeap = new MyHeap<>(new StudentComparator());
  	/*...省略s1, s2等new对象过程...*/
      myHeap.push(s1);
      myHeap.push(s2);
      myHeap.push(s3);
      myHeap.push(s4);
      myHeap.push(s5);
  
      s2.age = 6;
      myHeap.resign(s2);
  }
  

PriorityQueue 底层就是用堆实现的，默认是小根堆

public static void main(String[] args) {
    // 小根堆
    PriorityQueue<Integer> heap = new PriorityQueue<>();
    heap.add(5);
    heap.add(7);
    heap.add(3);
    heap.add(0);
    heap.add(2);
    heap.add(5);
    while (!heap.isEmpty()) { // 排序输出
        System.out.println(heap.poll());
    }
}

与堆有关的题目

已知一个几乎有序的数组。

几乎有序是指，如果把数组排好顺序的话，每个元素移动的距离一定不超过k（假设k=5），并且k相对于数组长度来说是比较小的。

请选择一个合适的排序策略，对这个数组进行排序。

思路：维护一个大小为 k 的小根堆，每加入一个新数字，先将小根堆的最小值弹出，再把新值放入小根堆中去。

public static void sortedArrDistanceLessK(int[] arr, int k) {
    if (k == 0) {
        return;
    }
    // 默认小根堆，复杂度：log(k)
    PriorityQueue<Integer> heap = new PriorityQueue<>();
    int index = 0;
    for (; index <= Math.min(arr.length - 1, k - 1); index++) {
        heap.add(arr[index]);
    }
    int i = 0;
    for (; index < arr.length; i++, index++) {
        heap.add(arr[index]);
        arr[i] = heap.poll();
    }
    while (!heap.isEmpty()) {
        arr[i++] = heap.poll();
    }
}

比较器 Comparator

1)比较器的实质就是重载比较运算符

2)比较器可以很好的应用在特殊标准的排序上

3)比较器可以很好的应用在根据特殊标准排序的结构上

4)写代码变得异常容易，还用于范型编程

public static class IdAscendingComparator implements Comparator<Student> {
    // 返回负数，第一个参数排在前面
    // 返回正数，第二个参数排在前面
    // 返回0的时候，谁在前面无所谓
    @Override
    public int compare(Student o1, Student o2) {
        return o1.id - o2.id;
    }
}
public static void main(String[] args) {
    Student student1 = new Student("A", 2, 20);
    Student student2 = new Student("B", 3, 21);
    Student student3 = new Student("C", 1, 22);
    Student[] students = new Student[]{student1, student2, student3};
    Arrays.sort(students, new IdAscendingComparator());
}

用 Comparator 排序：

public static class HeapComp implements Comparator<Integer> {
    @Override
    public int compare(Integer o1, Integer o2) {
        return o2 - o1;
    }
}
public static void main(String[] args) {
    Integer[] arr = {5, 4, 3, 2, 7, 9, 1, 0};
    Arrays.sort(arr, new HeapComp());
}